Direct limit is a fundamental concept in category theory and algebra that constructs an object capturing the essence of a directed system of structures, such as groups or modules. It allows the coherent assembly of an increasing sequence of objects and morphisms into a single universal object, preserving the directedness of the system. Dive deeper into this article to understand how direct limits function and their applications in various mathematical contexts.
Table of Comparison
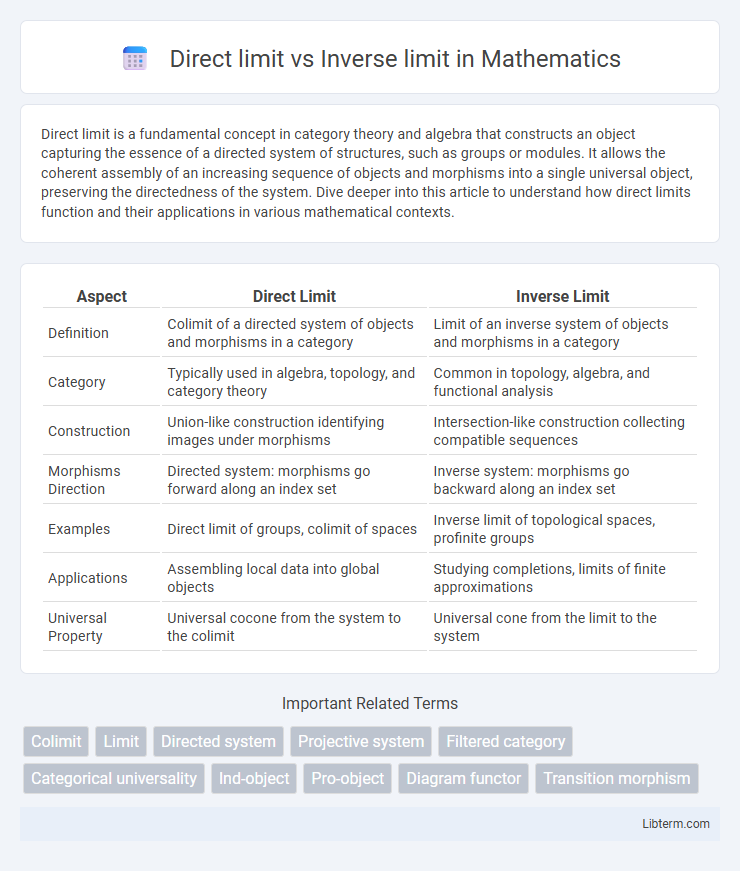
| Aspect | Direct Limit | Inverse Limit |
|---|---|---|
| Definition | Colimit of a directed system of objects and morphisms in a category | Limit of an inverse system of objects and morphisms in a category |
| Category | Typically used in algebra, topology, and category theory | Common in topology, algebra, and functional analysis |
| Construction | Union-like construction identifying images under morphisms | Intersection-like construction collecting compatible sequences |
| Morphisms Direction | Directed system: morphisms go forward along an index set | Inverse system: morphisms go backward along an index set |
| Examples | Direct limit of groups, colimit of spaces | Inverse limit of topological spaces, profinite groups |
| Applications | Assembling local data into global objects | Studying completions, limits of finite approximations |
| Universal Property | Universal cocone from the system to the colimit | Universal cone from the limit to the system |
Introduction to Limits in Mathematics
Direct limits and inverse limits are fundamental concepts in category theory and algebra that describe ways to construct new objects from directed systems of existing ones. Direct limits capture the notion of a "union" or "colimit" by coherently merging objects along morphisms, often used in modules, groups, and topological spaces. In contrast, inverse limits, or projective limits, define an "intersection" or "limit" by taking compatible elements from a family of objects indexed in a reverse direction, playing a crucial role in topology, algebraic geometry, and homological algebra.
Understanding Direct Limits: Definition and Concept
Direct limits, also known as colimits in category theory, describe the process of coherently combining a directed system of objects and morphisms into a single universal object that encapsulates all the data. They are constructed by taking the union or suprema of an increasing sequence of structures, ensuring consistency through compatible morphisms. Understanding direct limits is key in fields like algebra and topology, where they model growth or approximation of objects through directed systems.
Inverse Limits Explained: Fundamentals and Meaning
Inverse limits, also known as projective limits, are a foundational concept in category theory and topology, used to construct an object from a sequence of related objects connected by morphisms directed "backwards." They allow the reconstruction of complex structures as the limit of simpler approximations, preserving compatibility conditions among the connecting maps. Common applications include defining profinite groups, completing rings in algebraic geometry, and studying inverse systems in homological algebra.
Key Differences Between Direct and Inverse Limits
Direct limits, also known as colimits, construct an object by aggregating a directed system of objects and morphisms, typically emphasizing inductive or "limiting upward" processes. Inverse limits, or projective limits, form an object by taking the limit over a system indexed by a directed set with morphisms going "backwards," often focusing on restricting or "limiting downward" sequences. The key differences lie in their construction direction, their categorical duality, and their applications: direct limits assemble objects via colimit processes, while inverse limits capture compatible inverse system elements through limit processes.
Construction of Direct Limits: Step-by-Step
Construction of direct limits involves defining a directed system of objects and morphisms indexed by a directed set. Each object in the system maps consistently into subsequent objects, allowing the formation of a colimit by identifying elements that become equivalent under these morphisms. The direct limit is obtained by taking the disjoint union of all objects and imposing an equivalence relation generated by the morphisms, resulting in a universal object representing the colimit in the category.
Building Inverse Limits: Methodology and Process
Building inverse limits involves constructing an object as the limit of a projective system of spaces or algebraic structures connected by surjective morphisms, emphasizing coherence conditions across the entire system. The methodology requires defining bonding maps that satisfy compatibility relations, ensuring that each stage projects onto the previous one, facilitating the capturing of intricate properties from infinite sequences. This process allows the reconstruction of complex objects from simpler approximations, widely used in topology, category theory, and algebraic geometry to study objects via their finite-level data.
Applications of Direct Limits in Algebra and Topology
Direct limits provide a crucial framework for constructing large algebraic or topological structures from directed systems of smaller, more manageable components, enabling the analysis of inductive systems in categories like groups, modules, and topological spaces. In algebra, direct limits facilitate the study of infinite-dimensional vector spaces, filtered colimits of rings, and the behavior of homology theories, while in topology, they underpin the formation of CW complexes and simplify the handling of increasing sequences of subspaces. This construction streamlines the understanding of continuity, coherence, and completeness properties across diverse mathematical contexts by aggregating local data into a global structure.
Practical Uses of Inverse Limits in Mathematical Structures
Inverse limits are essential in topology and algebra for constructing objects by systematically "gluing" simpler structures along connecting morphisms. They enable analysis of profinite groups, completing rings, and studying spaces by capturing their limiting behavior through projective systems. Practical uses include modeling fractals, formalizing p-adic numbers, and solving problems in shape theory and algebraic geometry.
Common Examples Comparing Direct vs Inverse Limits
Direct limits often appear in algebraic topology when constructing homology groups from a directed system of spaces, such as the colimit of increasing subcomplexes, while inverse limits commonly arise in number theory and algebraic geometry, exemplified by the p-adic integers as the inverse limit of the system of integers modulo p^n. In module theory, the direct limit is used to build larger modules from directed systems, whereas the inverse limit captures projective systems, like profinite groups formed as inverse limits of finite groups. Comparing these, direct limits preserve colimits and approximate objects from below, while inverse limits preserve limits and approximate objects from above, highlighting their dual roles in categorical constructions.
Summary and Importance in Mathematical Theory
Direct limits and inverse limits serve as fundamental tools in category theory and algebra, facilitating the construction and analysis of complex structures by coherently assembling simpler objects. Direct limits capture the union or colimit of a directed system, enabling the study of limits of increasing sequences of spaces or groups, while inverse limits focus on projective systems and provide mechanisms to handle completions and compactifications such as profinite groups. Their importance lies in unifying diverse mathematical concepts, proving existence theorems, and enabling deep insights in topology, algebraic geometry, and homological algebra.
Direct limit Infographic
 libterm.com
libterm.com