Zero is a fundamental concept in mathematics representing the absence of quantity or value, playing a crucial role in arithmetic, algebra, and calculus. It serves as the neutral element in addition and is essential for understanding place value and number systems. Explore the rest of the article to discover how zero shapes mathematical theory and everyday calculations.
Table of Comparison
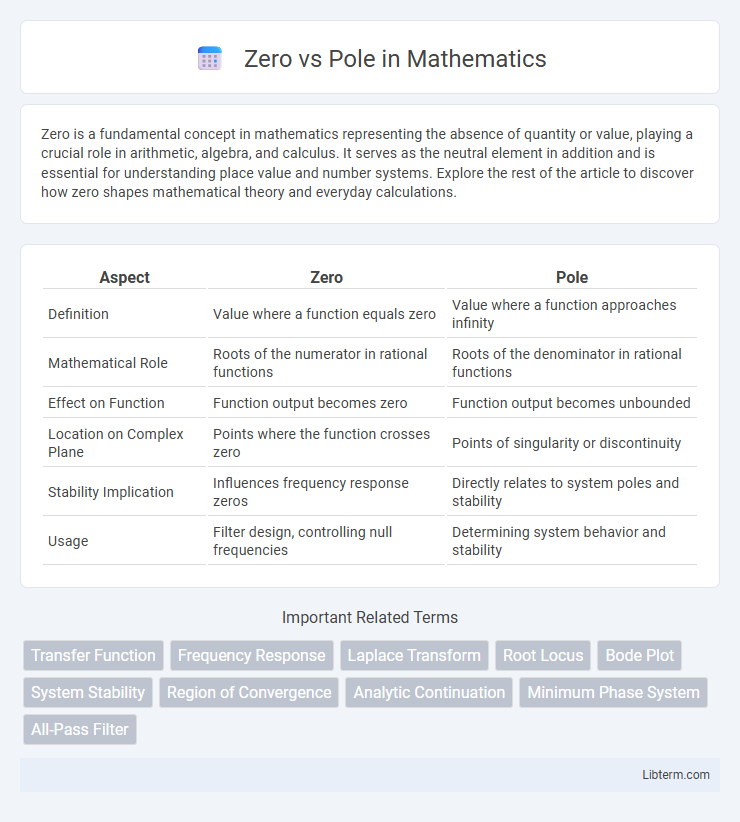
| Aspect | Zero | Pole |
|---|---|---|
| Definition | Value where a function equals zero | Value where a function approaches infinity |
| Mathematical Role | Roots of the numerator in rational functions | Roots of the denominator in rational functions |
| Effect on Function | Function output becomes zero | Function output becomes unbounded |
| Location on Complex Plane | Points where the function crosses zero | Points of singularity or discontinuity |
| Stability Implication | Influences frequency response zeros | Directly relates to system poles and stability |
| Usage | Filter design, controlling null frequencies | Determining system behavior and stability |
Introduction to Zeros and Poles
Zeros and poles are fundamental concepts in control systems and signal processing, representing specific frequencies where a system's transfer function becomes zero or tends toward infinity. Zeros correspond to frequencies that completely attenuate input signals, while poles indicate frequencies that amplify or resonate within the system. Analyzing zeros and poles enables precise understanding of system stability, frequency response, and overall dynamic behavior.
Defining Zeros in Control Systems
Zeros in control systems are specific values of the complex frequency variable where the system's transfer function becomes zero, indicating frequencies that completely cancel out the output. These points play a critical role in shaping the system's frequency response and stability by influencing the root locus and transient behavior. Understanding zeros helps engineers tailor system dynamics to improve performance, reduce overshoot, and achieve desired bandwidth characteristics.
Understanding Poles in System Analysis
Poles are critical points in system analysis where the system's transfer function becomes infinite, significantly influencing stability and dynamic response. Understanding poles helps predict system behavior, such as convergence or oscillations, by determining natural frequencies and damping characteristics. Analyzing pole locations in the complex plane enables engineers to design controllers that ensure desired performance and robustness in control systems.
Mathematical Representation of Zeros and Poles
Zeros are the roots of the numerator polynomial in a transfer function, represented as values of the complex variable z where the function equals zero. Poles are the roots of the denominator polynomial, indicating points of infinite magnitude in the transfer function and dictating system stability. Mathematically, if H(z) = N(z)/D(z), zeros satisfy N(z) = 0 while poles satisfy D(z) = 0, with N(z) and D(z) being polynomials in z.
Physical Significance of Zeros vs Poles
Zeros represent the frequency points where a system's output completely diminishes, indicating signal attenuation or nullification in physical systems such as filters or control circuits. Poles correspond to frequencies where the system's response theoretically approaches infinity, associated with resonant frequencies, instability, or energy amplification in mechanical or electrical domains. Understanding zeros and poles is crucial for designing stable systems with desired frequency responses and ensuring robust performance under varying operational conditions.
Impact on System Stability
Poles determine system stability by their location in the s-plane; poles in the right half-plane indicate instability, while those in the left half-plane ensure stability. Zeros influence transient response and frequency characteristics but do not directly dictate stability. The relative placement of zeros and poles shapes the overall system behavior, affecting damping, oscillations, and steady-state error.
Frequency Response: Zeros vs Poles
Zeros in a frequency response represent frequencies where the output magnitude becomes zero, effectively attenuating those signals and creating notches in the spectrum. Poles correspond to frequencies where the system's gain approaches infinity, leading to resonant peaks and amplifying signals near these frequencies. The interplay between zeros and poles shapes the system's frequency response, determining bandwidth, stability, and filter characteristics such as passband and stopband behavior.
Practical Examples and Applications
Zeros and poles play a crucial role in the design of filters and control systems, where zeros correspond to frequency points that completely attenuate signals, and poles indicate frequencies that amplify or sustain signals indefinitely. In practical applications such as audio equalizers and active filters, strategically placing zeros helps eliminate unwanted noise, while poles are tuned to sharpen frequency selectivity and ensure system stability. Control system engineers use pole-zero plots to predict system behavior, optimize transient response, and avoid instability in robotic motion control and aerospace applications.
Visualization on the Complex Plane
Zeros appear as points on the complex plane where a system's transfer function equals zero, often visualized as circles or crosses, indicating frequency components that are completely attenuated. Poles are represented as distinct points where the transfer function approaches infinity, marked typically with X's, highlighting frequencies that dominate system behavior and stability. Plotting zeros and poles together provides critical insights into system dynamics, resonance, and frequency response characteristics essential for control system analysis and filter design.
Key Differences: Zero vs Pole Summary
Zeros represent the values of a function's variable where the function equals zero, indicating points of signal cancellation in system analysis, while poles correspond to values where the function approaches infinity, reflecting system instability or resonance. Poles dictate system stability and frequency response, often located in the complex plane's left-half for stable systems, whereas zeros shape the output by introducing phase shifts and amplitude changes. Understanding the precise locations and effects of zeros and poles is fundamental in control system design, filter construction, and signal processing for optimizing performance.
Zero Infographic
 libterm.com
libterm.com