First and second category sets play a crucial role in topology and analysis, where first category sets are countable unions of nowhere dense sets, while second category sets are not. Open sets contain neighborhoods around each point, contrasting with closed sets that include all their limit points, and nowhere dense sets are those whose closure has empty interior. Explore the rest of this article to deepen your understanding of these fundamental concepts and their implications in mathematical analysis.
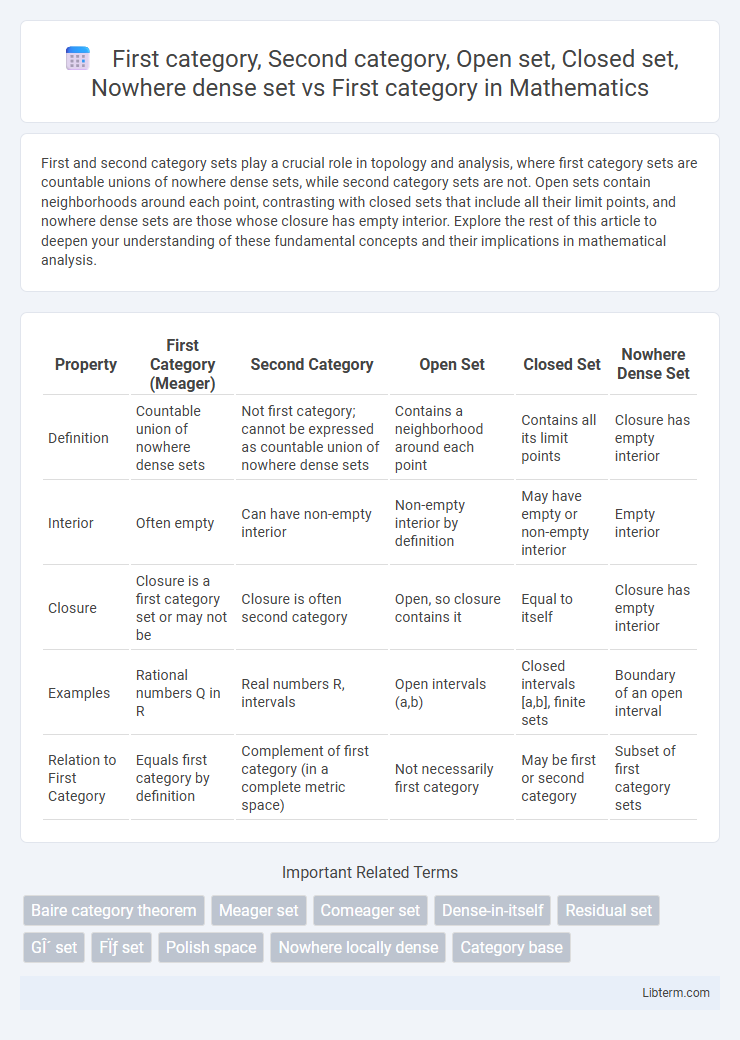
Table of Comparison
| Property | First Category (Meager) | Second Category | Open Set | Closed Set | Nowhere Dense Set |
|---|---|---|---|---|---|
| Definition | Countable union of nowhere dense sets | Not first category; cannot be expressed as countable union of nowhere dense sets | Contains a neighborhood around each point | Contains all its limit points | Closure has empty interior |
| Interior | Often empty | Can have non-empty interior | Non-empty interior by definition | May have empty or non-empty interior | Empty interior |
| Closure | Closure is a first category set or may not be | Closure is often second category | Open, so closure contains it | Equal to itself | Closure has empty interior |
| Examples | Rational numbers Q in R | Real numbers R, intervals | Open intervals (a,b) | Closed intervals [a,b], finite sets | Boundary of an open interval |
| Relation to First Category | Equals first category by definition | Complement of first category (in a complete metric space) | Not necessarily first category | May be first or second category | Subset of first category sets |
Introduction to Set Categorization in Topology
First category sets, also known as meager sets, consist of countable unions of nowhere dense sets, representing "small" or "thin" subsets in topology. In contrast, second category sets are not first category and capture "large" or "robust" subsets within a topological space. The distinction between open and closed sets clarifies topological structure, while nowhere dense sets form the building blocks of first category sets, emphasizing their limited topological size and significance.
Understanding First Category Sets
First category sets, also known as meager sets, consist of countable unions of nowhere dense sets, contrasting with second category sets that are not meager and contain "large" subsets in topological spaces. Closed sets form complete boundaries without gaps, often serving as building blocks for nowhere dense sets, which lack interior points and contribute to the structure of first category sets. Understanding first category sets involves analyzing their negligible measure in Baire category theory, where open sets are dense and second category sets represent "typical" or generic properties in complete metric spaces.
Defining Second Category Sets
Second category sets are defined as sets that are not of the first category, meaning they cannot be represented as a countable union of nowhere dense sets. In a complete metric space, second category sets exhibit "largeness" or "thickness," contrasting with first category sets, which are considered "small" or "meager." Unlike closed sets or open sets, the classification into first or second category depends on the set's topological complexity rather than its openness or closedness.
Exploring Open Sets in Topological Spaces
Open sets in topological spaces serve as the foundational building blocks that define the structure and properties of the space. First category sets, often called meager sets, can be expressed as countable unions of nowhere dense sets, highlighting their small size in a topological sense, whereas second category sets are not meager and possess a richer topological presence. Closed sets, being complements of open sets, interplay with nowhere dense sets to characterize boundary behaviors, and exploring these relationships unveils crucial insights about the openness and closure properties within various topological frameworks.
Characteristics of Closed Sets
Closed sets contain all their limit points, ensuring that sequences converging within the set remain inside it, contrasting with open sets that exclude boundary points. In topological spaces, closed sets complement open sets and are crucial in defining nowhere dense sets, which are subsets whose closure has empty interior. First category sets, also known as meager sets, can be expressed as countable unions of nowhere dense sets, highlighting the interplay between closed sets and the structure of category in topology.
Nowhere Dense Sets: Meaning and Examples
Nowhere dense sets are subsets of a topological space whose closure has an empty interior, meaning they are "thin" and do not contain any open subset. These sets play a crucial role in distinguishing first category (meager) sets, which are countable unions of nowhere dense sets, from second category sets that cannot be so decomposed. Examples of nowhere dense sets include the set of rational numbers within the real numbers and the Cantor set, both of which exemplify intricate structures with empty interior yet significant topological properties.
Comparison: First Category vs. Nowhere Dense Sets
First category sets, also known as meager sets, are countable unions of nowhere dense sets, indicating they are "small" in the sense of Baire category but can be more complex in structure. Nowhere dense sets have closures with empty interiors, making them sparse and lacking any "thick" part in the topological space, while first category sets allow accumulation of such sparse parts. The key comparison lies in the fact that every nowhere dense set is of first category, but first category sets might not be nowhere dense themselves, showing a broader classification in terms of topological size and density.
Differences Between Open and Closed Sets
Open sets in topology are defined by containing none of their boundary points, allowing each point to have a neighborhood fully contained within the set, while closed sets include all their boundary points, making them comprehensive in limit points. The distinction between first category (meager) and second category sets lies in their topological size, where first category sets are countable unions of nowhere dense sets, contrasted with second category sets which are not meager, often being "large" or dense in some sense. Nowhere dense sets have closures with empty interiors, emphasizing their sparse distribution, which contrasts with the robustness of second category or closed sets that maintain substantial presence through boundary inclusion or dense interiors.
Implications of Category in Analysis
First category sets, also known as meager sets, consist of countable unions of nowhere dense sets and are crucial in functional analysis for understanding generic properties of function spaces. Second category sets, which are not of the first category, represent "large" or prevalent subsets in complete metric spaces, influencing the Baire Category Theorem and its implications on continuity and density of functions. The distinction between open, closed, and nowhere dense sets underpins these categories, with nowhere dense sets having empty interiors and being sparse, while closed sets may be large and structurally significant, affecting convergence and stability in analysis.
Conclusion: Applications of Set Categories
Set categories such as first category (meager sets) and second category sets are crucial in functional analysis and topology, distinguishing between negligible and substantial subsets of spaces. Open sets and closed sets define topological boundaries essential for continuity, convergence, and compactness properties, while nowhere dense sets characterize sparse subsets with empty interior. Applications leverage these distinctions in solving differential equations, optimizing algorithms, and analyzing Baire spaces, where categorizing sets guides measure theory and real analysis frameworks.
First category, Second category, Open set, Closed set, Nowhere dense set Infographic
 libterm.com
libterm.com