An adjoint functor is a fundamental concept in category theory, describing a pair of functors that stand in a specific correspondence between categories, often simplifying complex mathematical structures. These functors come in left and right pairs, where the left adjoint functor preserves colimits and the right adjoint preserves limits, enabling efficient translations between different categorical contexts. Dive deeper into the article to explore how adjoint functors impact various branches of mathematics and their practical applications.
Table of Comparison
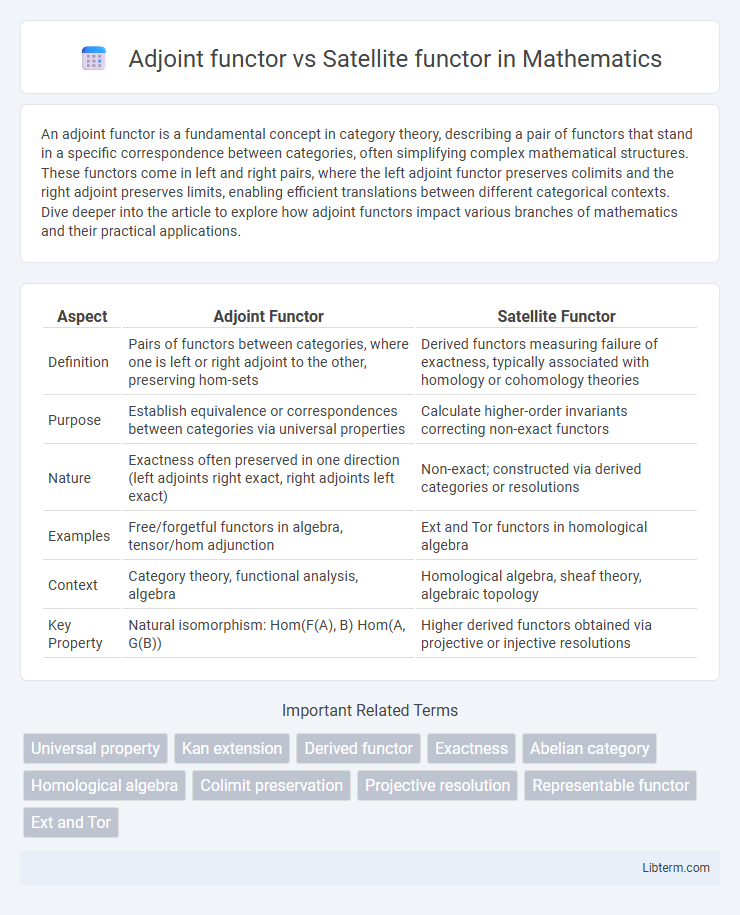
| Aspect | Adjoint Functor | Satellite Functor |
|---|---|---|
| Definition | Pairs of functors between categories, where one is left or right adjoint to the other, preserving hom-sets | Derived functors measuring failure of exactness, typically associated with homology or cohomology theories |
| Purpose | Establish equivalence or correspondences between categories via universal properties | Calculate higher-order invariants correcting non-exact functors |
| Nature | Exactness often preserved in one direction (left adjoints right exact, right adjoints left exact) | Non-exact; constructed via derived categories or resolutions |
| Examples | Free/forgetful functors in algebra, tensor/hom adjunction | Ext and Tor functors in homological algebra |
| Context | Category theory, functional analysis, algebra | Homological algebra, sheaf theory, algebraic topology |
| Key Property | Natural isomorphism: Hom(F(A), B) Hom(A, G(B)) | Higher derived functors obtained via projective or injective resolutions |
Introduction to Functors in Category Theory
Adjoint functors establish a fundamental relationship between two categories by pairing a left and right functor that satisfy a specific hom-set isomorphism, enabling the transfer of structure and properties. Satellite functors arise in homological algebra as derived functors, capturing higher-level information about objects by measuring the failure of exactness in sequences. Understanding these functors in category theory provides insight into the interplay between structures, where adjoint functors offer universal constructions and satellite functors extend homological techniques.
Defining Adjoint Functors
Adjoint functors consist of a pair of functors between two categories that establish a natural isomorphism between hom-sets, providing a formal framework for universal constructions in category theory. Defining an adjoint functor involves identifying a left adjoint functor \( F: \mathcal{C} \to \mathcal{D} \) and a right adjoint functor \( G: \mathcal{D} \to \mathcal{C} \) such that for each object \( c \) in category \( \mathcal{C} \) and \( d \) in category \(\mathcal{D}\), there is a natural bijection \( \mathrm{Hom}_{\mathcal{D}}(F(c), d) \cong \mathrm{Hom}_{\mathcal{C}}(c, G(d)) \). Satellite functors, by contrast, arise in homological algebra as derived-like functors measuring the failure of exactness in functor applications, rather than establishing universal properties.
Understanding Satellite Functors
Satellite functors extend homological algebra by associating derived functors to a given functor, capturing higher-dimensional information beyond immediate images. Unlike adjoint functors, which express a direct correspondence between categories and preserve hom-sets, satellite functors analyze how a functor behaves with respect to exact sequences, often computed via projective or injective resolutions. Understanding satellite functors requires grasping their role in measuring the failure of exactness and their pivotal use in cohomology theories and derived categories.
Key Differences Between Adjoint and Satellite Functors
Adjoint functors form pairs of functors between categories, characterized by a natural isomorphism between hom-sets that reflects a universal mapping property, often used to describe constructions like free and forgetful functors. Satellite functors arise in homological algebra as derived functors, measuring the failure of exactness of a given functor and often used to compute Ext and Tor groups. The key difference lies in their roles: adjoint functors establish fundamental correspondences between categories, while satellite functors capture homological information related to exactness and cohomology theories.
Universal Properties: A Comparative Analysis
Adjoint functors are characterized by a pair of functors between categories that establish a natural isomorphism between hom-sets, encapsulating a universal property that defines one functor as the best approximation to the inverse of the other. Satellite functors, often derived from homological algebra, extend a given functor to measure its failure to be exact, relying on universal properties linked to derived functors to capture higher-dimensional homological information. The universal property of adjoint functors provides a direct and intrinsic characterization of morphisms, while satellite functors encode universal properties of exactness and extension, highlighting a complementary yet distinct role in categorical and homological contexts.
Construction Methods of Adjoint vs Satellite Functors
Adjoint functors are constructed through universal properties involving hom-set isomorphisms that establish a natural bijection between morphisms, often realized via initial or terminal objects in comma categories. Satellite functors arise from derived functor techniques, typically using resolutions and exact sequences in abelian categories to extract homological information beyond exactness. The construction of adjoint functors emphasizes categorical universality, while satellite functors rely on homological algebra tools like projective, injective, or flat resolutions to define right or left satellites.
Applications of Adjoint Functors in Mathematics
Adjoint functors play a crucial role in category theory by establishing a correspondence between different mathematical structures, facilitating the transfer of properties and results across fields such as algebra, topology, and logic. Their applications include constructing free objects, providing solutions to universal mapping problems, and enabling the formulation of derived functors in homological algebra. These features make adjoint functors indispensable tools in modern mathematical research and problem solving.
Use Cases of Satellite Functors in Homological Algebra
Satellite functors extend the concept of derived functors by providing a systematic approach to measure the failure of exactness beyond the first degree, crucial for analyzing long exact sequences in homological algebra. They are particularly useful in calculating Ext and Tor groups, enabling deeper exploration of module extensions and tensor product behaviors. These functors also facilitate the study of sheaf cohomology and spectral sequences, making them indispensable tools in algebraic topology and algebraic geometry.
Limitations and Strengths: Adjoint and Satellite Functors
Adjoint functors excel at establishing precise correspondences between categories, providing a robust framework to transfer structures and preserve limits or colimits, but their reliance on the existence of universal morphisms can limit applicability in complex or large categories. Satellite functors extend the concept of derived functors beyond abelian categories, allowing homological constructions in more general settings, yet they often require intricate exactness conditions and may lack the elegance and generality of adjoint pairs. The strengths of adjoint functors lie in their unifying categorical properties and wide use in algebra and topology, while satellite functors offer flexibility in homological algebra at the cost of increased technical complexity.
Conclusion: Choosing Between Adjoint and Satellite Functors
Choosing between adjoint functors and satellite functors depends on the context of their application within category theory and homological algebra. Adjoint functors provide a powerful framework for establishing equivalences and universal properties, often simplifying complex constructions through their inherent naturality and bijection of hom-sets. Satellite functors, by contrast, excel in deriving and approximating cohomological information, making them indispensable in contexts requiring exact sequences and higher derived functors.
Adjoint functor Infographic
 libterm.com
libterm.com