Cohomology groups provide crucial algebraic invariants that capture topological and geometric properties of mathematical spaces. They play a central role in fields such as algebraic topology, differential geometry, and complex analysis by enabling the classification and study of structures through their cohomological characteristics. Discover how cohomology groups can deepen your understanding of advanced mathematical concepts in the full article.
Table of Comparison
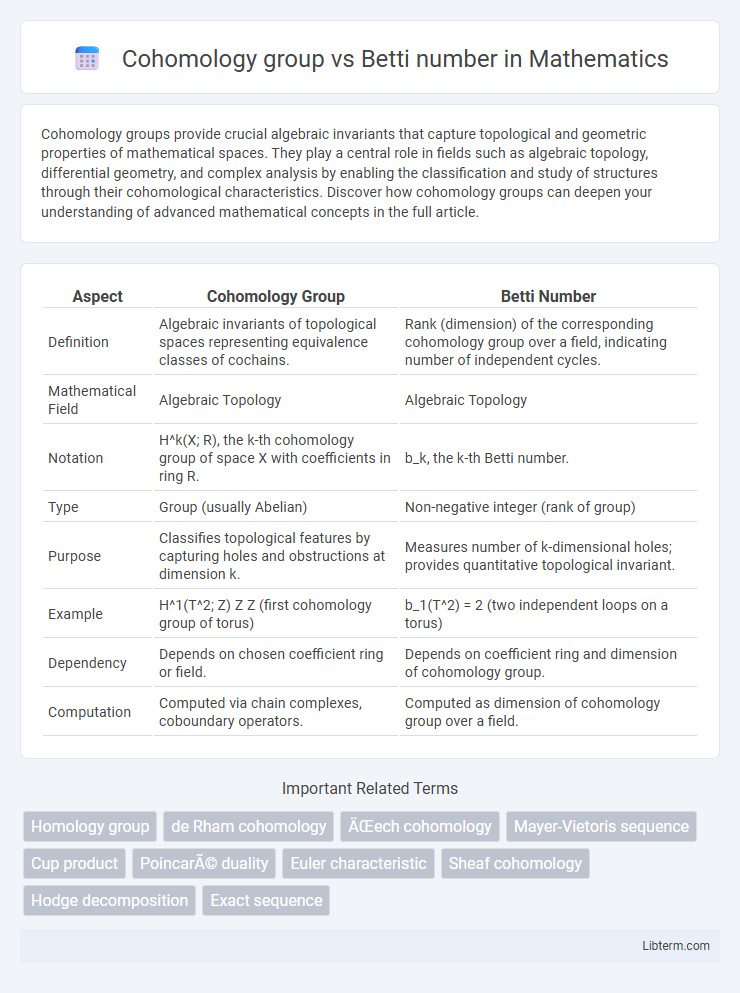
| Aspect | Cohomology Group | Betti Number |
|---|---|---|
| Definition | Algebraic invariants of topological spaces representing equivalence classes of cochains. | Rank (dimension) of the corresponding cohomology group over a field, indicating number of independent cycles. |
| Mathematical Field | Algebraic Topology | Algebraic Topology |
| Notation | H^k(X; R), the k-th cohomology group of space X with coefficients in ring R. | b_k, the k-th Betti number. |
| Type | Group (usually Abelian) | Non-negative integer (rank of group) |
| Purpose | Classifies topological features by capturing holes and obstructions at dimension k. | Measures number of k-dimensional holes; provides quantitative topological invariant. |
| Example | H^1(T^2; Z) Z Z (first cohomology group of torus) | b_1(T^2) = 2 (two independent loops on a torus) |
| Dependency | Depends on chosen coefficient ring or field. | Depends on coefficient ring and dimension of cohomology group. |
| Computation | Computed via chain complexes, coboundary operators. | Computed as dimension of cohomology group over a field. |
Introduction to Cohomology Groups
Cohomology groups are algebraic structures that provide a powerful tool for classifying topological spaces by capturing global properties through functions defined on chains of a space. These groups serve as duals to homology groups and are essential in distinguishing spaces that have the same homology but different cohomological features. Betti numbers arise as ranks of homology groups, representing the number of independent cycles, while cohomology groups offer richer algebraic invariants that include information about torsion and cup products.
Understanding Betti Numbers
Betti numbers quantify the rank of cohomology groups, providing essential topological invariants that measure the number of independent cycles in each dimension of a space. These numbers reflect the dimensions of vector spaces formed by cohomology groups over a field, capturing holes or voids in various dimensions. Understanding Betti numbers is key to analyzing the shape and connectivity of topological spaces through algebraic topology.
Historical Background and Development
Cohomology groups were introduced in the 20th century as algebraic tools to classify topological spaces by capturing global properties through algebraic invariants. The concept of Betti numbers, named after Enrico Betti, originated in the 19th century and provided numerical measures of the connectivity of spaces, counting independent cycles in each dimension. The development of cohomology theory extended Betti's numerical invariants by associating groups to spaces, enabling richer algebraic structures and deeper insights into topological and geometric phenomena.
Mathematical Definitions and Notation
The cohomology group \( H^n(X; R) \) is an algebraic invariant of a topological space \( X \), defined as the quotient of the kernel of the coboundary operator by its image, capturing \( n \)-dimensional cohomological features with coefficients in a ring \( R \). The Betti number \( b_n \) is the rank of the \( n \)-th homology group \( H_n(X; \mathbb{Z}) \), which equals the dimension of the \( n \)-th cohomology group \( H^n(X; \mathbb{Q}) \) as a vector space over the rationals, quantifying the number of \( n \)-dimensional holes. The notation emphasizes the dual nature of homology and cohomology, where \( b_n = \dim H^n(X; \mathbb{Q}) = \dim H_n(X; \mathbb{Q}) \), linking topological features to algebraic structures.
Key Differences Between Cohomology Groups and Betti Numbers
Cohomology groups are algebraic structures that classify topological spaces by measuring the number and types of holes using chain complexes and cochains, while Betti numbers are numerical invariants representing the rank of these groups, indicating the count of independent cycles in each dimension. The key difference lies in cohomology groups containing detailed algebraic information, such as torsion and cup product structure, whereas Betti numbers provide a simplified summary as non-negative integers. Cohomology groups enable richer topological analysis through their module and ring structures, whereas Betti numbers serve primarily as a quantitative snapshot of topological complexity.
Interrelation: From Cohomology Groups to Betti Numbers
Cohomology groups provide algebraic structures that capture topological features of a space, with each group corresponding to a specific degree or dimension. Betti numbers arise as the ranks of these cohomology groups, quantifying the number of independent cycles in each dimension. The transition from cohomology groups to Betti numbers enables the classification of spaces through numerical invariants reflecting their topology.
Computational Aspects and Algorithms
Cohomology groups provide algebraic structures that capture topological features of spaces, and their computation often relies on algorithms involving chain complexes and boundary operators represented as matrices. Betti numbers, as ranks of these cohomology groups, offer numerical invariants measuring independent cycles, computable via matrix rank calculations or persistent homology algorithms in computational topology. Efficient algorithms for computing Betti numbers leverage sparse matrix reductions and data structures like boundary and coboundary matrices, optimizing complexity in applications such as topological data analysis and mesh processing.
Applications in Topology and Geometry
Cohomology groups provide algebraic invariants that classify topological spaces by capturing global geometric structures, essential for distinguishing complex manifolds and fiber bundles. Betti numbers, defined as the ranks of these cohomology groups, quantify independent cycles and holes, serving as critical numerical topological invariants for analyzing shapes and connectivity. Applications in topology and geometry leverage cohomology theories and Betti numbers to study manifold properties, facilitate classification of spaces, and solve problems in areas such as Morse theory, Poincare duality, and algebraic geometry.
Cohomology and Betti Numbers in Data Analysis
Cohomology groups provide algebraic structures that measure the shape and connectivity of data spaces, capturing essential topological features for data analysis. Betti numbers, derived from the ranks of these cohomology groups, quantify the number of independent components, holes, and voids in various dimensions, enabling the characterization of complex data patterns. Together, cohomology groups and Betti numbers support persistent homology techniques, offering robust tools for extracting multiscale topological information from high-dimensional datasets.
Conclusion and Future Perspectives
Cohomology groups provide a rich algebraic structure that captures topological invariants of spaces, offering finer distinctions than Betti numbers, which count the rank of these groups and summarize the number of independent cycles. Future research aims to deepen the interplay between cohomology and modern fields such as persistent homology, emphasizing computational methods to handle complex data and applications in higher-dimensional topology. Developing advanced algorithms for effective cohomology computation will enhance both theoretical insights and practical applications in data analysis and geometric modeling.
Cohomology group Infographic
 libterm.com
libterm.com