Fusion categories are pivotal in modern mathematics and theoretical physics, serving as algebraic structures that encapsulate symmetries and particle interactions in topological quantum field theories. These categories consist of simple objects and morphisms that fuse according to specific rules, providing a framework for understanding quantum symmetries and invariants in low-dimensional topology. Discover how fusion categories shape advanced research and applications by exploring the rest of the article.
Table of Comparison
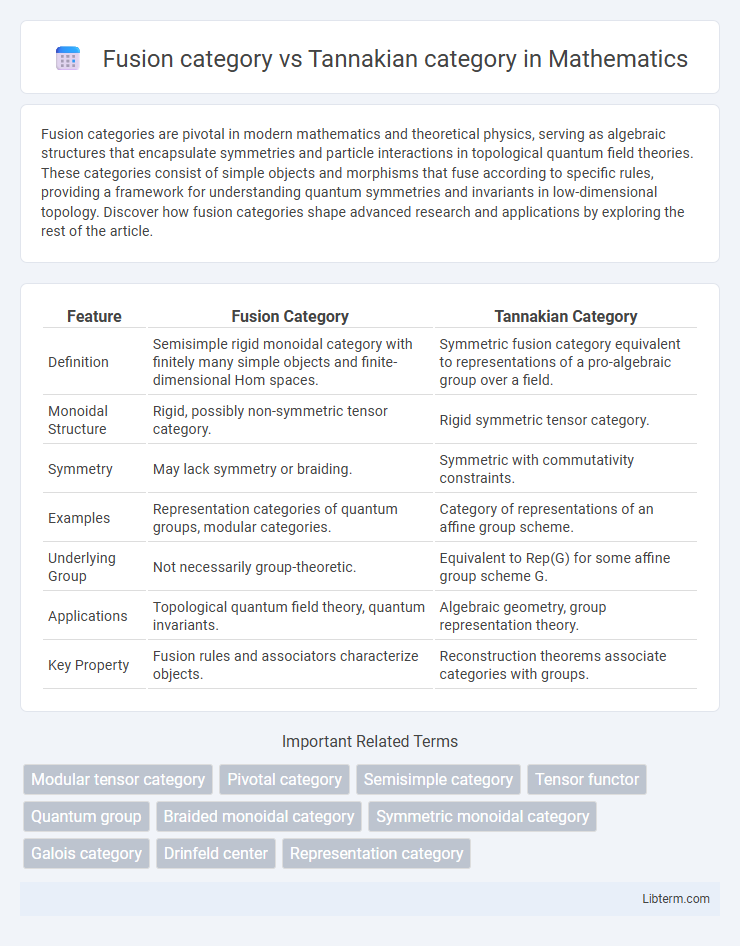
| Feature | Fusion Category | Tannakian Category |
|---|---|---|
| Definition | Semisimple rigid monoidal category with finitely many simple objects and finite-dimensional Hom spaces. | Symmetric fusion category equivalent to representations of a pro-algebraic group over a field. |
| Monoidal Structure | Rigid, possibly non-symmetric tensor category. | Rigid symmetric tensor category. |
| Symmetry | May lack symmetry or braiding. | Symmetric with commutativity constraints. |
| Examples | Representation categories of quantum groups, modular categories. | Category of representations of an affine group scheme. |
| Underlying Group | Not necessarily group-theoretic. | Equivalent to Rep(G) for some affine group scheme G. |
| Applications | Topological quantum field theory, quantum invariants. | Algebraic geometry, group representation theory. |
| Key Property | Fusion rules and associators characterize objects. | Reconstruction theorems associate categories with groups. |
Introduction to Fusion Categories and Tannakian Categories
Fusion categories are rigid, semisimple tensor categories with finitely many simple objects and finite-dimensional Hom spaces, playing a crucial role in quantum algebra and topological quantum field theory. Tannakian categories are a special class of fusion categories equivalent to the representation categories of affine group schemes, characterized by a fiber functor to vector spaces that preserves tensor structure. Understanding the structural differences between fusion categories and Tannakian categories provides key insights into their applications in representation theory and categorical duality.
Defining Fusion Categories: Core Concepts
Fusion categories are rigid, semisimple tensor categories with finitely many isomorphism classes of simple objects, finite-dimensional Hom spaces, and simple unit objects, often arising in quantum algebra and topological quantum field theory. Tannakian categories form a special type of fusion category equivalent to the representation category of an affine group scheme, characterized by a fiber functor to vector spaces preserving the tensor structure. The core concept distinguishing fusion categories lies in their fusion rules and categorical dimensions, while Tannakian categories are uniquely defined by their symmetric braiding and fiber functor that enables reconstruction of the underlying group.
Understanding Tannakian Categories: Key Features
Tannakian categories are rigid, abelian tensor categories equipped with a fiber functor to vector spaces, allowing reconstruction of affine group schemes via Tannaka duality. They possess symmetric braidings and dual objects, enabling a powerful link between category theory and algebraic group theory. Fusion categories, in contrast, are semisimple, rigid tensor categories with finitely many simple objects and non-symmetric braidings, often used to study topological quantum field theories.
Historical Context and Development
Fusion categories originated in the study of operator algebras and low-dimensional quantum topology during the late 20th century, serving as algebraic frameworks for topological quantum field theories. Tannakian categories, rooted in the work of Tannaka and Krein from the mid-20th century, provide a categorical approach to group representation theory by reconstructing groups from symmetric monoidal categories. The development of fusion categories further extended the Tannakian duality concept by relaxing symmetry constraints, enabling applications in modular tensor categories and quantum groups.
Fundamental Differences in Structure
Fusion categories are semisimple, rigid, monoidal categories with finitely many simple objects and finite-dimensional Hom spaces, characterized by a complex fusion rule algebra. Tannakian categories are symmetric fusion categories, equivalent to the category of representations of a pro-algebraic group, reflecting an underlying group symmetry in their structure. The fundamental difference lies in the presence of a symmetric braiding in Tannakian categories, whereas fusion categories may have non-symmetric braidings or none, leading to richer topological and algebraic structures.
Examples of Fusion vs. Tannakian Categories
Fusion categories include examples such as the representation categories of quantum groups at roots of unity and the Fibonacci category derived from the Temperley-Lieb algebra, characterized by nontrivial associators and fusion rules. Tannakian categories arise primarily as the representation categories of affine group schemes, including classical examples like Rep(G) for a finite group G or Rep(GL_n) over a field, featuring a fiber functor to vector spaces. These examples reflect the key distinction: fusion categories generalize group representation categories with more complex fusion, while Tannakian categories are equivalent to symmetric tensor categories realized by group representations.
Applications in Mathematics and Physics
Fusion categories provide a framework for studying topological quantum field theories by categorizing particle-like excitations with nontrivial braiding, playing a central role in low-dimensional topology and quantum computing. Tannakian categories, characterized by their connection to linear representations of group schemes, are crucial in understanding symmetry and group actions in algebraic geometry and number theory. Both categories facilitate the exploration of symmetry and duality, with fusion categories linking to anyon models in physics and Tannakian categories underpinning the theory of motives and Galois groups in mathematics.
Categorical Tensor Structures Compared
Fusion categories are semisimple rigid tensor categories with finitely many simple objects and finite-dimensional Hom spaces, exhibiting pivotal structures that enable duality and fusion rules similar to those in representation theory of quantum groups. Tannakian categories, typically symmetric rigid abelian tensor categories over a field with a fiber functor, serve as categorical analogs of affine group schemes, ensuring equivalences to representation categories of pro-algebraic groups. The categorical tensor structures in fusion categories emphasize non-symmetric braidings and modular data, while Tannakian categories inherently possess symmetric tensor structures facilitating symmetric monoidal equivalences essential for reconstruction theorems in Tannaka duality.
Symmetry, Duality, and Group Actions
Fusion categories exhibit rich symmetry structures characterized by semisimple, rigid tensor categories with finitely many simple objects, facilitating duality through pivotal objects and categorical dimensions. Tannakian categories arise as neutral Tannakian categories equivalent to the representation categories of affine group schemes, hosting canonical fiber functors that encode group actions and allow reconstruction of the affine group via Tannaka-Krein duality. The interplay between duality and symmetry in fusion categories generalizes the classical group symmetries found in Tannakian categories, connecting categorical duals with group-theoretic dualities and actions through braided and modular structures.
Open Problems and Future Directions
The study of fusion categories and Tannakian categories involves open problems such as classification challenges, understanding modularity, and exploring connections with quantum groups and topological quantum field theories. Future directions prioritize developing invariants for fusion categories, analyzing their representation theory, and extending the framework of categorification to broader algebraic structures. Investigating the role of Tannakian duality in non-semisimple settings and its implications for higher categories remains a pivotal research frontier.
Fusion category Infographic
 libterm.com
libterm.com