A separating hyperplane is a fundamental concept in machine learning used to divide data points into distinct classes by finding the optimal linear boundary. This technique is essential for algorithms like Support Vector Machines, where it maximizes the margin between different categories to improve classification accuracy. Explore the full article to understand how a separating hyperplane can enhance your data analysis and model performance.
Table of Comparison
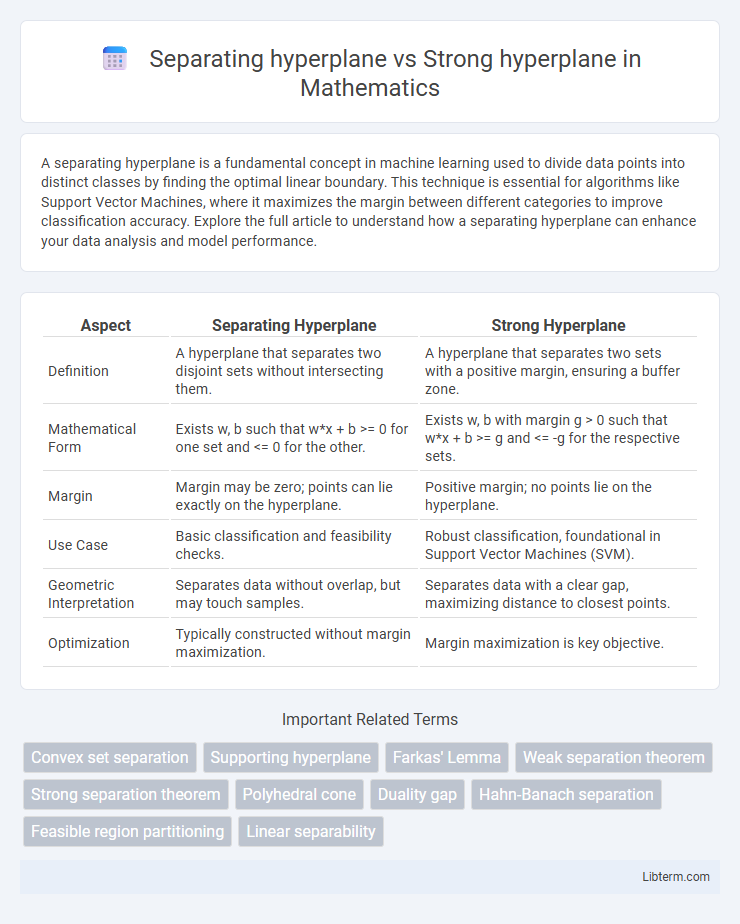
| Aspect | Separating Hyperplane | Strong Hyperplane |
|---|---|---|
| Definition | A hyperplane that separates two disjoint sets without intersecting them. | A hyperplane that separates two sets with a positive margin, ensuring a buffer zone. |
| Mathematical Form | Exists w, b such that w*x + b >= 0 for one set and <= 0 for the other. | Exists w, b with margin g > 0 such that w*x + b >= g and <= -g for the respective sets. |
| Margin | Margin may be zero; points can lie exactly on the hyperplane. | Positive margin; no points lie on the hyperplane. |
| Use Case | Basic classification and feasibility checks. | Robust classification, foundational in Support Vector Machines (SVM). |
| Geometric Interpretation | Separates data without overlap, but may touch samples. | Separates data with a clear gap, maximizing distance to closest points. |
| Optimization | Typically constructed without margin maximization. | Margin maximization is key objective. |
Introduction to Hyperplanes in Machine Learning
Hyperplanes in machine learning serve as decision boundaries that classify data points by separating different classes in a feature space. A separating hyperplane distinctly divides data into two categories without overlap, enabling linear classification in algorithms such as Support Vector Machines (SVM). Strong hyperplanes, often related to maximizing the margin between classes, enhance model robustness by ensuring optimal separation and reducing classification errors.
Defining the Concept of a Separating Hyperplane
A separating hyperplane is a linear decision boundary that divides data points from two classes without any overlap, ensuring all points from each class lie on opposite sides of the hyperplane. In contrast, a strong hyperplane not only separates classes but also maximizes the margin, the distance between the hyperplane and the nearest data points, enhancing classification robustness. Defining the separating hyperplane involves finding a vector \( \mathbf{w} \) and bias \( b \) such that for all training samples \( x_i \), the condition \( y_i (\mathbf{w} \cdot x_i + b) > 0 \) holds true, where \( y_i \) are class labels.
Understanding Strong Hyperplanes
Strong hyperplanes represent a subset of separating hyperplanes characterized by maximizing the margin between distinct classes in a dataset, ensuring a robust classification boundary. Unlike general separating hyperplanes, which simply divide classes, strong hyperplanes optimize the distance to the nearest data points from each class, enhancing model generalization. This principle underlies Support Vector Machines (SVMs), where the strong hyperplane is identified to achieve the best trade-off between classification accuracy and margin size.
Geometric Interpretation: Separating vs Strong Hyperplanes
A separating hyperplane divides data points of different classes by a clear boundary with possible data points lying on the margin, ensuring no overlap but not necessarily maximizing the margin. A strong hyperplane, characterized by its maximum margin, geometrically maximizes the distance between itself and the closest data points from each class, providing better generalization in classification tasks. The geometric interpretation emphasizes how strong hyperplanes enforce stricter separation criteria, improving robustness compared to general separating hyperplanes.
Mathematical Formulations and Differences
A separating hyperplane in a d-dimensional space is defined by the equation \( \mathbf{w} \cdot \mathbf{x} + b = 0 \), where it classifies data points by ensuring \( y_i (\mathbf{w} \cdot \mathbf{x}_i + b) > 0 \) for all samples \( (\mathbf{x}_i, y_i) \), effectively distinguishing classes without necessarily maximizing margin. A strong hyperplane, commonly referred to as a maximum-margin or optimal separating hyperplane in support vector machines (SVM), not only satisfies the separating condition but also maximizes the margin \( \frac{2}{\|\mathbf{w}\|} \), solving the optimization problem \( \min_{\mathbf{w}, b} \frac{1}{2} \|\mathbf{w}\|^2 \) subject to \( y_i (\mathbf{w} \cdot \mathbf{x}_i + b) \geq 1 \). The key difference lies in margin maximization: a separating hyperplane merely separates classes, whereas a strong hyperplane optimizes margin width, improving generalization and robustness in classification tasks.
Role of Hyperplanes in Classification Algorithms
Hyperplanes serve as decision boundaries in classification algorithms, separating data points of different classes within the feature space. A separating hyperplane distinctly divides classes without overlap, ensuring perfect classification in linearly separable data. Strong hyperplanes maximize the margin, enhancing robustness and generalization in support vector machines by selecting the optimal hyperplane that separates classes with the widest possible gap.
Margin Analysis: Soft vs Hard Margin
A separating hyperplane divides data points into distinct classes without overlap, corresponding to a hard margin in Support Vector Machines (SVMs) where no misclassifications occur and the margin is maximized to achieve perfect separation. A strong hyperplane extends this concept by allowing a soft margin, tolerating some misclassifications to handle noisy or non-linearly separable data, optimizing both the margin width and classification errors through a regularization parameter. Margin analysis contrasts hard margin SVM's strict boundary enforcement with soft margin SVM's balance between maximizing margin and minimizing classification error, critical for practical applications with overlapping data distributions.
Practical Implications in Support Vector Machines
Separating hyperplanes in Support Vector Machines (SVMs) define the decision boundary that divides classes, but strong hyperplanes maximize the margin between classes, enhancing generalization and robustness. Practical implications include improved classification accuracy and resilience to overfitting when using strong hyperplanes, as they create wider margins that reduce classification errors on unseen data. Implementing strong hyperplanes through margin maximization techniques directly impacts model performance, making them crucial for effective SVM training and deployment.
Examples and Visualizations
Separating hyperplanes divide data points into distinct classes without overlap, commonly illustrated by linear classifiers like Support Vector Machines (SVM) separating two linearly separable classes. Strong hyperplanes often refer to maximum-margin hyperplanes in SVMs, which maximize the distance between the closest points of different classes, enhancing generalization. Visualizations typically show the separating hyperplane as a line or plane between clusters, while the strong hyperplane appears equidistant from support vectors, emphasizing margin maximization.
Conclusion: Choosing the Right Hyperplane
Selecting the right hyperplane hinges on the problem's margin requirements and data distribution; a separating hyperplane is suitable for perfectly linearly separable data, ensuring zero classification error. Strong hyperplanes maximize the margin between classes, enhancing generalization and robustness to noise, making them ideal for real-world, imperfect datasets. Prioritizing strong hyperplanes in support vector machines (SVMs) typically yields better predictive performance and stability.
Separating hyperplane Infographic
 libterm.com
libterm.com