The Whitehead product is a fundamental operation in algebraic topology that combines two homotopy classes of maps to produce a new class, reflecting the non-commutative structure of homotopy groups. This product captures essential information about the interaction between loops and spheres within a topological space, revealing deeper insights into its homotopy type. Explore the rest of this article to understand how the Whitehead product influences the study of topological spaces and their homotopy groups.
Table of Comparison
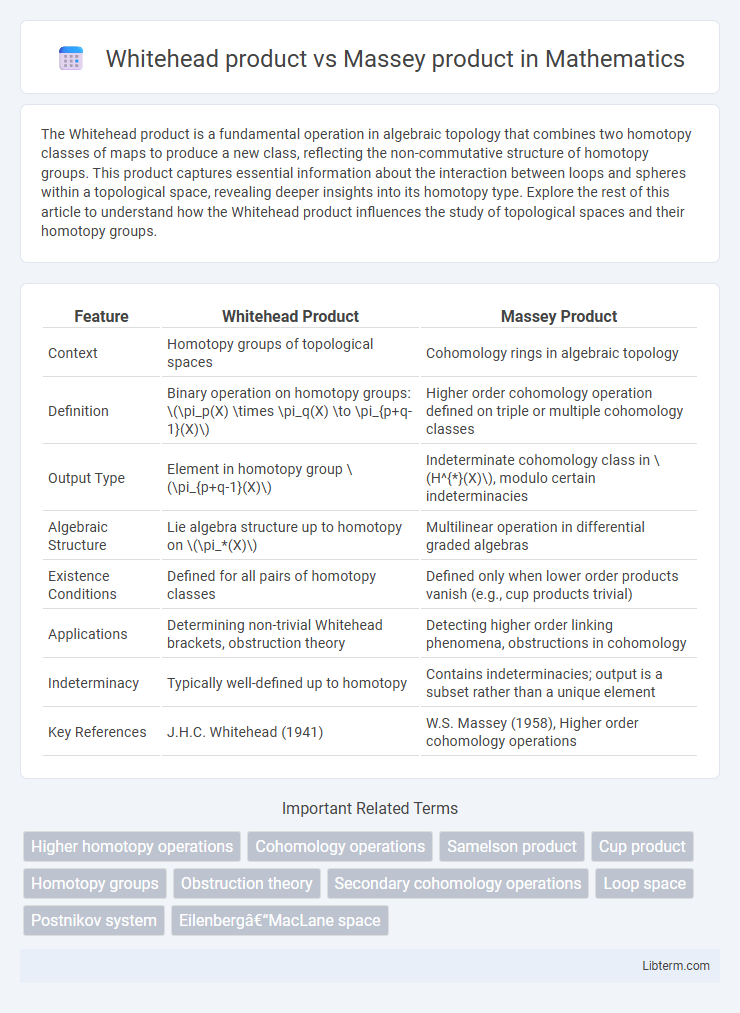
| Feature | Whitehead Product | Massey Product |
|---|---|---|
| Context | Homotopy groups of topological spaces | Cohomology rings in algebraic topology |
| Definition | Binary operation on homotopy groups: \(\pi_p(X) \times \pi_q(X) \to \pi_{p+q-1}(X)\) | Higher order cohomology operation defined on triple or multiple cohomology classes |
| Output Type | Element in homotopy group \(\pi_{p+q-1}(X)\) | Indeterminate cohomology class in \(H^{*}(X)\), modulo certain indeterminacies |
| Algebraic Structure | Lie algebra structure up to homotopy on \(\pi_*(X)\) | Multilinear operation in differential graded algebras |
| Existence Conditions | Defined for all pairs of homotopy classes | Defined only when lower order products vanish (e.g., cup products trivial) |
| Applications | Determining non-trivial Whitehead brackets, obstruction theory | Detecting higher order linking phenomena, obstructions in cohomology |
| Indeterminacy | Typically well-defined up to homotopy | Contains indeterminacies; output is a subset rather than a unique element |
| Key References | J.H.C. Whitehead (1941) | W.S. Massey (1958), Higher order cohomology operations |
Introduction to Algebraic Topology Products
Whitehead product and Massey product are fundamental operations in algebraic topology used to study the homotopy groups of topological spaces. Whitehead product combines elements of homotopy groups to detect nontrivial higher homotopy interactions, while Massey product extends cup product in cohomology to capture higher-order linking phenomena beyond primary operations. Both products serve as crucial tools in distinguishing complex topological structures and revealing hidden algebraic relations within spaces.
Defining the Whitehead Product
The Whitehead product is a bilinear operation defined on the homotopy groups of a pointed topological space, mapping two homotopy classes in \(\pi_p(X)\) and \(\pi_q(X)\) to a class in \(\pi_{p+q-1}(X)\). It arises from loop space constructions and captures nontrivial interactions between homotopy groups, often encoding primary homotopy invariants. Unlike the Massey product, which is a higher-order cohomology operation detecting more subtle linking phenomena, the Whitehead product operates directly on homotopy groups via the commutator bracket on loop spaces.
Defining the Massey Product
The Massey product is a higher-order cohomology operation generalizing the cup product by capturing information about the nontrivial interactions of three or more cohomology classes in differential graded algebras. Unlike the Whitehead product, which arises in homotopy groups and measures the failure of maps to commute up to homotopy, the Massey product is defined using representatives of cohomology classes and their indeterminacies within a specific cochain complex. This construction provides insights into the structure of the cohomology ring beyond primary products, detecting hidden extensions and higher-order relations in algebraic topology.
Historical Context and Development
The Whitehead product, introduced by J.H.C. Whitehead in the 1940s, emerged from early work in homotopy theory to describe the interaction of homotopy groups via a bilinear operation. The Massey product, developed in the 1950s by William Massey, extended classical cup products in cohomology to higher-order operations, revealing intricate algebraic structures in differential graded algebras and topological spaces. Both products have played pivotal roles in algebraic topology, with the Whitehead product influencing the understanding of homotopy groups, while the Massey product advanced the study of secondary cohomology operations and obstructions.
Algebraic Structures Underlying Each Product
The Whitehead product is rooted in homotopy theory, representing a bilinear operation in the homotopy groups of a topological space, closely related to the Lie algebra structure induced by the Samelson product. The Massey product arises in the cohomology ring as a higher-order cohomological operation capturing nontrivial extensions beyond cup products, reflecting intricate associativity relations encoded in differential graded algebras. Whitehead products emphasize homotopical algebra and looping structures, while Massey products depend on the existence of specific defining systems within differential graded associative algebras and reveal deeper algebraic complexities in cohomology.
Computational Methods for Whitehead and Massey Products
Computational methods for Whitehead products involve the use of homotopy spectral sequences and algorithmic approaches in homotopy theory to determine higher-order compositions in loop spaces. Massey products computation relies on cohomological algebra techniques, specifically manipulating differential graded algebras and spectral sequences to detect nontrivial higher cohomology operations. Advances in computational topology software have enabled explicit calculations of both Whitehead and Massey products, facilitating deeper understanding of their roles in homotopy theory and algebraic topology.
Applications in Homotopy and Cohomology Theory
Whitehead products capture nontrivial interactions in the homotopy groups of spheres, revealing higher-order linking phenomena crucial for distinguishing homotopy types. Massey products extend this concept in cohomology, encoding secondary cohomological operations that detect obstructions to formality and provide finer algebraic invariants in differential graded algebras. Both tools facilitate the study of space structure, with Whitehead products focusing on homotopy group interactions and Massey products uncovering hidden product structures in cohomology rings.
Key Differences Between Whitehead and Massey Products
Whitehead products arise in homotopy theory, combining elements of homotopy groups to reflect non-abelian structures of topological spaces, while Massey products are higher-order cohomology operations detecting complex algebraic relations in cohomology rings. The Whitehead product is bilinear and defined on the homotopy groups of a space, producing new elements of lower-dimensional homotopy groups, whereas Massey products involve triple or higher multiple cohomology classes, revealing hidden extensions in the cohomology algebra. Whitehead products primarily measure interactions in homotopy groups, whereas Massey products provide obstructions to formality and can detect non-trivial linking in higher cohomology.
Illustrative Examples and Calculations
The Whitehead product, an operation in homotopy groups, measures the non-commutativity of loop space structures, exemplified by the Whitehead product in \(\pi_*(S^n)\) where \([i_n, i_n] \neq 0\) for the identity map \(i_n\) of the \(n\)-sphere. Massey products, higher-order cohomology operations, reveal hidden extensions between cohomology classes, illustrated by the triple Massey product \(\langle \alpha, \beta, \gamma \rangle\) in the cohomology of a wedge of spheres, which can detect nontrivial linking phenomena undetected by cup products. Calculations of Whitehead products often use the Samelson product in loop spaces, while Massey product computations rely on choosing cochain representatives to verify indeterminacies and nontriviality in differential graded algebras.
Open Problems and Future Directions
Whitehead product and Massey product remain pivotal in homotopy theory, with open problems centered on understanding their higher-order interactions and potential generalizations. Future research aims to elucidate the precise algebraic structures governing Massey products in non-simply connected spaces and the role of Whitehead products in unstable homotopy groups. Advances in computational methods and homotopical algebra may unlock new classifications and applications in topological data analysis and algebraic geometry.
Whitehead product Infographic
 libterm.com
libterm.com