Uniform convergence ensures that a sequence of functions converges to a limit function consistently across the entire domain, maintaining a fixed degree of closeness. This concept is crucial in mathematical analysis, especially when dealing with function series, as it guarantees the preservation of continuity, integrability, and differentiability in the limit function. Explore the rest of the article to deepen your understanding of uniform convergence and its implications in real-world applications.
Table of Comparison
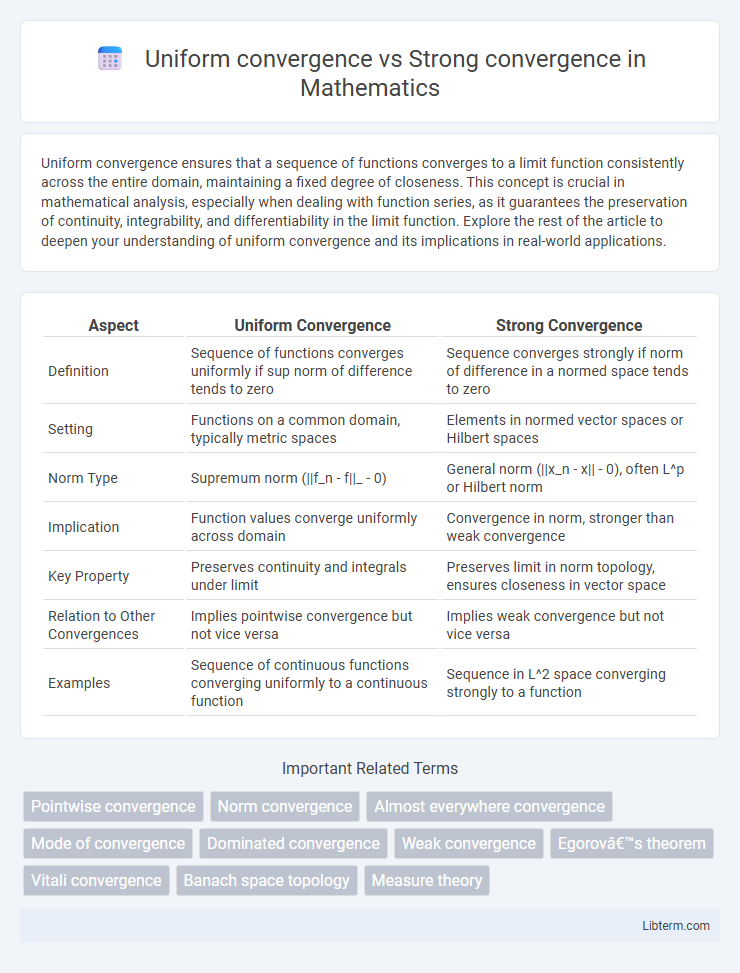
| Aspect | Uniform Convergence | Strong Convergence |
|---|---|---|
| Definition | Sequence of functions converges uniformly if sup norm of difference tends to zero | Sequence converges strongly if norm of difference in a normed space tends to zero |
| Setting | Functions on a common domain, typically metric spaces | Elements in normed vector spaces or Hilbert spaces |
| Norm Type | Supremum norm (||f_n - f||_ - 0) | General norm (||x_n - x|| - 0), often L^p or Hilbert norm |
| Implication | Function values converge uniformly across domain | Convergence in norm, stronger than weak convergence |
| Key Property | Preserves continuity and integrals under limit | Preserves limit in norm topology, ensures closeness in vector space |
| Relation to Other Convergences | Implies pointwise convergence but not vice versa | Implies weak convergence but not vice versa |
| Examples | Sequence of continuous functions converging uniformly to a continuous function | Sequence in L^2 space converging strongly to a function |
Introduction to Convergence in Analysis
Uniform convergence ensures that a sequence of functions converges to a limit function at the same rate across the entire domain, preserving continuity and integrability properties. Strong convergence, often used in functional analysis, relates to convergence in norm within a metric space, implying convergence in magnitude but not necessarily uniform behavior. Understanding the distinctions between uniform and strong convergence is crucial for analyzing function spaces and ensuring the validity of limit operations in mathematical analysis.
Defining Uniform Convergence
Uniform convergence occurs when a sequence of functions converges to a limit function such that the speed of convergence is uniform across the entire domain, meaning the maximum difference between the functions and the limit function approaches zero as the sequence progresses. This contrasts with pointwise convergence, where convergence speed may vary at different points. Uniform convergence guarantees preservation of continuity and integrability properties, essential in mathematical analysis and functional spaces.
Understanding Strong Convergence
Strong convergence in functional analysis refers to a sequence of functions converging to a limit function such that the norm of their difference tends to zero, ensuring pointwise convergence and control over the overall function behavior in a normed space. Unlike uniform convergence, which requires convergence to be uniform across the entire domain, strong convergence emphasizes convergence in the norm, typically in spaces like L^p or Hilbert spaces. This concept is crucial in understanding the stability and approximation properties of function sequences in applied mathematics and quantum mechanics.
Core Differences Between Uniform and Strong Convergence
Uniform convergence requires a sequence of functions to converge to a limit function uniformly over the entire domain, ensuring the supremum of the absolute differences goes to zero. Strong convergence, often used in Hilbert or Banach spaces, means convergence in norm, where the norm of the difference between sequence elements and the limit tends to zero. The core difference lies in uniform convergence controlling pointwise behavior uniformly, while strong convergence measures convergence with respect to a space's norm structure, often allowing pointwise discrepancies if the norms vanish.
Mathematical Criteria for Uniform Convergence
Uniform convergence requires that for every e > 0, there exists an N such that for all n >= N and every point x in the domain, the inequality |f_n(x) - f(x)| < e holds uniformly. This means the supremum norm ||f_n - f|| = sup_x |f_n(x) - f(x)| converges to zero as n approaches infinity. Uniform convergence preserves continuity and integrability, distinguishing it from pointwise or strong convergence where convergence may depend on individual points.
Conditions and Examples of Strong Convergence
Strong convergence requires that a sequence of random variables \(X_n\) converges to \(X\) almost surely, meaning \(P(\lim_{n \to \infty} X_n = X) = 1\), which is a stricter condition than uniform convergence in norm. Conditions for strong convergence include the presence of dominated convergence or martingale convergence theorems ensuring almost sure convergence under certain boundedness or integrability assumptions. An example is the sequence defined by \(X_n = \frac{1}{n}Z\), where \(Z\) is a fixed random variable, which converges strongly to zero since \(X_n \to 0\) almost surely.
Implications in Functional Analysis
Uniform convergence implies strong convergence in normed vector spaces, ensuring that a sequence of functions converges uniformly to a limit function, preserving continuity and integrability properties crucial in functional analysis. Strong convergence, defined by convergence in norm, does not guarantee uniform convergence but ensures that limit function approximations are accurate in terms of the norm topology, which is vital for operator theory and Hilbert space applications. Understanding these convergence types impacts the study of bounded linear operators, spectral theory, and the stability of functional sequences within Banach and Hilbert spaces.
Applications in Real and Functional Spaces
Uniform convergence ensures that a sequence of functions converges to a limiting function uniformly on its entire domain, making it crucial for preserving properties like continuity and integrability in real analysis and functional spaces. Strong convergence, often defined in normed vector spaces such as Hilbert or Banach spaces, guarantees convergence in norm, which is fundamental for solving PDEs, optimization problems, and variational methods where stability of solutions is required. Applications in real and functional spaces leverage uniform convergence for consistency in approximation theory, while strong convergence underpins robustness in iterative algorithms and spectral theory.
Common Misconceptions and Pitfalls
Uniform convergence ensures that a sequence of functions converges uniformly to a limit function across the entire domain, whereas strong convergence relates to convergence in a norm on function spaces, typically in L2 or Hilbert spaces. A common misconception is assuming uniform convergence implies strong convergence or vice versa, ignoring the significant differences in their definitions and implications on limit interchangeability and continuity preservation. Another pitfall is neglecting that uniform convergence guarantees preservation of continuity, but strong convergence, especially in Lp spaces, does not ensure pointwise or uniform convergence, leading to errors in functional analysis and approximation theory.
Summary and Key Takeaways
Uniform convergence ensures that a sequence of functions converges to a limiting function at the same rate across the entire domain, preserving continuity and integrability properties. Strong convergence, often used in functional analysis and Hilbert spaces, implies convergence in norm but does not guarantee uniform closeness pointwise. Key takeaways highlight uniform convergence's role in maintaining function behavior globally, while strong convergence focuses on convergence in the underlying space's metric or norm.
Uniform convergence Infographic
 libterm.com
libterm.com