A Borel set is a fundamental concept in measure theory and topology, defined as any set that can be formed from open or closed sets through countable unions, intersections, and complements. These sets form the Borel sigma-algebra, which plays a crucial role in defining measurable spaces and integrating functions in real analysis. Discover how understanding Borel sets is essential for exploring advanced mathematical concepts in the rest of this article.
Table of Comparison
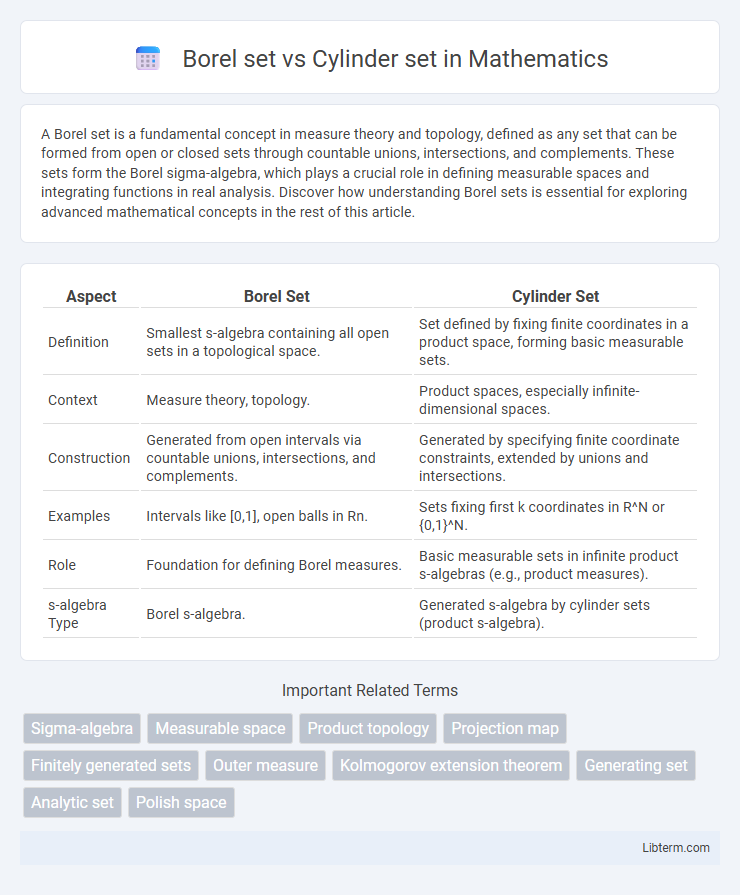
| Aspect | Borel Set | Cylinder Set |
|---|---|---|
| Definition | Smallest s-algebra containing all open sets in a topological space. | Set defined by fixing finite coordinates in a product space, forming basic measurable sets. |
| Context | Measure theory, topology. | Product spaces, especially infinite-dimensional spaces. |
| Construction | Generated from open intervals via countable unions, intersections, and complements. | Generated by specifying finite coordinate constraints, extended by unions and intersections. |
| Examples | Intervals like [0,1], open balls in Rn. | Sets fixing first k coordinates in R^N or {0,1}^N. |
| Role | Foundation for defining Borel measures. | Basic measurable sets in infinite product s-algebras (e.g., product measures). |
| s-algebra Type | Borel s-algebra. | Generated s-algebra by cylinder sets (product s-algebra). |
Introduction to Borel Sets and Cylinder Sets
Borel sets are the s-algebra generated by open sets in a topological space, serving as the fundamental building blocks for measurable spaces in probability and analysis. Cylinder sets are basic measurable sets in product spaces, defined by fixing finitely many coordinates and allowing others to vary freely, crucial for studying infinite-dimensional spaces and stochastic processes. The interplay between Borel sets and cylinder sets underpins measure theory by enabling the extension of measures from simple to complex spaces.
Defining Borel Sets
Borel sets are generated through the smallest s-algebra containing all open sets in a given topological space, commonly the real line, making them fundamental in measure theory and probability. Cylinder sets, defined as preimages of measurable rectangles under coordinate projections in product spaces, serve as building blocks for product s-algebras. While Borel sets encompass a wide range of measurable subsets, cylinder sets specifically facilitate the construction of measures on infinite-dimensional spaces.
Understanding Cylinder Sets
Cylinder sets form the basis for defining topologies in product spaces, particularly in infinite-dimensional settings, where each cylinder set fixes values on a finite number of coordinates while leaving others arbitrary. They differ from Borel sets, which arise from the s-algebra generated by open sets in a topological space, by their constructive role in building measurable structures on function spaces or sequences. Understanding cylinder sets is crucial for studying measures on infinite product spaces, as they enable the extension of finite-dimensional intuitions to infinite dimensions.
Construction of Borel Sets
Borel sets are constructed from open sets in a topological space through countable operations such as unions, intersections, and complements, forming the smallest s-algebra containing all open sets. Cylinder sets are basic building blocks in product spaces, defined as sets depending on finitely many coordinates, often generating the product s-algebra. The construction of Borel sets involves iterative application of s-algebra operations starting from open sets, while cylinder sets serve as generators for s-algebras in infinite-dimensional spaces.
Generation of Cylinder Sets
Cylinder sets are generated by fixing coordinates in product spaces, serving as fundamental building blocks in infinite-dimensional analysis and probability theory. Borel sets, derived from the Borel s-algebra on topological spaces, include all open and closed sets and are generated by countable unions and intersections of these basis elements. The generation of cylinder sets relies on finite-dimensional projections that induce a s-algebra smaller than or equal to the Borel s-algebra on infinite product spaces.
Key Differences Between Borel and Cylinder Sets
Borel sets are generated from open sets through countable unions, intersections, and complements within a topological space, forming a sigma-algebra essential in measure theory. Cylinder sets, defined in product spaces, depend on finitely many coordinates and generate the product sigma-algebra, serving as basic building blocks for measures on infinite-dimensional spaces. The key difference lies in Borel sets' construction based on a topology, while cylinder sets arise from finite-dimensional projections in product spaces.
Applications of Borel Sets in Measure Theory
Borel sets form the foundation of measurable spaces in measure theory and allow the construction of Borel measures crucial for probability, integration, and real analysis. Cylinder sets, often used in product spaces and infinite-dimensional settings, generate sigma-algebras that approximate Borel sigma-algebras on function spaces. Applications of Borel sets include defining Lebesgue measure, facilitating measurable functions, and enabling rigorous probability distributions on real-valued random variables.
Uses of Cylinder Sets in Probability Spaces
Cylinder sets serve as foundational building blocks in defining probability measures on infinite-dimensional product spaces by specifying events determined by finitely many coordinates. Unlike Borel sets, which are generated from open sets in topological spaces and are widely used in real analysis, cylinder sets facilitate the construction of sigma-algebras in stochastic processes such as Brownian motion or Markov chains. Their use ensures measurable structure in complex spaces where direct application of Borel sets is challenging, enabling rigorous treatment of probabilities in infinite-dimensional settings.
Relationships Between Borel and Cylinder Sets
Borel sets form the s-algebra generated by open sets in a topological space, encompassing all measurable events relevant in analysis and probability theory. Cylinder sets are special subsets defined in product spaces, generated by fixing finite coordinates and open sets, serving as building blocks for product s-algebras. The relationship between Borel and cylinder sets lies in the fact that the s-algebra generated by cylinder sets in infinite-dimensional spaces coincides with the Borel s-algebra of the product topology, ensuring measurable structure compatibility across finite-dimensional projections and infinite-dimensional contexts.
Summary and Implications in Mathematical Analysis
Borel sets, generated by open sets through countable unions, intersections, and complements, form a fundamental s-algebra in topology and measure theory, enabling the rigorous definition of measures like the Lebesgue measure. Cylinder sets, constructed from finite-dimensional projections in infinite-dimensional spaces, serve as building blocks for product s-algebras, playing a crucial role in stochastic processes and functional analysis. Understanding the distinction and interplay between Borel and cylinder sets allows for precise handling of measurability and integration in both finite and infinite-dimensional contexts, impacting probability theory and advanced analysis.
Borel set Infographic
 libterm.com
libterm.com