The fppf topology, short for "faithfully flat and finitely presented," is a Grothendieck topology used in algebraic geometry to study sheaves and descent theory on schemes. It refines the flat topology by imposing the additional condition that morphisms be finitely presented, ensuring better control over algebraic structures. Explore the rest of this article to understand how the fppf topology plays a crucial role in modern algebraic geometry and your research.
Table of Comparison
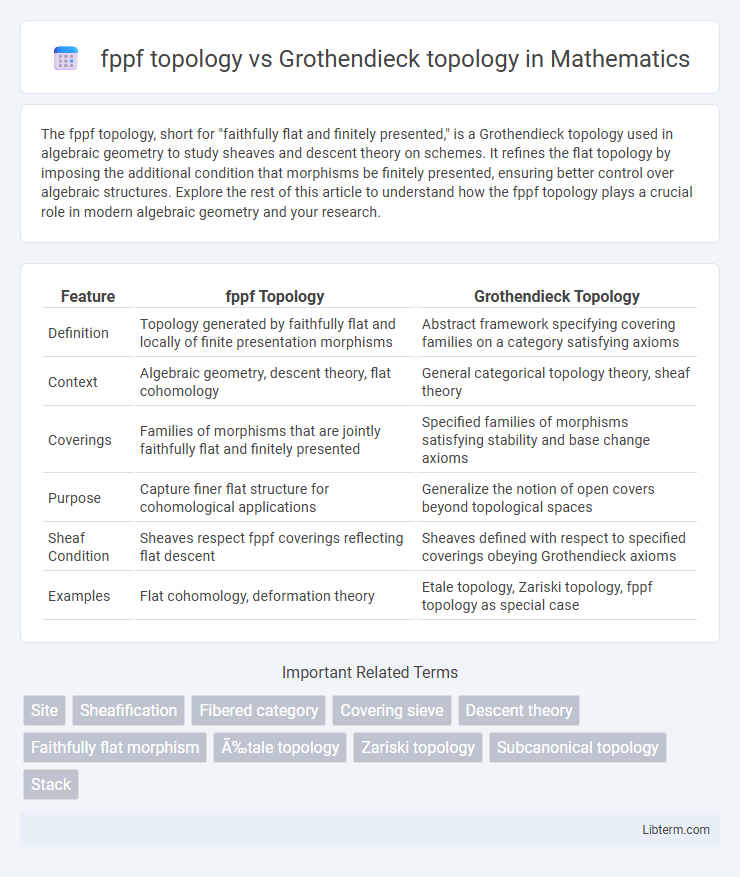
| Feature | fppf Topology | Grothendieck Topology |
|---|---|---|
| Definition | Topology generated by faithfully flat and locally of finite presentation morphisms | Abstract framework specifying covering families on a category satisfying axioms |
| Context | Algebraic geometry, descent theory, flat cohomology | General categorical topology theory, sheaf theory |
| Coverings | Families of morphisms that are jointly faithfully flat and finitely presented | Specified families of morphisms satisfying stability and base change axioms |
| Purpose | Capture finer flat structure for cohomological applications | Generalize the notion of open covers beyond topological spaces |
| Sheaf Condition | Sheaves respect fppf coverings reflecting flat descent | Sheaves defined with respect to specified coverings obeying Grothendieck axioms |
| Examples | Flat cohomology, deformation theory | Etale topology, Zariski topology, fppf topology as special case |
Introduction to Grothendieck Topologies
Grothendieck topologies generalize classical topologies by defining coverings through families of morphisms rather than open sets, providing a flexible framework for sheaf theory in algebraic geometry. The fppf (faithfully flat and finitely presented) topology is a specific type of Grothendieck topology where coverings consist of faithfully flat morphisms of finite presentation, capturing flat descent properties essential for studying schemes. This approach enables a richer understanding of geometric objects beyond open set coverings, facilitating the development of cohomological methods and descent theory in modern algebraic geometry.
Overview of the fppf Topology
The fppf topology is a specific type of Grothendieck topology used in algebraic geometry, defined by faithfully flat morphisms of finite presentation. This topology refines the fpqc topology by imposing finite presentation conditions, enabling more manageable descent theory and cohomological computations. It is central to studying sheaves, descent, and deformation problems on schemes due to its balance between flatness and finiteness constraints.
Fundamental Concepts: Coverings and Sheaves
The fppf topology, defined by faithfully flat and finitely presented morphisms, refines the Grothendieck topology by emphasizing flatness and finite presentation in its coverings, thus allowing a finer control of descent data. In both topologies, coverings serve as families of morphisms providing local data patches, while sheaves are contravariant functors that satisfy the gluing condition relative to these coverings, ensuring consistent local-to-global properties. The pivotal distinction lies in the nature of the coverings: the Grothendieck topology may employ broader classes of morphisms, whereas the fppf topology restricts to flat morphisms that preserve specific algebraic structures, enhancing the behavior of sheaves in algebraic geometry.
Motivation Behind the fppf Topology
The fppf topology was motivated by the need to study faithfully flat morphisms of finite presentation, enabling finer descent theory and better control over algebraic structures in schemes. Unlike general Grothendieck topologies, the fppf topology emphasizes flatness and finite presentation to capture subtle geometric and algebraic phenomena that other topologies, such as the etale or Zariski topology, might miss. This focus facilitates applications in deformation theory, moduli problems, and descent for quasi-coherent sheaves, enhancing the toolkit available for modern algebraic geometry.
Comparing Zariski, Étale, and fppf Topologies
The Zariski topology, based on open subsets defined by vanishing of functions, is coarser and less sensitive to subtle geometric properties than the finer etale and fppf topologies, which reflect more intricate algebraic structures through covering families of flat morphisms. The etale topology uses etale morphisms that are flat, unramified, and of finite presentation, capturing local isomorphisms and allowing one to study phenomena like fundamental groups and cohomology with better fineness than Zariski. The fppf topology generalizes further by considering faithfully flat morphisms locally of finite presentation, accommodating more general coverings and enabling descent theory for broader classes of sheaves and algebraic stacks, therefore serving as an intermediate refinement between Zariski and fppf topologies in terms of generality and geometric subtlety.
Core Differences: fppf vs Grothendieck Topology
The fppf topology, a specific case of Grothendieck topologies, is defined by faithfully flat morphisms locally of finite presentation, emphasizing flatness and finite presentation conditions to capture finer covering families in algebraic geometry. Grothendieck topology, more broadly, generalizes classical topologies through the concept of sieves and covers, allowing a flexible framework to define sheaves on arbitrary categories. Core differences lie in the nature of their coverings: fppf topology uses morphisms with algebraic flatness and finiteness constraints, while Grothendieck topology abstracts covering data without restricting to specific morphism properties.
Role of Flatness and Faithfully Flat Morphisms
The fppf topology is a Grothendieck topology on the category of schemes defined using faithfully flat and locally of finite presentation morphisms, emphasizing the role of flatness to ensure effective descent properties for quasi-coherent sheaves and modules. Flatness guarantees that the pullback functor preserves exact sequences while faithful flatness ensures surjectivity on the underlying topological spaces, enabling robust gluing of data. In contrast, Grothendieck topologies encompass a broader framework of covering families, but the fppf topology specifically leverages flatness conditions to control the behavior of morphisms under base change and to facilitate descent theory in algebraic geometry.
Applications of the fppf Topology in Algebraic Geometry
The fppf topology, characterized by faithfully flat and locally of finite presentation morphisms, plays a crucial role in algebraic geometry by enabling the study of descent theory and the construction of moduli spaces. It facilitates the classification of principal bundles and works effectively in contexts where etale or Zariski topologies are insufficient, especially in handling non-noetherian schemes or infinitesimal extensions. Applications include the definition of algebraic stacks, cohomological descent, and the analysis of flat cohomology groups crucial for understanding deformation theory and arithmetic geometry.
Advantages and Limitations of the fppf Topology
The fppf topology, a Grothendieck topology defined by faithfully flat and finitely presented morphisms, provides advantages such as better handling of non-smooth and non-etale morphisms, making it well-suited for descent theory and deformation problems in algebraic geometry. Its limitations include greater technical complexity and reduced manageability compared to finer topologies like the etale topology, often resulting in more intricate covering families and challenges in computation. While the fppf topology excels in broader generality, it may be less intuitive and harder to apply in practice due to its reliance on flatness conditions and intricate local behavior.
Conclusion: The fppf Topology in the Landscape of Grothendieck Topologies
The fppf topology, characterized by faithfully flat and finitely presented morphisms, occupies a crucial niche within Grothendieck topologies by balancing generality and tractability in descent theory. It refines the fpqc topology while enabling effective treatment of schemes and algebraic stacks, especially in algebraic geometry and number theory. Its role enhances the toolkit for sheaf theory and cohomological methods, positioning it as a versatile and indispensable structure in modern algebraic frameworks.
fppf topology Infographic
 libterm.com
libterm.com