Almost everywhere convergence describes a sequence of functions converging at every point except on a set of measure zero, ensuring practical consistency in various fields like probability and analysis. This concept is crucial in understanding the behavior of functions under limits in real-world applications where perfect convergence is too strict. Explore the article to deepen your grasp of almost everywhere convergence and its significance in mathematical analysis.
Table of Comparison
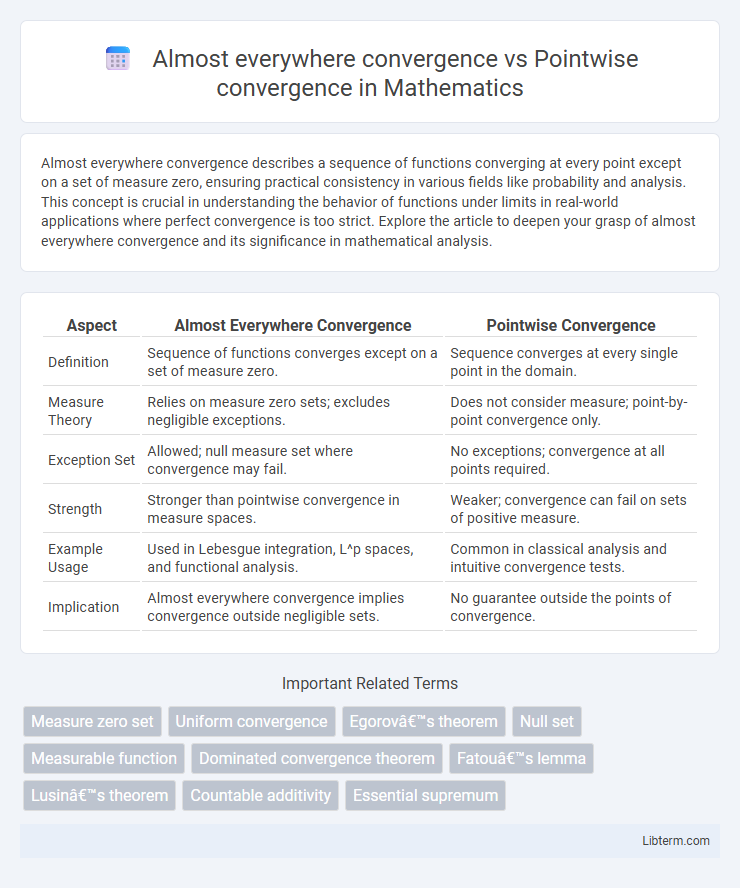
| Aspect | Almost Everywhere Convergence | Pointwise Convergence |
|---|---|---|
| Definition | Sequence of functions converges except on a set of measure zero. | Sequence converges at every single point in the domain. |
| Measure Theory | Relies on measure zero sets; excludes negligible exceptions. | Does not consider measure; point-by-point convergence only. |
| Exception Set | Allowed; null measure set where convergence may fail. | No exceptions; convergence at all points required. |
| Strength | Stronger than pointwise convergence in measure spaces. | Weaker; convergence can fail on sets of positive measure. |
| Example Usage | Used in Lebesgue integration, L^p spaces, and functional analysis. | Common in classical analysis and intuitive convergence tests. |
| Implication | Almost everywhere convergence implies convergence outside negligible sets. | No guarantee outside the points of convergence. |
Introduction to Sequence Convergence in Analysis
Almost everywhere convergence occurs when a sequence of functions converges at all points except for a set of measure zero, providing a stronger notion than pointwise convergence, which only requires convergence at each individual point without measure considerations. In analysis, understanding these modes of convergence is fundamental for studying function limits and their behavior in Lebesgue spaces. Almost everywhere convergence is crucial in real analysis and probability theory, where functions may converge outside negligible exceptions, unlike pointwise convergence which may fail to respect measure structures.
Defining Pointwise Convergence
Pointwise convergence of a sequence of functions {f_n} to a function f occurs when, for every point x in the domain, the sequence {f_n(x)} converges to f(x) as n approaches infinity. This means that for each fixed x, given any e > 0, there exists an N such that for all n > N, |f_n(x) - f(x)| < e holds. Pointwise convergence does not require uniform behavior across the domain, distinguishing it from stronger forms like uniform convergence and almost everywhere convergence.
Understanding Almost Everywhere Convergence
Almost everywhere convergence refers to a sequence of functions converging at all points in a domain except for a set of measure zero, making it a stronger concept than pointwise convergence, which requires convergence at every single point without exception. Understanding almost everywhere convergence is crucial in measure theory and functional analysis because it ensures convergence for "almost all" inputs, allowing the omission of pathological exceptions that have negligible impact on integrals or measure-based properties. This concept is foundational for the Lebesgue Dominated Convergence Theorem and other results where controlling convergence on sets of full measure is essential.
Key Differences Between Pointwise and Almost Everywhere Convergence
Pointwise convergence requires a sequence of functions to converge at every individual point within the domain, whereas almost everywhere convergence allows the sequence to converge except on a set of measure zero. This distinction is crucial in measure theory, where almost everywhere convergence guarantees convergence for almost all points, making it stronger in the context of integrable functions and Lebesgue measure spaces. Unlike pointwise convergence, almost everywhere convergence often aligns better with practical applications in real analysis and probability theory, as it tolerates negligible exceptions.
Mathematical Formalism of Both Convergence Types
Almost everywhere convergence of a sequence of functions \( \{f_n\} \) to a function \( f \) on a measure space \( (X, \mathcal{F}, \mu) \) means \( f_n(x) \to f(x) \) for all \( x \in X \) except on a set \( N \subseteq X \) with measure zero, \( \mu(N) = 0 \). Pointwise convergence requires \( f_n(x) \to f(x) \) to hold for every point \( x \in X \) without exception. The distinction lies in measure-theoretic null sets, where almost everywhere convergence permits deviations on a null set while pointwise convergence admits none.
Illustrative Examples: Pointwise vs. Almost Everywhere
Pointwise convergence occurs when a sequence of functions converges at every individual point in the domain, while almost everywhere convergence means convergence happens at every point except for a set of measure zero. For example, the sequence of functions f_n(x) = x^n on [0,1] converges pointwise to a function that is zero for all x in [0,1), but equals one at x=1; this demonstrates pointwise but not uniform convergence. In contrast, a sequence defined by f_n(x) = 1 if x is rational and n>=1, 0 otherwise, converges to zero almost everywhere since the rationals have measure zero, showing convergence almost everywhere but not pointwise everywhere.
Implications in Measure Theory and Real Analysis
Almost everywhere convergence implies pointwise convergence except on a set of measure zero, making it a stronger condition in measure theory for handling functions in Lp spaces. Pointwise convergence alone does not guarantee integrability or preservation of measure-theoretic properties, whereas almost everywhere convergence ensures that limit functions retain measurability and integrability almost surely. This distinction underpins key theorems like the Dominated Convergence Theorem and Egorov's Theorem, which facilitate rigorous analysis of function limits in real analysis.
Common Misconceptions and Pitfalls
Almost everywhere convergence and pointwise convergence are often confused due to their similar definitions but differ significantly in measure-theoretic contexts. A common misconception is to assume pointwise convergence guarantees almost everywhere convergence, ignoring that pointwise convergence allows divergence on sets of positive measure. Pitfalls include overlooking null sets where almost everywhere convergence may fail, leading to incorrect conclusions in functional analysis and probability theory.
Practical Applications and Use Cases
Almost everywhere convergence ensures that a sequence of functions converges at every point except a set of measure zero, which is crucial in probability theory and signal processing where exceptions on negligible sets do not affect overall outcomes. Pointwise convergence, though simpler, can fail to guarantee stability in practical applications like numerical analysis and machine learning, where consistent behavior across nearly all inputs is required. In ergodic theory, almost everywhere convergence aids in deriving meaningful long-term averages from dynamical systems that would be unreliable under mere pointwise convergence.
Summary: Choosing the Right Convergence Notion
Almost everywhere convergence requires that a sequence of functions converges at all points except for a set of measure zero, making it particularly useful in measure-theoretic contexts and integration theory. Pointwise convergence demands convergence at every single point, but it can be sensitive to variations on sets of measure zero, limiting its applicability in integrable function spaces. Selecting between these notions depends on the measure space involved and the desired analytical properties, with almost everywhere convergence often preferred for Lebesgue integrals and practical applications in probability and ergodic theory.
Almost everywhere convergence Infographic
 libterm.com
libterm.com