Algebraic geometry explores the intricate relationship between algebraic equations and geometric structures, revealing deep insights into shapes defined by polynomial equations. This mathematical field combines techniques from abstract algebra, especially commutative algebra, with geometric intuition to solve problems ranging from curve classification to higher-dimensional varieties. Discover how your understanding can expand by diving into the fascinating concepts and applications detailed in the rest of this article.
Table of Comparison
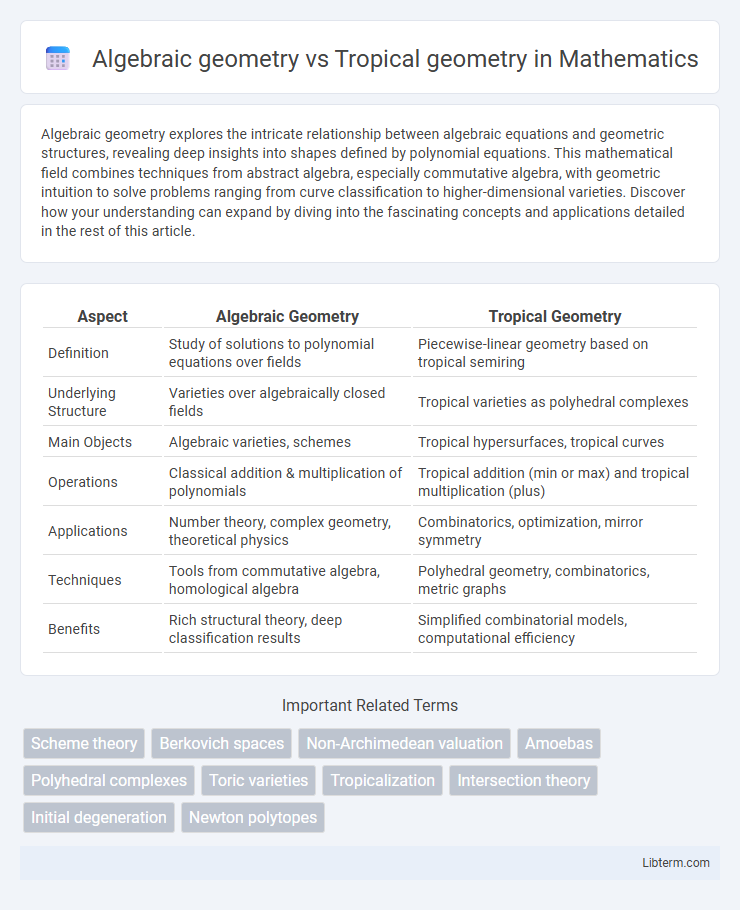
| Aspect | Algebraic Geometry | Tropical Geometry |
|---|---|---|
| Definition | Study of solutions to polynomial equations over fields | Piecewise-linear geometry based on tropical semiring |
| Underlying Structure | Varieties over algebraically closed fields | Tropical varieties as polyhedral complexes |
| Main Objects | Algebraic varieties, schemes | Tropical hypersurfaces, tropical curves |
| Operations | Classical addition & multiplication of polynomials | Tropical addition (min or max) and tropical multiplication (plus) |
| Applications | Number theory, complex geometry, theoretical physics | Combinatorics, optimization, mirror symmetry |
| Techniques | Tools from commutative algebra, homological algebra | Polyhedral geometry, combinatorics, metric graphs |
| Benefits | Rich structural theory, deep classification results | Simplified combinatorial models, computational efficiency |
Introduction to Algebraic Geometry and Tropical Geometry
Algebraic geometry explores solutions to polynomial equations using concepts from abstract algebra and geometry, focusing on varieties, schemes, and their intrinsic properties over fields. Tropical geometry translates classical algebraic varieties into piecewise-linear objects using the tropical semiring, enabling combinatorial and computational approaches to traditionally complex problems. Both fields intersect, with tropical geometry providing a simplified, discrete framework for studying the rich structures found in algebraic geometry.
Fundamental Concepts in Algebraic Geometry
Algebraic geometry studies solutions to polynomial equations using concepts like varieties, schemes, and morphisms, emphasizing structure over algebraically closed fields. It leverages ideals and coordinate rings to analyze geometric objects in a classical and scheme-theoretic framework. Tropical geometry translates these into combinatorial objects through piecewise-linear geometry, enabling the study of algebraic varieties via polyhedral complexes and valuations.
Core Principles of Tropical Geometry
Tropical geometry transforms classical algebraic varieties into piecewise-linear objects by replacing addition with minimum or maximum operations and multiplication with addition, creating a combinatorial shadow of algebraic geometry. Core principles include the tropical semiring structure, valuation maps linking algebraic varieties to their tropical counterparts, and the correspondence between tropical varieties and polyhedral fans. This framework simplifies complex geometric problems by leveraging piecewise-linear methods, enabling novel insights into intersection theory, enumerative geometry, and optimization.
Comparing Algebraic and Tropical Geometric Objects
Algebraic geometry studies solutions of polynomial equations over fields, emphasizing varieties with rich structural properties defined by polynomial ideals. Tropical geometry translates these classical varieties into piecewise-linear combinatorial objects called tropical varieties, capturing essential geometric and combinatorial features via the tropical semiring. Comparing algebraic and tropical geometric objects reveals that tropicalization preserves fundamental invariants like dimension and intersection multiplicity while simplifying complex algebraic structures into polyhedral complexes amenable to computational and combinatorial analysis.
Methods and Tools in Both Geometries
Algebraic geometry utilizes polynomial equations and schemes to study the solutions of systems in algebraic varieties, relying heavily on tools such as sheaf theory, cohomology, and complex analysis. Tropical geometry simplifies classical algebraic varieties into combinatorial objects called tropical varieties using piecewise-linear structures and tools like valuation maps, polyhedral complexes, and max-plus algebra. Both fields employ techniques from computational algebra but differ in their core methods, with algebraic geometry focusing on continuous methods and tropical geometry emphasizing discrete and combinatorial approaches.
Applications in Mathematics and Beyond
Algebraic geometry offers powerful tools for solving polynomial equations and studying geometric structures over complex numbers, underpinning advancements in number theory, cryptography, and string theory. Tropical geometry simplifies these problems by using combinatorial techniques and piecewise-linear structures, enabling applications in optimization, phylogenetics, and economics. Both fields contribute to mathematical modeling, with tropical geometry providing computational efficiency and algebraic geometry offering deep theoretical insights.
Intersection Theory: Classical vs Tropical Perspectives
Intersection theory in algebraic geometry studies the intersection multiplicities of algebraic varieties using tools like Chow rings and cohomology classes to capture intricate geometric information. Tropical geometry translates these concepts into a combinatorial framework, representing varieties as polyhedral complexes where intersection theory operates through balancing conditions and stable intersections of tropical cycles. This tropical perspective simplifies complex algebraic interactions into piecewise-linear geometry, enabling effective computation of intersection numbers while preserving essential geometric properties.
Computational Aspects: Algorithms and Efficiency
Algebraic geometry employs complex polynomial equations to study geometric structures, relying on symbolic computation algorithms like Grobner bases for solving systems of polynomial ideals, which can be computationally intensive due to their high complexity. Tropical geometry simplifies these problems by transforming algebraic structures into piecewise-linear combinatorial objects, allowing for faster algorithms and greater efficiency in computations such as solving optimization problems and enumerating solutions. Tropical methods often reduce computational overhead through linear programming techniques, enabling practical explorations in cases where algebraic geometry's symbolic calculations become infeasible.
Recent Advances and Research Directions
Recent advances in algebraic geometry have deepened the understanding of moduli spaces and birational geometry through the study of derived categories and mirror symmetry. Tropical geometry has emerged as a powerful combinatorial tool for solving classical problems by translating complex algebraic varieties into polyhedral complexes, enabling new computational techniques and insights in enumerative geometry. Current research directions focus on bridging these fields by developing tropical methods for non-Archimedean analytic spaces and extending tropical intersection theory to better understand degenerations and mirror symmetry phenomena.
Future Prospects and Challenges in Both Fields
Algebraic geometry faces challenges in computational complexity and extending its techniques to higher-dimensional varieties, prompting research in algorithmic approaches and applications to number theory and physics. Tropical geometry offers promising advancements in combinatorial optimization and mirror symmetry but requires further development to fully connect classical geometric intuition with tropical methods. Both fields hold future prospects in interdisciplinary collaboration, with potential breakthroughs in understanding moduli spaces, non-Archimedean analysis, and integrable systems.
Algebraic geometry Infographic
 libterm.com
libterm.com