Regular sets are fundamental concepts in automata theory, representing collections of strings defined by regular expressions or finite automata. Understanding their properties helps in designing efficient pattern matching algorithms and formal language analysis. Explore this article to deepen your knowledge about regular sets and their practical applications.
Table of Comparison
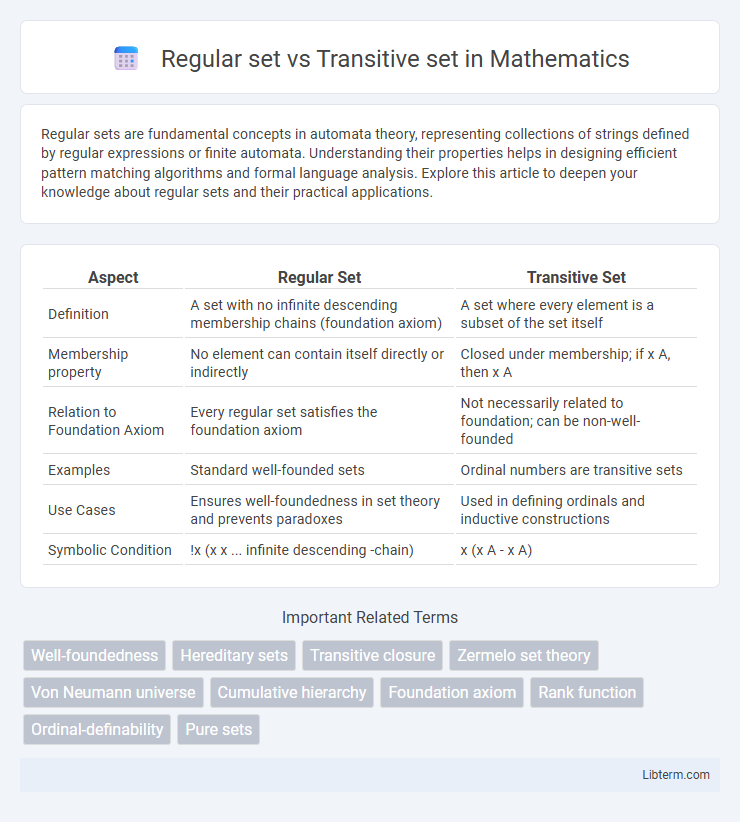
| Aspect | Regular Set | Transitive Set |
|---|---|---|
| Definition | A set with no infinite descending membership chains (foundation axiom) | A set where every element is a subset of the set itself |
| Membership property | No element can contain itself directly or indirectly | Closed under membership; if x A, then x A |
| Relation to Foundation Axiom | Every regular set satisfies the foundation axiom | Not necessarily related to foundation; can be non-well-founded |
| Examples | Standard well-founded sets | Ordinal numbers are transitive sets |
| Use Cases | Ensures well-foundedness in set theory and prevents paradoxes | Used in defining ordinals and inductive constructions |
| Symbolic Condition | !x (x x ... infinite descending -chain) | x (x A - x A) |
Introduction to Regular and Transitive Sets
Regular sets consist of elements with properties that prevent infinite descending membership chains, ensuring foundational well-foundedness in set theory. Transitive sets contain all elements of their elements, establishing a hierarchical structure where membership is inherited through elements. Understanding these distinctions is crucial for analyzing set-theoretic constructions and models.
Defining Regular Sets
Regular sets are collections of elements defined by a well-founded membership relation, ensuring no infinite descending chains exist, which guarantees the set's construction from the empty set through finite iterative steps. These sets satisfy the axiom of regularity, meaning every non-empty set contains an element disjoint from itself, preventing self-containing loops. In contrast, transitive sets require every element to be a subset of the set itself, emphasizing closure under membership rather than the foundational hierarchy.
Understanding Transitive Sets
Transitive sets are fundamental in set theory, characterized by the property that every element of the set is also a subset of the set, ensuring the set is closed under membership. Unlike regular sets that do not necessarily maintain this closure, transitive sets facilitate the construction of ordinal numbers and the cumulative hierarchy in Zermelo-Fraenkel set theory. Understanding transitive sets is crucial for grasping foundational concepts like rank functions and well-foundedness in mathematical logic.
Key Differences Between Regular and Transitive Sets
Regular sets require every element to have a well-founded membership structure with no infinite descending chains, ensuring no element belongs to itself indirectly. Transitive sets contain all elements of their elements, meaning if an element belongs to a member of the set, it also belongs directly to the set. The key difference lies in regular sets emphasizing foundation and well-foundedness, while transitive sets emphasize closure under element membership.
Properties of Regular Sets
Regular sets in set theory are collections of sets closed under well-foundedness, meaning every non-empty subset has an -minimal element, preventing infinite descending -chains. These sets satisfy the axiom of regularity (foundation), ensuring no set is a member of itself directly or indirectly, which guarantees a hierarchical, well-founded structure. This property contrasts with transitive sets that require every element of the set to be a subset of the set, emphasizing different foundational behaviors in set construction.
Properties of Transitive Sets
Transitive sets possess the property that every element of the set is also a subset of the set, meaning if an element x belongs to a transitive set T, then all elements of x also belong to T. This property ensures closure under the membership relation and distinguishes transitive sets from regular sets, which do not require such closure. Transitive sets are fundamental in set theory, especially in constructing ordinals and modeling well-founded structures.
Examples of Regular Sets
Regular sets are collections of elements that are well-defined by finitely many steps, often characterized by closure properties under operations like union, concatenation, and Kleene star. For example, the set of all strings over {a, b} containing an even number of a's or the set of binary strings ending with '01' are regular sets recognized by finite automata. Regular expressions such as (ab)* or a(b|c)*d precisely describe these regular sets, enabling efficient pattern matching and validation in computational tasks.
Examples of Transitive Sets
A transitive set is defined by the property that every element of the set is also a subset of the set, such as the set \( \{ \emptyset, \{\emptyset\} \} \), where both elements are subsets. Another example includes \( \{ \emptyset, \{\emptyset\}, \{\emptyset, \{\emptyset\}\} \} \), which contains all elements of its elements, demonstrating the transitive property. In contrast, a regular set does not require this subset inclusion condition, often making transitive sets essential in set theory for constructing ordinal numbers.
Applications in Set Theory
Regular sets are essential in set theory for constructing well-founded models, ensuring no infinite descending membership chains, which is critical in proving foundational theorems. Transitive sets, containing all elements of their elements, facilitate hierarchies like the cumulative hierarchy (Va), instrumental in defining rank and ordinals. Applications of regular and transitive sets intersect in developing models of ZFC, where transitive sets serve as stages and regularity supports foundation axioms to avoid paradoxes.
Conclusion: Comparing Regular and Transitive Sets
Regular sets avoid infinite descending membership chains, ensuring well-foundedness, while transitive sets contain all elements of their members, supporting closure properties. Regular sets are crucial for foundational set theory and avoiding paradoxes, whereas transitive sets facilitate the construction of cumulative hierarchies and ordinal analysis. The interplay between regularity and transitivity underpins many advanced concepts in set theory, highlighting their complementary roles in structuring mathematical universes.
Regular set Infographic
 libterm.com
libterm.com