Tensor algebra provides a powerful framework for manipulating tensors, objects that generalize scalars, vectors, and matrices to higher dimensions. This mathematical structure plays a vital role in physics, engineering, and computer science by enabling the representation and transformation of multidimensional data efficiently. Explore the rest of this article to deepen your understanding of tensor algebra and its practical applications in various fields.
Table of Comparison
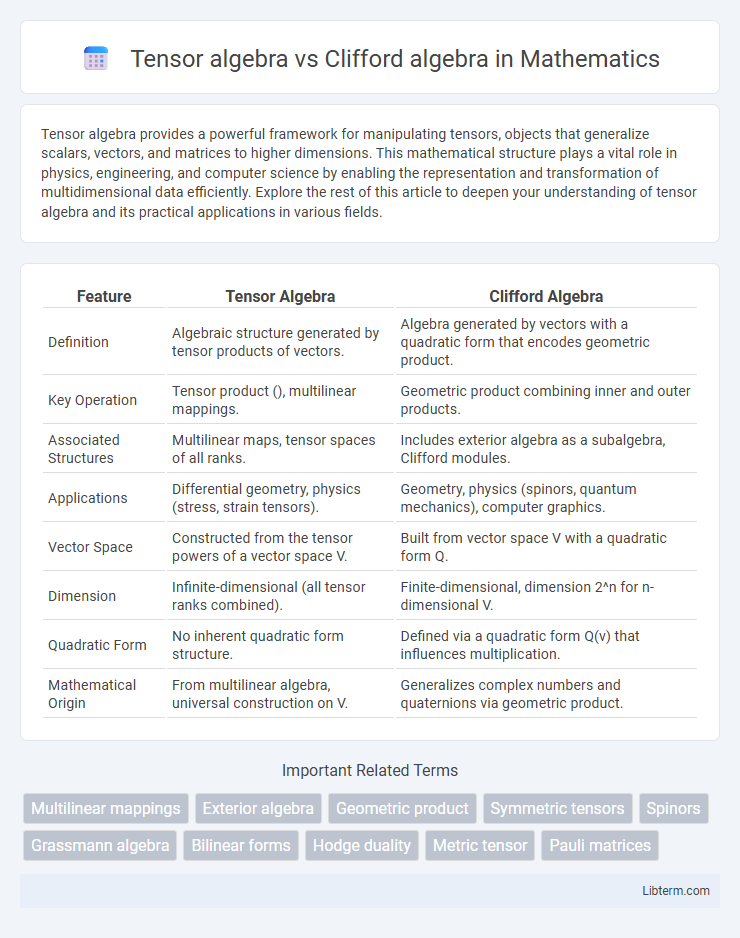
| Feature | Tensor Algebra | Clifford Algebra |
|---|---|---|
| Definition | Algebraic structure generated by tensor products of vectors. | Algebra generated by vectors with a quadratic form that encodes geometric product. |
| Key Operation | Tensor product (), multilinear mappings. | Geometric product combining inner and outer products. |
| Associated Structures | Multilinear maps, tensor spaces of all ranks. | Includes exterior algebra as a subalgebra, Clifford modules. |
| Applications | Differential geometry, physics (stress, strain tensors). | Geometry, physics (spinors, quantum mechanics), computer graphics. |
| Vector Space | Constructed from the tensor powers of a vector space V. | Built from vector space V with a quadratic form Q. |
| Dimension | Infinite-dimensional (all tensor ranks combined). | Finite-dimensional, dimension 2^n for n-dimensional V. |
| Quadratic Form | No inherent quadratic form structure. | Defined via a quadratic form Q(v) that influences multiplication. |
| Mathematical Origin | From multilinear algebra, universal construction on V. | Generalizes complex numbers and quaternions via geometric product. |
Introduction to Tensor Algebra and Clifford Algebra
Tensor algebra generalizes linear algebra by focusing on multilinear maps and tensor products, enabling the manipulation of tensors of varying orders to represent complex geometric and physical relationships. Clifford algebra extends tensor algebra by incorporating a quadratic form to define a geometric product, blending inner and outer products to encode rotations and reflections in vector spaces. The introduction to Clifford algebra highlights its applications in physics and computer graphics, offering a powerful extension to traditional tensor methods for modeling spatial transformations.
Mathematical Foundations and Definitions
Tensor algebra is founded on multilinear maps and tensor products defined over vector spaces, emphasizing the construction of tensors as multidimensional arrays that transform covariantly or contravariantly under coordinate changes. Clifford algebra extends tensor algebra by incorporating a quadratic form to introduce a geometric product, combining the inner (dot) and outer (wedge) products to model orthogonal transformations and encode geometric information. The mathematical foundation of Clifford algebra lies in generating an associative algebra from a vector space equipped with a bilinear form, providing a unified language for rotations, reflections, and metric structures beyond the purely multilinear framework of tensor algebra.
Key Structural Differences
Tensor algebra involves the construction of tensors through multilinear maps and is fundamentally based on operations like tensor products and contractions, emphasizing vector spaces and their duals. Clifford algebra extends tensor algebra by incorporating a quadratic form to define a geometric product, resulting in richer algebraic structures that unify scalars, vectors, and higher-grade elements. Key structural differences include the non-commutative and associative geometric product in Clifford algebra versus the generally commutative and linear operations in tensor algebra, enabling Clifford algebra to model geometric transformations and rotations more efficiently.
Notational and Conceptual Distinctions
Tensor algebra employs multi-index notation to represent tensors as multilinear maps, focusing on the manipulation of components under coordinate transformations. Clifford algebra integrates tensor algebra with a geometric product, combining inner and outer products into a single associative operation, enabling the representation of geometric transformations and reflections. Notationally, Clifford algebra introduces basis elements satisfying specific anticommutation relations, while tensor algebra uses indexed arrays without such algebraic constraints.
Algebraic Operations: Comparison and Contrast
Tensor algebra involves operations such as tensor product, contraction, and direct sum, enabling manipulation of multidimensional arrays with components indexed by multiple variables. Clifford algebra extends tensor algebra by incorporating a geometric product that combines inner and outer products, allowing representation of rotations and reflections within a unified algebraic framework. Unlike tensor algebra, Clifford algebra's non-commutative multiplication encodes geometric transformations naturally, providing a more expressive structure for applications in physics and computer graphics.
Representing Geometry and Physical Quantities
Tensor algebra provides a framework for representing geometric and physical quantities through multi-linear maps and coordinate-independent transformations, enabling the manipulation of vectors, covectors, and higher-order tensors in Euclidean and non-Euclidean spaces. Clifford algebra extends tensor algebra by incorporating a geometric product that combines elements of inner and outer products, allowing for efficient representation and computation of rotations, reflections, and other geometric transformations in spaces with various metrics. This enhanced ability to encode geometric relationships makes Clifford algebra particularly powerful in physics, computer graphics, and robotics for modeling complex spatial phenomena and physical fields.
Applications in Physics and Engineering
Tensor algebra facilitates the manipulation of multi-dimensional arrays and is extensively used in continuum mechanics, general relativity, and stress-strain analysis in materials engineering. Clifford algebra extends tensor algebra by incorporating geometric product structures, enabling efficient descriptions of rotations, spinors, and electromagnetic fields in quantum mechanics and robotics. The combination of both algebras enhances computational methods in signal processing, computer vision, and theoretical physics modeling.
Computational Advantages and Challenges
Tensor algebra offers straightforward operations for multi-linear mappings and is widely supported in computational frameworks, making it efficient for high-dimensional data manipulation. Clifford algebra extends tensor algebra by incorporating geometric product operations, enabling more compact and expressive representations of rotations and reflections, which can simplify complex geometric computations. However, Clifford algebra's richer structure requires more intricate algorithms and higher computational overhead, posing challenges for implementation and optimization compared to tensor algebra's more established numerical methods.
Recent Developments and Research Trends
Recent developments in tensor algebra emphasize enhanced computational algorithms for high-dimensional data analysis and machine learning applications, leveraging multilinear maps and tensor decompositions to optimize performance. Clifford algebra research trends focus on geometric algebra frameworks, advancing applications in quantum computing, robotics, and computer vision through efficient representation of rotations and reflections. Emerging interdisciplinary approaches integrate tensor and Clifford algebras to address complex problems in physics and engineering, promoting novel algebraic structures and computational techniques.
Conclusion: Choosing the Right Algebraic Framework
Selecting the appropriate algebraic framework depends on the complexity of geometric and physical problems; tensor algebra excels in multilinear mappings and is widely used in continuum mechanics and relativity. Clifford algebra offers a richer geometric structure by integrating vectors, scalars, and multivectors, making it ideal for applications in quantum mechanics, computer graphics, and robotics. Understanding the application's dimensionality and algebraic requirements helps determine whether tensor or Clifford algebra provides the most efficient and expressive mathematical tool.
Tensor algebra Infographic
 libterm.com
libterm.com