A circle is a geometric shape defined by all points equidistant from a central point, known as the radius. Its properties include circumference, diameter, and area, which are essential concepts in both mathematics and everyday applications. Explore this article to deepen your understanding of circles and how they impact your world.
Table of Comparison
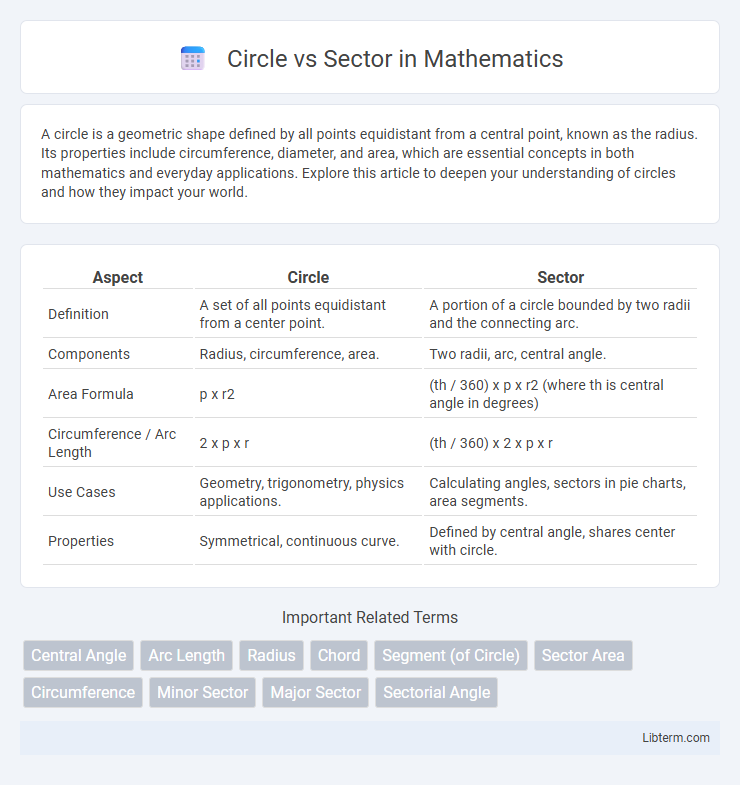
| Aspect | Circle | Sector |
|---|---|---|
| Definition | A set of all points equidistant from a center point. | A portion of a circle bounded by two radii and the connecting arc. |
| Components | Radius, circumference, area. | Two radii, arc, central angle. |
| Area Formula | p x r2 | (th / 360) x p x r2 (where th is central angle in degrees) |
| Circumference / Arc Length | 2 x p x r | (th / 360) x 2 x p x r |
| Use Cases | Geometry, trigonometry, physics applications. | Calculating angles, sectors in pie charts, area segments. |
| Properties | Symmetrical, continuous curve. | Defined by central angle, shares center with circle. |
Understanding Circles: Basic Definition
A circle is a set of all points in a plane equidistant from a fixed center point, defined by its radius. A sector is a portion of a circle enclosed by two radii and the corresponding arc, resembling a "pie slice." Understanding the circle's radius and center helps differentiate sectors as parts of the whole circle, essential in geometry and measurement calculations.
What is a Sector?
A sector is a portion of a circle bounded by two radii and the connecting arc, resembling a slice of pie. It is defined by the central angle between the radii, measured in degrees or radians, which determines the size of the sector relative to the entire circle. The area of a sector can be calculated using the formula (th/360) x pr2 for degrees or (1/2)r2th for radians, where th is the central angle and r is the radius of the circle.
Key Differences Between Circles and Sectors
A circle is a two-dimensional shape defined by all points equidistant from a central point, encompassing the entire area within its circumference. A sector, however, is a portion of a circle bounded by two radii and the connecting arc, representing a specific fraction of the circle's area. Key differences include that a circle is a complete shape with a continuous boundary, while a sector is a segment representing part of the circle, often used to measure angles or proportions within the circle.
Mathematical Formulas: Circle vs Sector
The area of a circle is given by the formula A = pr2, where r represents the radius. For a sector of a circle, the area is calculated using A = (th/360) x pr2, with th denoting the central angle in degrees. The length of the sector's arc is found by L = (th/360) x 2pr, distinguishing sector measurements from the full circle.
Real-Life Applications of Circles
Circles are fundamental in engineering and design, shaping everything from wheels to gears, ensuring smooth rotation and efficient movement. Sectors play a crucial role in fields like navigation and astronomy, where they represent angular portions of circular regions for precise calculations and targeting. Urban planners use circular zones and sectors to model regions of influence, optimize traffic flow, and design efficient public spaces.
Practical Uses of Sectors
Sectors are widely used in various practical applications such as calculating the area of a pizza slice or designing pie charts to represent data visually. Engineers rely on sectors in circular gears to determine torque and stress distribution. In navigation, sectors of circles help define radar and sonar coverage areas for better tracking and detection.
Visual Representation: Circle and Sector Diagrams
Circle diagrams represent a complete 360-degree shape defined by a circumference representing all points equidistant from a center. Sector diagrams depict a portion of a circle, resembling a "slice," bounded by two radii and the arc between them, illustrating a specific fractional part of the whole. Visual representation of sectors emphasizes area proportionality corresponding to data segments, making them essential for pie charts and similar data visualization tools.
Area Calculation: Circle vs Sector
The area of a circle is calculated using the formula A = pr2, where r represents the radius of the circle. For a sector, the area is determined by the fraction of the circle's angle th over 360 degrees, given by A = (th/360) x pr2. Sector area calculation is crucial in various applications, including geometry, engineering, and design, where partial regions of a circle need to be quantified.
Common Misconceptions
A common misconception about circles and sectors is that they are often used interchangeably, despite sectors being a portion of a circle bounded by two radii and an arc. Many people mistakenly believe the area of a sector can be calculated using the same formula as a full circle, ignoring the central angle's proportion of 360 degrees. Understanding the distinction is crucial for accurate geometric calculations and applications such as pie charts and circular segments.
Summary: Circle vs Sector Comparison
A circle is a closed curve with all points equidistant from the center, representing a complete 360-degree area, while a sector is a portion of a circle defined by two radii and the included arc, highlighting a specific segment of the circle. The area of a circle is calculated as pr2, whereas the area of a sector is a fraction of the circle's area, determined by (th/360) x pr2, where th is the central angle in degrees. Circles serve as the basis for various geometric and real-world applications, while sectors are crucial for measuring and analyzing parts of circular shapes, such as pie charts or angle-based divisions.
Circle Infographic
 libterm.com
libterm.com