Analytic sets are a fundamental concept in descriptive set theory, characterized as projections of Borel sets in Polish spaces. These sets possess rich structural properties, playing a crucial role in areas such as measure theory and functional analysis. Discover how understanding analytic sets can deepen your grasp of advanced mathematical frameworks by reading the rest of this article.
Table of Comparison
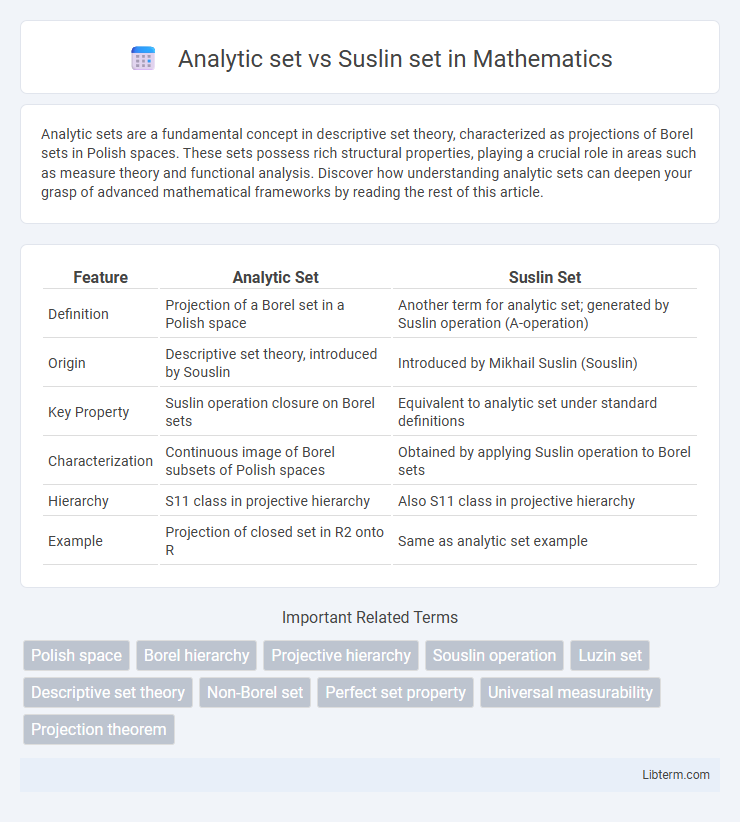
| Feature | Analytic Set | Suslin Set |
|---|---|---|
| Definition | Projection of a Borel set in a Polish space | Another term for analytic set; generated by Suslin operation (A-operation) |
| Origin | Descriptive set theory, introduced by Souslin | Introduced by Mikhail Suslin (Souslin) |
| Key Property | Suslin operation closure on Borel sets | Equivalent to analytic set under standard definitions |
| Characterization | Continuous image of Borel subsets of Polish spaces | Obtained by applying Suslin operation to Borel sets |
| Hierarchy | S11 class in projective hierarchy | Also S11 class in projective hierarchy |
| Example | Projection of closed set in R2 onto R | Same as analytic set example |
Introduction to Analytic Sets
Analytic sets, also known as Suslin sets, are a fundamental class of subsets in descriptive set theory characterized as continuous images of Borel sets in Polish spaces. They extend the concept of Borel sets, providing greater flexibility while retaining definability properties useful in measure theory and topology. The distinction lies in their representation: analytic sets are projections of Borel sets, enabling complex constructions beyond traditional Borel hierarchies.
Definition and Properties of Suslin Sets
Suslin sets, also known as analytic sets, are subsets of Polish spaces that can be constructed as continuous images of Borel sets, making them broader than Borel sets yet still well-structured in descriptive set theory. These sets exhibit closure under countable unions, countable intersections, and continuous images, and every Borel set is a Suslin set, but not all Suslin sets are Borel. The definition emphasizes their characterization via Suslin schemes, linking trees and projections, which highlights their role in complexity hierarchies and measurable selection theorems.
Historical Context: From Suslin Sets to Analytic Sets
Suslin sets originated in the early 20th century through the work of Mikhail Suslin, who identified these sets while studying descriptive set theory and challenging the projective hierarchy's structure. The development of analytic sets emerged as a natural extension, encompassing Suslin sets and providing a broader framework for classifying complex definable sets in Polish spaces. This historical progression marked a pivotal shift from Suslin's original definitions toward a systematic exploration of measurable and topological properties in analytic sets.
Set-Theoretic Foundations: Polish Spaces and Borel Hierarchy
Analytic sets, defined as continuous images of Borel sets in Polish spaces, occupy a crucial position in the projective hierarchy beyond Borel sets yet maintain definability within standard descriptive set theory. Suslin sets, originally introduced by Suslin, coincide with analytic sets and are characterized by their representation via Suslin schemes, emphasizing their constructibility through countable operations on closed sets in Polish spaces. Both classes enrich the Borel hierarchy by illuminating the complexity layers in Polish spaces, providing foundational insight into the interplay between topology, measure, and definability in set theory.
Key Similarities Between Analytic and Suslin Sets
Analytic sets and Suslin sets both arise in descriptive set theory as classes of sets definable from Borel sets using continuous images, leading to their equivalence in Polish spaces. Each set type is closed under continuous images and inverse images of Borel sets, facilitating their role in measurable and topological structure analysis. They share prominent properties such as being universally measurable, possessing the property of Baire, and fitting within the projective hierarchy at the S11 level.
Crucial Differences: Analytic vs. Suslin Sets
Analytic sets, defined as continuous images of Borel sets, are always Suslin sets, but Suslin sets include a broader class that can be generated using Suslin operations on Borel sets. The crucial difference lies in the fact that every analytic set is Suslin, yet not all Suslin sets are analytic, reflecting a subtle hierarchy in descriptive set theory. Analytic sets are projective and possess strong regularity properties, while Suslin sets may lack these properties, highlighting their distinct roles in the classification of complex sets.
Descriptive Set Theory: Role of Analytic and Suslin Sets
Analytic sets, defined as continuous images of Borel sets in Polish spaces, play a critical role in Descriptive Set Theory due to their closure properties under projections and countable operations. Suslin sets coincide with analytic sets in Polish spaces, emphasizing their importance in classifying complex sets beyond Borel hierarchy and facilitating the study of definability and regularity properties. The interplay between analytic and Suslin sets underpins key results in determinacy, measurable selection, and uniformization phenomena within descriptive set frameworks.
Examples Illustrating Analytic and Suslin Sets
Analytic sets, such as the projection of a Borel set in a Polish space, include examples like the set of all irrational numbers formed by projecting the open set of pairs (rational, real) numbers. Suslin sets, also known as A-sets, can be constructed by applying the Suslin operation to a family of closed sets, exemplified by the classical Suslin line which is a non-Borel linear order representing a Suslin set. These examples highlight the subtle differences: analytic sets arise naturally via projections, while Suslin sets are generated through complex countable operations on closed sets.
Applications in Mathematics and Logic
Analytic sets, defined as continuous images of Borel sets in Polish spaces, play a crucial role in descriptive set theory and have applications in real analysis, measure theory, and the classification of definable sets. Suslin sets, synonymous with analytic sets when considered in standard Borel spaces, extend these applications by enabling the construction and study of complex hierarchies within projective sets, impacting the understanding of definability and regularity properties in logic. Both sets facilitate advancements in effective descriptive set theory, model theory, and the analysis of definable functions in mathematics.
Summary and Implications for Further Research
Analytic sets, defined as continuous images of Borel sets, form a well-studied class in descriptive set theory with strong closure properties and effective representation via projection operations. Suslin sets, often synonymous with analytic sets in Polish spaces, highlight nuanced structural characteristics crucial for measure theory and effective descriptive classification. Further research implications involve exploring finer hierarchies within projective sets, enhancing classification algorithms, and investigating connections to determinacy axioms influencing foundational mathematics.
Analytic set Infographic
 libterm.com
libterm.com