A CW complex is a type of topological space constructed by inductively attaching cells of increasing dimension, providing a powerful framework for analyzing complex geometrical structures. This approach simplifies the study of spaces in algebraic topology, enabling efficient computation of homology and cohomology groups. Explore the rest of the article to deepen your understanding of CW complexes and their crucial role in modern topology.
Table of Comparison
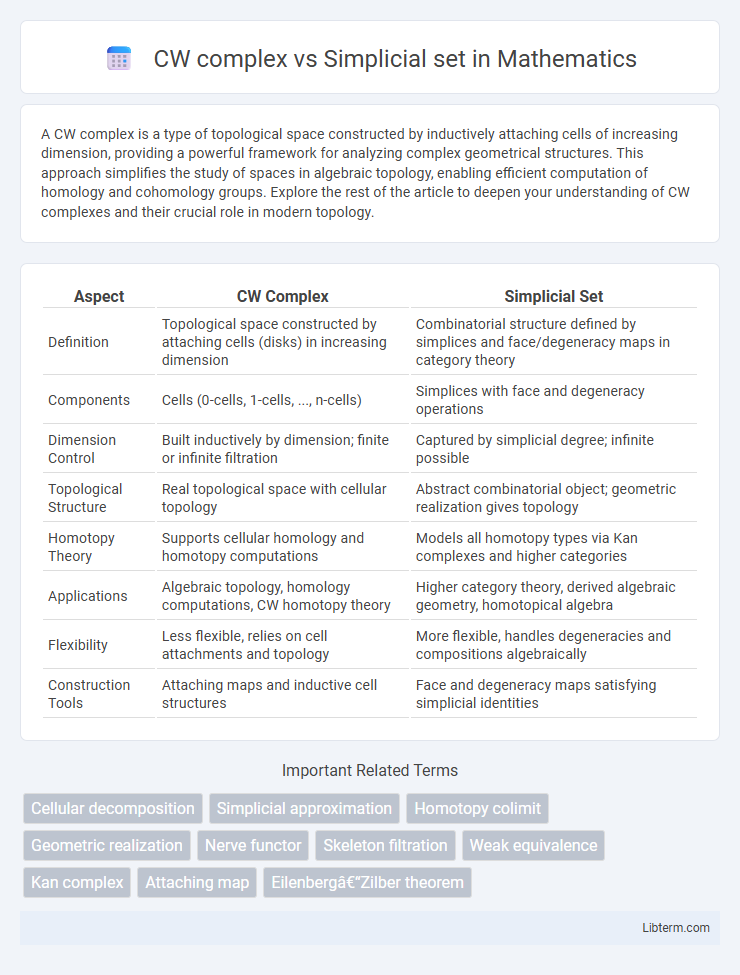
| Aspect | CW Complex | Simplicial Set |
|---|---|---|
| Definition | Topological space constructed by attaching cells (disks) in increasing dimension | Combinatorial structure defined by simplices and face/degeneracy maps in category theory |
| Components | Cells (0-cells, 1-cells, ..., n-cells) | Simplices with face and degeneracy operations |
| Dimension Control | Built inductively by dimension; finite or infinite filtration | Captured by simplicial degree; infinite possible |
| Topological Structure | Real topological space with cellular topology | Abstract combinatorial object; geometric realization gives topology |
| Homotopy Theory | Supports cellular homology and homotopy computations | Models all homotopy types via Kan complexes and higher categories |
| Applications | Algebraic topology, homology computations, CW homotopy theory | Higher category theory, derived algebraic geometry, homotopical algebra |
| Flexibility | Less flexible, relies on cell attachments and topology | More flexible, handles degeneracies and compositions algebraically |
| Construction Tools | Attaching maps and inductive cell structures | Face and degeneracy maps satisfying simplicial identities |
Introduction to CW Complexes and Simplicial Sets
CW complexes provide a geometric framework built from cells glued together inductively, allowing for a flexible topology representation with well-defined homotopy properties. Simplicial sets offer a combinatorial model using simplices and face-degeneracy maps, enabling powerful categorical and algebraic manipulations in homotopy theory. Understanding CW complexes emphasizes their inductive cell structure, whereas simplicial sets focus on abstract simplicial data and higher-dimensional generalizations.
Historical Background and Development
CW complexes emerged in the early 20th century through the work of J.H.C. Whitehead, providing a combinatorial approach to topology by building spaces from cells glued together in increasing dimension. Simplicial sets were developed later in the mid-20th century by Eilenberg and Zilber as an abstraction generalizing simplicial complexes, facilitating homotopical and category-theoretic methods in algebraic topology. Both frameworks advanced the study of topological spaces by enabling computations of homotopy and homology, but simplicial sets offered greater flexibility for higher categorical and homotopical structures.
Formal Definitions: CW Complexes
A CW complex is a topological space constructed by inductively attaching cells of increasing dimension via continuous maps from boundaries of n-dimensional disks to the existing complex. Formally, it consists of a sequence of skeleta X^n where X^0 is a discrete set of points and X^{n} is obtained by attaching n-cells e_{\alpha}^n via characteristic maps ph_{\alpha}: D^n - X^{n}, satisfying the closure-finiteness and weak topology conditions. This inductive process defines the CW complex as a cellular complex with a graded structure tailored to algebraic topology and homotopy theory.
Formal Definitions: Simplicial Sets
A simplicial set is a functor from the simplex category \(\Delta^{op}\) to the category of sets, assigning to each non-negative integer \(n\) a set of \(n\)-simplices equipped with face and degeneracy maps satisfying simplicial identities. Unlike CW complexes, which are topological spaces built inductively using cells attached via attaching maps, simplicial sets provide a combinatorial model for spaces through collections of simplices and their relations. This formal definition enables a higher level of abstraction, facilitating homotopical and categorical analysis in algebraic topology.
Key Differences in Structure and Construction
CW complexes are topological spaces constructed by gluing cells of varying dimensions together via attaching maps, emphasizing a combinatorial cell-by-cell assembly process that facilitates homotopy analysis. Simplicial sets, defined as collections of combinatorial data organized via face and degeneracy maps, provide an algebraic framework capturing homotopy types through simplices and their relationships, allowing for higher categorical and homotopical manipulations. The fundamental structural difference lies in CW complexes' geometric cell attachment versus simplicial sets' purely algebraic simplicial structure, with CW complexes suited for geometric intuition and simplicial sets enabling abstract, functorial homotopy theory.
Comparing Homotopy Theories
CW complexes and simplicial sets both serve as foundational structures in algebraic topology for modeling spaces and their homotopy types. Homotopy theories derived from CW complexes emphasize cellular attachments and characteristic maps, facilitating explicit geometric constructions, while simplicial sets provide combinatorial models equipped with Kan fibrations and horn-filling conditions that enable a flexible and algebraic approach to homotopy theory. Model categories structured on simplicial sets yield a robust framework for higher homotopy operations, often simplifying homotopy limits and colimits compared to the more geometric perspective intrinsic to CW complexes.
Applications in Algebraic Topology
CW complexes provide a versatile framework for studying topological spaces through a cellular decomposition that facilitates computations of homotopy and homology groups. Simplicial sets offer a combinatorial approach that captures higher homotopical structures, enabling the use of model category theory and simplicial homotopy theory in algebraic topology. Both structures support applications such as spectral sequences, homotopy colimits, and the construction of classifying spaces, with simplicial sets allowing more flexible manipulation of infinity-groupoids and derived functors.
Advantages and Limitations of Each Approach
CW complexes provide a flexible, geometric framework ideal for constructing spaces through iterative cell attachments, allowing straightforward computation of homotopy and homology groups, but they may lack the combinatorial precision found in simplicial methods. Simplicial sets offer a highly combinatorial and algebraic approach, facilitating effective use in homotopy theory and higher category theory with strict control over simplices and face maps, yet their geometric intuition can be less direct and constructions more complex. The choice between CW complexes and simplicial sets depends on the balance between geometric intuition and algebraic manipulability required for the topological problem at hand.
Translating Between CW Complexes and Simplicial Sets
Translating between CW complexes and simplicial sets involves constructing simplicial sets that reflect the cellular structure of a CW complex through its attaching maps and cells, preserving homotopy types. The geometric realization functor converts simplicial sets into topological spaces resembling CW complexes, while CW complexes can be decomposed into simplicial sets via singular complexes or simplicial approximations. This translation facilitates algebraic topology computations by enabling the use of combinatorial methods from simplicial sets to analyze cellular structures and vice versa.
Conclusion: Choosing the Right Framework
CW complexes offer a topological framework with intuitive geometric construction and are ideal for studying homotopy types and practical computations in algebraic topology. Simplicial sets provide a combinatorial and algebraic model better suited for higher category theory and homotopical algebra, enabling effective manipulation of complex homotopy-theoretic structures. Selecting between CW complexes and simplicial sets depends on the specific application domain, desired computational approach, and the level of algebraic abstraction required.
CW complex Infographic
 libterm.com
libterm.com