Algebraic functions include polynomials and roots, defined by polynomial equations with coefficients. Analytic functions are characterized by their expressibility as convergent power series, allowing detailed local analysis. Understanding these categories helps deepen your grasp of mathematical functions--explore the rest of the article for a comprehensive breakdown.
Table of Comparison
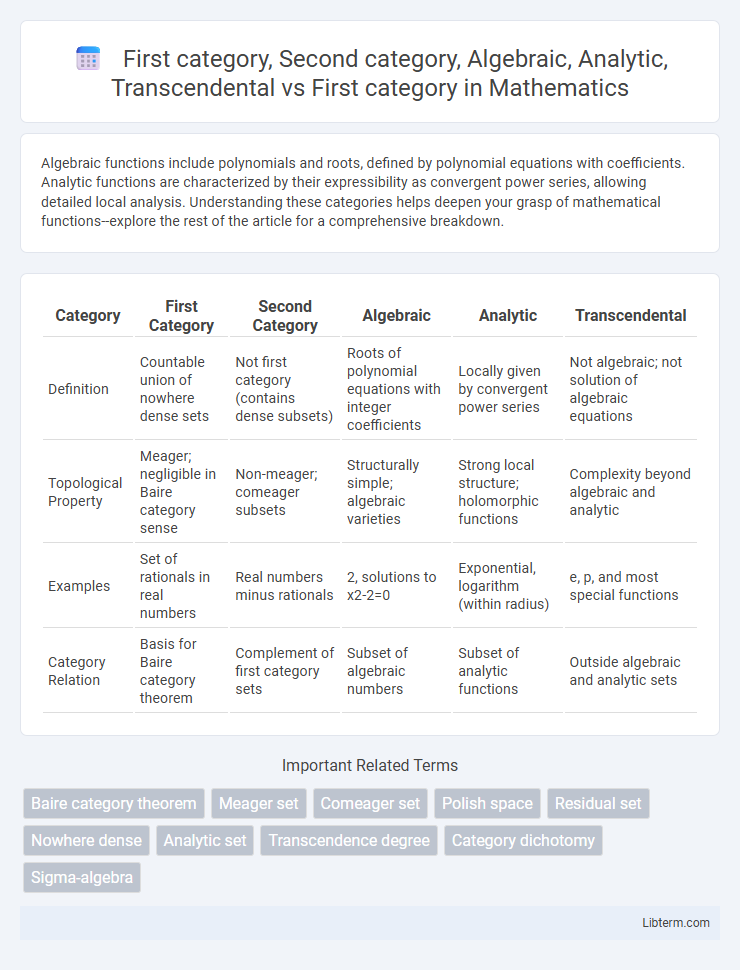
| Category | First Category | Second Category | Algebraic | Analytic | Transcendental |
|---|---|---|---|---|---|
| Definition | Countable union of nowhere dense sets | Not first category (contains dense subsets) | Roots of polynomial equations with integer coefficients | Locally given by convergent power series | Not algebraic; not solution of algebraic equations |
| Topological Property | Meager; negligible in Baire category sense | Non-meager; comeager subsets | Structurally simple; algebraic varieties | Strong local structure; holomorphic functions | Complexity beyond algebraic and analytic |
| Examples | Set of rationals in real numbers | Real numbers minus rationals | 2, solutions to x2-2=0 | Exponential, logarithm (within radius) | e, p, and most special functions |
| Category Relation | Basis for Baire category theorem | Complement of first category sets | Subset of algebraic numbers | Subset of analytic functions | Outside algebraic and analytic sets |
Introduction to Mathematical Categories
First and second category sets classify subsets in topology and measure theory, with first category sets being "small" or meager and second category sets being "large" or non-meager. Algebraic, analytic, and transcendental categories relate to the complexity and definability of sets or functions, where algebraic sets are defined by polynomial equations, analytic sets involve solutions to analytic conditions, and transcendental sets extend beyond algebraic descriptions. Understanding these categories in Introduction to Mathematical Categories provides foundational insight into set classification, measure, and hierarchy in advanced mathematics.
Defining the First Category
The First category, also known as meager sets in topology, comprises subsets of a space that can be expressed as a countable union of nowhere dense sets. In contrast, the Second category includes sets that are not of the First category, often containing "large" or "dense" elements in a topological sense. Algebraic, Analytic, and Transcendental sets differ fundamentally by their definitional structures, with algebraic sets defined by polynomial equations, analytic sets described by convergent power series, and transcendental sets extending beyond algebraic constraints, yet the First category primarily emphasizes topological size and structure rather than algebraic or analytic properties.
Exploring the Second Category
The distinction between first and second category sets is fundamental in topology and analysis, where first category sets are countable unions of nowhere dense sets, making them "small" or meager, while second category sets are not, indicating "larger" or more substantial structure. Algebraic, analytic, and transcendental functions often interact differently with these categories; for instance, algebraic sets may exhibit first category properties in complex spaces, whereas transcendental functions frequently map onto second category sets. Exploring the second category reveals rich topological behaviors and dense subsets critical for understanding function spaces and continuity in real and complex analysis.
Algebraic Sets within First and Second Categories
Algebraic sets, defined as the zero loci of polynomial equations, predominantly belong to the first category in the Baire category framework, indicating they are "small" or meager within the ambient topological space. In contrast, transcendental sets, often associated with analytic or transcendental functions, frequently correspond to the second category, reflecting their "largeness" or residual nature in topology. The distinction between first and second category illuminates the structural complexity of algebraic sets, emphasizing their thinness compared to the more substantial and dense transcendental subsets.
Analytic Sets in Category Theory
First category sets, also known as meager sets, play a fundamental role in descriptive set theory and topology, contrasting with the robust structure of analytic sets, which are continuous images of Polish spaces and are central in category theory due to their definable nature and closure properties. Analytic sets form a significant class within the projective hierarchy, characterized by their stability under continuous mappings and countable operations, facilitating a deep interplay between algebraic and topological structures. Transcendental distinctions arise when comparing algebraic sets, defined by polynomial equations, to analytic and transcendental sets, whereby analytic sets bridge the gap through definability and complexity, crucial for understanding morphisms and fibrations in categorical frameworks.
Transcendental Sets: Concepts and Distinctions
Transcendental sets distinguish themselves from first and second category sets by their lack of algebraic structure and failure to be classified as analytic, embodying properties that resist representation through countable unions or intersections of simpler algebraic or measurable subsets. Unlike algebraic sets defined by polynomial equations, transcendental sets encompass elements such as transcendental numbers, which cannot satisfy any polynomial equation with rational coefficients, highlighting deep complexities in classification within real analysis and descriptive set theory. These distinctions emphasize the unique position of transcendental sets within the hierarchy of definable sets, where their topological and measure-theoretic characteristics diverge substantially from those of first and second category sets traditionally studied in Baire category theory.
First Category vs Second Category: Key Differences
First category sets, also known as meager sets, consist of countable unions of nowhere dense subsets in a topological space, whereas second category sets are their complements, exhibiting more substantial topological presence. Algebraic and analytic sets often fall into the first category due to their intricate local structures, while transcendental sets typically belong to the second category, reflecting higher complexity and density. The key differences hinge on density, structural properties, and the classification within Baire spaces, influencing their roles in analysis and topology.
Algebraic vs Analytic in the First Category Context
In the context of the First category, algebraic functions are defined by polynomial equations with coefficients in a given field, whereas analytic functions possess convergent power series expansions within a radius of convergence, exhibiting differentiability in complex domains. The distinction emphasizes that while all algebraic functions are analytic near points where they are defined, not all analytic functions are algebraic, highlighting transcendental behaviors within the First category framework. This differentiation is critical in complex analysis and algebraic geometry, where the interplay between algebraic constraints and analytic properties determines function classification and behavior.
Transcendental vs First Category: Semantic Implications
First category sets in topology are defined as countable unions of nowhere dense sets, while transcendental numbers transcend algebraic definitions by not being roots of any non-zero polynomial with rational coefficients. The semantic implications of contrasting transcendental numbers with first category sets highlight distinctions between measure and category concepts in mathematical analysis. This comparison underscores the nuanced interplay between algebraic characterization and topological sparsity within the framework of real number classification.
Comparative Analysis and Applications
First category and second category functions differ significantly in classification based on their growth and complexity, with algebraic, analytic, and transcendental functions illustrating these differences through polynomial, convergent power series, and non-algebraic forms respectively. Comparative analysis highlights algebraic functions as solutions to polynomial equations, analytic functions as expressible by convergent power series, and transcendental functions as non-algebraic entities, each applicable in diverse fields such as engineering, physics, and number theory. Applications of first and second category distinctions guide problem-solving approaches, with algebraic and analytic functions suited for exact computation, while transcendental functions model complex phenomena like exponential growth and wave behavior.
First category, Second category, Algebraic, Analytic, Transcendental Infographic
 libterm.com
libterm.com