Fiber bundles are essential components in telecommunications and data transmission, enabling high-speed and reliable connectivity through strands of glass or plastic fibers. These bundles support vast bandwidth capabilities, making them ideal for internet infrastructure and digital communication systems. Explore the following article to understand how fiber bundles can enhance your network performance and future-proof your technology setup.
Table of Comparison
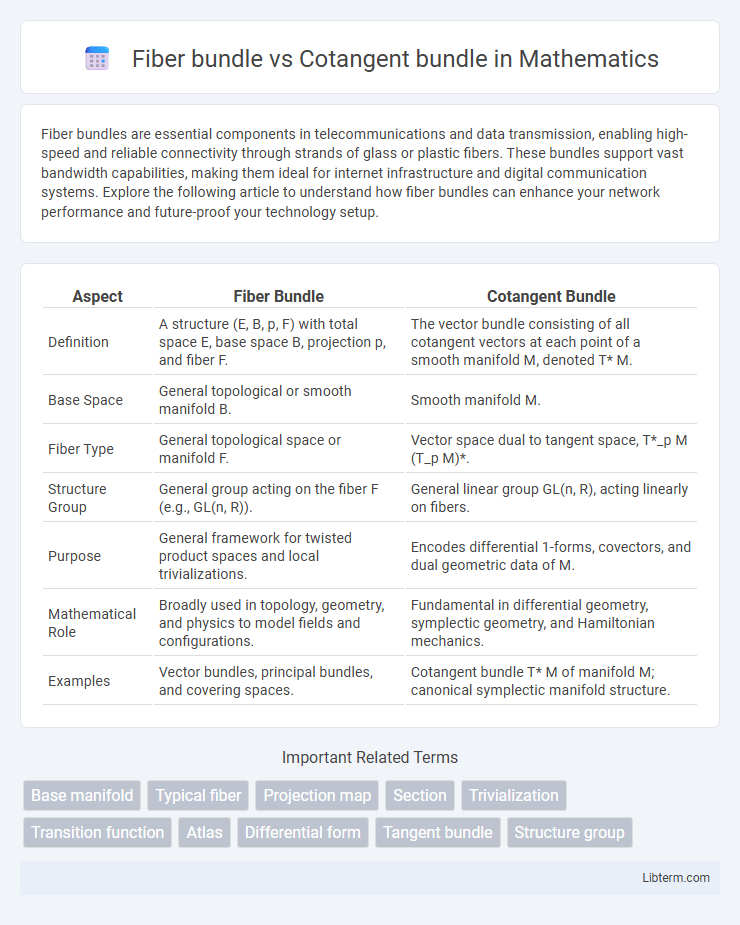
| Aspect | Fiber Bundle | Cotangent Bundle |
|---|---|---|
| Definition | A structure (E, B, p, F) with total space E, base space B, projection p, and fiber F. | The vector bundle consisting of all cotangent vectors at each point of a smooth manifold M, denoted T* M. |
| Base Space | General topological or smooth manifold B. | Smooth manifold M. |
| Fiber Type | General topological space or manifold F. | Vector space dual to tangent space, T*_p M (T_p M)*. |
| Structure Group | General group acting on the fiber F (e.g., GL(n, R)). | General linear group GL(n, R), acting linearly on fibers. |
| Purpose | General framework for twisted product spaces and local trivializations. | Encodes differential 1-forms, covectors, and dual geometric data of M. |
| Mathematical Role | Broadly used in topology, geometry, and physics to model fields and configurations. | Fundamental in differential geometry, symplectic geometry, and Hamiltonian mechanics. |
| Examples | Vector bundles, principal bundles, and covering spaces. | Cotangent bundle T* M of manifold M; canonical symplectic manifold structure. |
Introduction to Fiber Bundles and Cotangent Bundles
Fiber bundles are geometric structures consisting of a base space, a typical fiber, and a projection map that locally resemble a product space, enabling the systematic study of spaces parameterized by manifolds. Cotangent bundles are specific examples of fiber bundles where the fiber at each point of a differentiable manifold is the dual space to the tangent space, consisting of all covectors. These structures play a crucial role in differential geometry and mathematical physics, particularly in the formulation of Hamiltonian mechanics and symplectic geometry.
Defining Fiber Bundles in Differential Geometry
A fiber bundle in differential geometry is a structure consisting of a total space \(E\), a base space \(B\), and a continuous surjective projection map \(\pi: E \to B\) such that the preimage \(\pi^{-1}(b)\) over each point \(b \in B\) is homeomorphic to a typical fiber \(F\). The cotangent bundle \(T^*M\) of a smooth manifold \(M\) is a specific example of a fiber bundle where the fiber over each point is the dual space to the tangent space, \(T^*_p M\), consisting of covectors at \(p\). Fiber bundles generalize this concept by allowing arbitrary fibers and structure groups, enabling the study of geometric and topological properties in a unified framework.
The Structure of Cotangent Bundles
The cotangent bundle \( T^*M \) of a smooth manifold \( M \) is a specific example of a fiber bundle where each fiber is the dual space of the tangent space at a point, consisting of covectors. Its structure is inherently symplectic, equipped with the canonical symplectic form arising from the exterior derivative of the Liouville 1-form, distinguishing it from general fiber bundles. This symplectic structure plays a crucial role in Hamiltonian mechanics and geometric quantization, making the cotangent bundle a central object in differential geometry and mathematical physics.
Key Differences Between Fiber Bundles and Cotangent Bundles
Fiber bundles consist of a base space and a typical fiber, allowing different types of fibers, such as vector spaces or manifolds, while cotangent bundles specifically bundle together cotangent spaces of a manifold, forming a vector bundle whose fibers are dual spaces to tangent spaces. Fiber bundles generalize structures like vector bundles and principal bundles, whereas cotangent bundles carry a canonical symplectic structure critical in differential geometry and Hamiltonian mechanics. The cotangent bundle T* M of a manifold M serves as the phase space in classical mechanics, contrasting with more general fiber bundles which may lack intrinsic geometric structures.
Fiber Bundle Examples and Applications
Fiber bundles generalize the concept of a product space by allowing a "fiber" space to vary smoothly across a "base" space, with examples including vector bundles and principal bundles essential in gauge theory and differential geometry. The cotangent bundle, a specific fiber bundle whose fibers are the cotangent spaces at each point of a manifold, plays a critical role in classical mechanics and symplectic geometry by enabling the formulation of phase space for Hamiltonian dynamics. Applications of fiber bundles extend to formulating gauge fields in physics, studying characteristic classes in topology, and modeling complex spaces in string theory, where the cotangent bundle provides the geometric framework for momentum and differential forms.
Geometric Importance of Cotangent Bundles
Cotangent bundles play a crucial role in differential geometry by providing a natural setting for differential forms and symplectic structures, which are fundamental in Hamiltonian mechanics and symplectic geometry. Unlike general fiber bundles that can have arbitrary fibers, cotangent bundles specifically pair each point of a manifold with its dual tangent space, facilitating the study of duality and canonical transformations. This intrinsic geometric construction enables powerful tools for analyzing phase spaces, variational principles, and conserved quantities in mathematical physics.
Mathematical Formulation: Fiber Bundles vs Cotangent Bundles
Fiber bundles consist of a total space \(E\), a base space \(B\), and a projection map \(\pi: E \to B\) where each fiber \( \pi^{-1}(b) \) is homeomorphic to a typical fiber \(F\), allowing local trivializations \(U \times F \cong \pi^{-1}(U)\) over open sets \(U \subseteq B\). Cotangent bundles are a special case of fiber bundles where the fibers are the dual spaces of tangent spaces, defined as \(T^*M = \bigsqcup_{x \in M} T_x^*M\) with a smooth structure inherited from the manifold \(M\), and projection \(\pi: T^*M \to M\). The cotangent bundle \(T^*M\) carries a natural symplectic structure and canonical 1-form, distinguishing it within the broader category of fiber bundles used in differential geometry.
Role in Modern Physics and Geometry
The fiber bundle provides a general framework for describing spaces that locally resemble a product of two spaces, essential in gauge theories and general relativity for modeling fields and spacetime structures. The cotangent bundle, as a specific fiber bundle consisting of all cotangent spaces of a manifold, plays a crucial role in symplectic geometry and classical mechanics by encoding phase space variables and facilitating Hamiltonian dynamics. Both structures underpin the geometric formulation of modern physics, with fiber bundles handling the global topological aspects and cotangent bundles focusing on local differential and symplectic properties.
Advantages and Limitations of Each Bundle Type
Fiber bundles provide a versatile framework for modeling smoothly varying spaces parameterized by a base manifold, with advantages including flexibility in choosing typical fibers and wide applicability in areas such as gauge theory and topology. Cotangent bundles specifically encode the geometric structure of phase space in classical mechanics, offering natural symplectic forms crucial for Hamiltonian dynamics and providing canonical coordinates for differential forms. Limitations of fiber bundles arise from potential complexity in trivialization and structural group selection, while cotangent bundles are constrained to dual tangent spaces, limiting their direct applicability outside smooth manifold structures and symplectic geometry contexts.
Conclusion: Choosing Between Fiber and Cotangent Bundles
Choosing between fiber bundles and cotangent bundles depends on the geometric and analytical context; fiber bundles provide a broad framework for modeling various types of fibers over manifolds, while cotangent bundles specifically encode differential properties related to covectors and symplectic geometry. For applications involving differentiation, Hamiltonian mechanics, or phase space analysis, cotangent bundles offer a natural and structurally rich setting. Fiber bundles are preferred for more general topological or geometric constructions where the nature of the fiber varies widely beyond just cotangent spaces.
Fiber bundle Infographic
 libterm.com
libterm.com