Euclidean geometry forms the foundation of classical mathematics, focusing on points, lines, and shapes in a flat, two-dimensional plane. Its principles, established by the ancient Greek mathematician Euclid, are essential for understanding spatial relationships and solving practical problems in fields like architecture and engineering. Explore the rest of this article to deepen your knowledge of Euclidean concepts and their real-world applications.
Table of Comparison
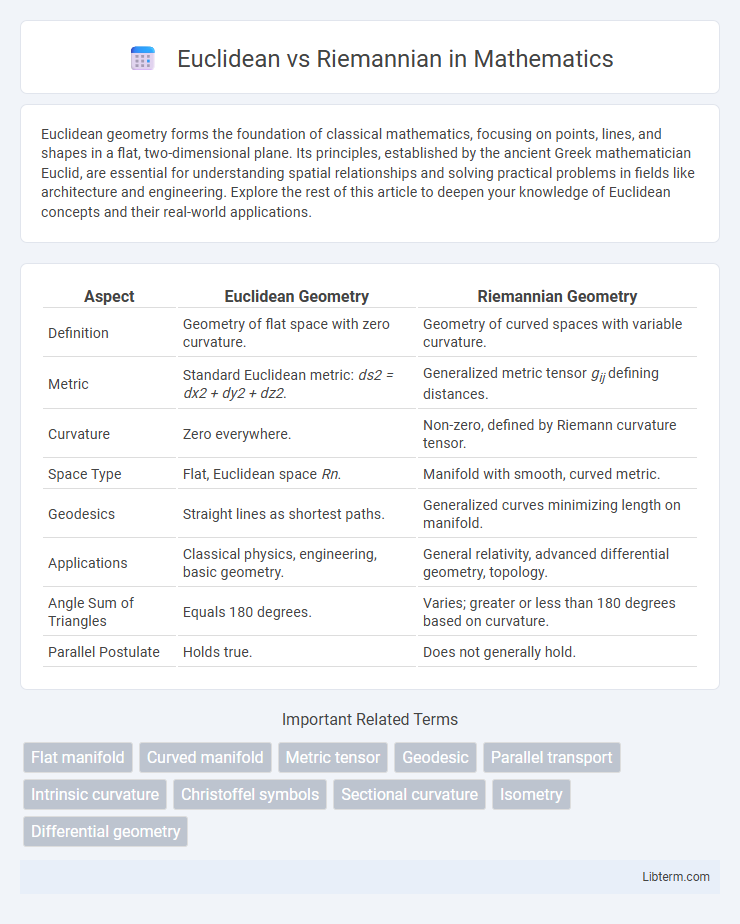
| Aspect | Euclidean Geometry | Riemannian Geometry |
|---|---|---|
| Definition | Geometry of flat space with zero curvature. | Geometry of curved spaces with variable curvature. |
| Metric | Standard Euclidean metric: ds2 = dx2 + dy2 + dz2. | Generalized metric tensor gij defining distances. |
| Curvature | Zero everywhere. | Non-zero, defined by Riemann curvature tensor. |
| Space Type | Flat, Euclidean space Rn. | Manifold with smooth, curved metric. |
| Geodesics | Straight lines as shortest paths. | Generalized curves minimizing length on manifold. |
| Applications | Classical physics, engineering, basic geometry. | General relativity, advanced differential geometry, topology. |
| Angle Sum of Triangles | Equals 180 degrees. | Varies; greater or less than 180 degrees based on curvature. |
| Parallel Postulate | Holds true. | Does not generally hold. |
Introduction to Geometrical Frameworks
Euclidean geometry is based on flat, zero-curvature spaces characterized by familiar concepts such as straight lines and right angles, making it suitable for classical physical modeling. Riemannian geometry generalizes this framework by allowing curved spaces with variable curvature, enabling the study of more complex manifolds like those used in general relativity. Understanding these frameworks is essential for advancing in fields such as differential geometry, mathematical physics, and modern theoretical computer science.
Defining Euclidean Geometry
Euclidean geometry is defined by its foundation on flat, two-dimensional planes and three-dimensional spaces governed by parallel postulates and consistent distance measures based on the Euclidean metric. It relies on axioms established by the ancient Greek mathematician Euclid, where angles, lines, and shapes follow predictable rules such as the sum of angles in a triangle always equaling 180 degrees. This contrasts with Riemannian geometry, which generalizes these concepts to curved surfaces and spaces with variable curvature, using Riemannian metrics to describe distances and angles intricately.
Fundamentals of Riemannian Geometry
Euclidean geometry emphasizes flat spaces characterized by zero curvature, where distances and angles are computed using the standard dot product. Riemannian geometry generalizes these concepts to curved manifolds equipped with a smoothly varying positive-definite metric tensor that defines inner products on tangent spaces. The fundamental objects include the Riemannian metric, geodesics as locally distance-minimizing curves, and curvature tensors measuring intrinsic curvature of the manifold.
Key Differences Between Euclidean and Riemannian Spaces
Euclidean spaces are flat with zero curvature, defined by familiar geometric notions of straight lines and angles, while Riemannian spaces incorporate variable curvature allowing for the study of more complex, curved surfaces. The metric tensor in Euclidean geometry remains constant and simple, but in Riemannian geometry, it varies smoothly, encoding curvature and enabling distance measurements on manifolds. These differences impact applications in physics and differential geometry, where Euclidean geometry models flat space, and Riemannian geometry models curved spacetime and complex shapes.
Metric Concepts: Distance and Curvature
Euclidean geometry defines distance with the familiar metric derived from the Pythagorean theorem, resulting in a flat space where curvature is zero everywhere. In contrast, Riemannian geometry generalizes the concept of distance using a metric tensor that varies smoothly across the manifold, enabling the measurement of distances in curved spaces. Curvature in Riemannian geometry is quantified by objects such as the Riemann curvature tensor, which captures how the manifold bends and differs fundamentally from the zero curvature characteristic of Euclidean spaces.
Role of Parallelism and Geodesics
In Euclidean geometry, parallelism is defined by the existence of straight lines that never intersect, with geodesics corresponding to these straight lines. Riemannian geometry generalizes this concept by defining geodesics as the shortest paths between points on curved manifolds, where parallelism is described through parallel transport along these geodesics. The distinction highlights that Euclidean parallelism is globally consistent, while in Riemannian spaces, parallelism is local and depends on the manifold's curvature.
Applications in Physics and Engineering
Euclidean geometry underpins classical mechanics and engineering design, enabling precise calculations of distances and angles in flat space, essential for structural analysis and robotics. Riemannian geometry extends these principles to curved spaces, playing a crucial role in general relativity by describing gravitational fields and spacetime curvature in astrophysics. In engineering, Riemannian metrics aid in advanced material science and computer vision, where non-Euclidean data structures require sophisticated geometric frameworks for modeling and optimization.
Visualization: Flat versus Curved Spaces
Euclidean geometry visualizes spaces as flat planes with parallel lines that never intersect, enabling straightforward distance and angle measurements using familiar Cartesian coordinates. In contrast, Riemannian geometry deals with curved surfaces where parallel lines may converge or diverge, requiring the use of a metric tensor to accurately represent distances and angles on manifolds. This curvature fundamentally alters visualization, making Riemannian spaces essential for modeling complex shapes like spheres or general relativity's spacetime.
Mathematical Implications in Modern Science
Euclidean geometry, based on flat, two- or three-dimensional space with parallel lines that never intersect, serves as the foundation for classical mechanics and traditional physics problems. Riemannian geometry generalizes these concepts to curved spaces and manifolds, enabling the precise mathematical modeling of gravitational fields in General Relativity and complex data structures in modern theoretical physics. The shift from Euclidean to Riemannian frameworks allows scientists to explore non-Euclidean metrics, curvature tensors, and geodesics, revolutionizing our understanding of space, time, and multidimensional scientific phenomena.
Conclusion: Choosing the Right Geometry
Selecting between Euclidean and Riemannian geometry depends on the context and application; Euclidean geometry suits flat, everyday spaces with consistent distances and angles, while Riemannian geometry is essential for curved spaces such as those encountered in general relativity or complex manifolds. Understanding intrinsic curvature and metric tensors in Riemannian spaces enables accurate modeling of non-Euclidean structures, whereas Euclidean geometry simplifies problems with zero curvature. The right geometric framework enhances precision in disciplines from physics to computer vision by aligning mathematical properties with the spatial characteristics of the problem domain.
Euclidean Infographic
 libterm.com
libterm.com