Urysohn's Lemma establishes a fundamental result in topology, stating that for any two disjoint closed sets in a normal space, there exists a continuous function mapping the whole space to the unit interval [0,1] that separates these sets. This lemma is pivotal in understanding how continuous functions can be constructed to approximate characteristic functions, providing a basis for further analysis in metric spaces. Explore the rest of the article to discover how Urysohn's Lemma applies to your study of topological spaces and their properties.
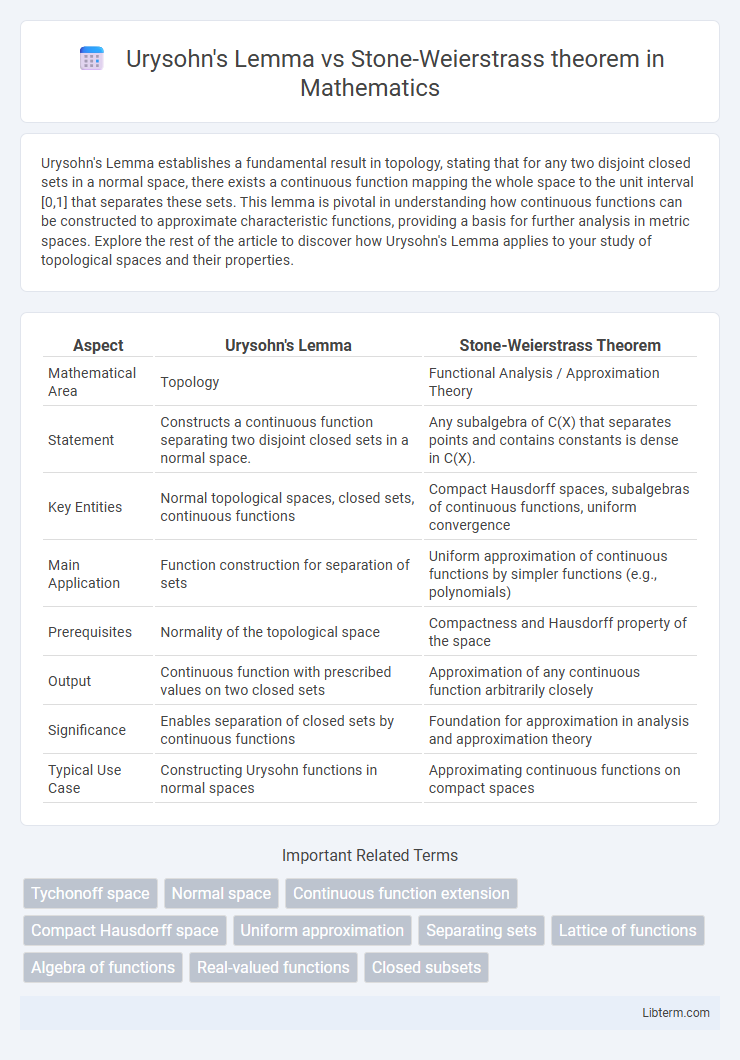
Table of Comparison
| Aspect | Urysohn's Lemma | Stone-Weierstrass Theorem |
|---|---|---|
| Mathematical Area | Topology | Functional Analysis / Approximation Theory |
| Statement | Constructs a continuous function separating two disjoint closed sets in a normal space. | Any subalgebra of C(X) that separates points and contains constants is dense in C(X). |
| Key Entities | Normal topological spaces, closed sets, continuous functions | Compact Hausdorff spaces, subalgebras of continuous functions, uniform convergence |
| Main Application | Function construction for separation of sets | Uniform approximation of continuous functions by simpler functions (e.g., polynomials) |
| Prerequisites | Normality of the topological space | Compactness and Hausdorff property of the space |
| Output | Continuous function with prescribed values on two closed sets | Approximation of any continuous function arbitrarily closely |
| Significance | Enables separation of closed sets by continuous functions | Foundation for approximation in analysis and approximation theory |
| Typical Use Case | Constructing Urysohn functions in normal spaces | Approximating continuous functions on compact spaces |
Introduction to Urysohn's Lemma and Stone-Weierstrass Theorem
Urysohn's Lemma establishes the existence of continuous functions that separate disjoint closed subsets in normal topological spaces, enabling the construction of functions with prescribed values on these sets. The Stone-Weierstrass Theorem generalizes the Weierstrass approximation theorem, asserting that any algebra of continuous functions that separates points and contains the constant functions is dense in the space of all continuous functions on a compact Hausdorff space. Both results play foundational roles in topology and functional analysis by providing tools for approximating and constructing continuous functions with specific properties.
Historical Background and Development
Urysohn's Lemma, developed by Pavel Urysohn in 1925, played a pivotal role in the advancement of topology by providing a bridge between normal spaces and continuous functions. The Stone-Weierstrass theorem, introduced by Marshall Stone in 1937, extended Weierstrass's approximation theorem to a broader class of function algebras, significantly impacting functional analysis. Both results emerged from early 20th-century efforts to understand continuity and approximation, shaping modern analysis and topology.
Formal Statements of Urysohn's Lemma
Urysohn's Lemma states that for any two disjoint closed subsets \(A\) and \(B\) of a normal topological space \(X\), there exists a continuous function \(f: X \to [0,1]\) such that \(f(A) = \{0\}\) and \(f(B) = \{1\}\). This lemma is fundamental in topology for constructing continuous functions that separate closed sets, ensuring the existence of such functions under normality conditions. Unlike the Stone-Weierstrass theorem, which concerns uniform approximation of continuous functions by subalgebras, Urysohn's Lemma provides a constructive method for specific continuous functions with prescribed boundary values.
Formal Statements of Stone-Weierstrass Theorem
The Stone-Weierstrass theorem formally states that any subalgebra of C(X), the algebra of continuous real-valued functions on a compact Hausdorff space X, which separates points and contains the constant functions, is dense in C(X) with respect to the uniform norm. This theorem generalizes the classical Weierstrass approximation theorem by extending polynomial approximations to more abstract function algebras. In contrast, Urysohn's Lemma provides the existence of continuous functions separating closed sets in normal topological spaces, serving as a fundamental tool to prove the separation conditions required in the Stone-Weierstrass theorem.
Topological Foundations: Normality and Compactness
Urysohn's Lemma relies on the normality of a topological space to guarantee the existence of continuous functions that separate closed sets, making it fundamental in the study of normal spaces. The Stone-Weierstrass theorem extends these ideas by requiring the space to be compact Hausdorff for the density of subalgebras of continuous functions, enabling uniform approximation of continuous functions. Normality ensures function separation in Urysohn's Lemma, while compactness and the algebraic structure of functions are crucial for approximation in the Stone-Weierstrass theorem.
Applications of Urysohn's Lemma in Topology
Urysohn's Lemma plays a crucial role in topology by enabling the construction of continuous functions that separate closed sets in normal spaces, thereby facilitating the embedding of such spaces into function spaces. This lemma is foundational for proving the Tietze Extension Theorem and supports the analysis of normal topological spaces through continuous real-valued functions. Unlike the Stone-Weierstrass theorem, which approximates functions uniformly on compact spaces, Urysohn's Lemma provides the essential tool for demonstrating the existence of these separating functions in general normal spaces.
Applications of Stone-Weierstrass Theorem in Analysis
The Stone-Weierstrass theorem enables the approximation of continuous functions on compact spaces by polynomials or other algebraic structures, facilitating the study of function spaces in real and complex analysis. It is instrumental in proving the density of subalgebras in C(X), which underpins spectral theory and the theory of Banach algebras. Applications include approximating solutions to differential equations, constructing functional calculi, and analyzing uniform convergence in spaces of continuous functions.
Comparative Analysis: Key Differences and Similarities
Urysohn's Lemma provides a method to construct continuous functions separating closed sets in normal topological spaces, emphasizing existence and function construction in separation axioms. The Stone-Weierstrass theorem extends the Weierstrass approximation theorem by characterizing dense subalgebras of continuous functions on compact Hausdorff spaces, focusing on uniform approximation of continuous functions by algebraic structures. Both theorems highlight the interplay between topology and continuous functions, but Urysohn addresses function existence for separation, while Stone-Weierstrass centers on approximation and algebraic density properties.
Interconnections and Synergy Between the Theorems
Urysohn's Lemma provides a constructive method to separate closed sets in normal topological spaces by continuous functions, laying the groundwork for the approximation techniques central to the Stone-Weierstrass theorem. The Stone-Weierstrass theorem further extends this framework by characterizing algebras of continuous functions that can uniformly approximate any continuous function on compact spaces, relying on the separation properties guaranteed by Urysohn's Lemma. Together, these theorems synergize to connect topological separation axioms with functional approximation capabilities, enabling deep analysis in functional analysis and topology.
Conclusion: Impact in Modern Mathematical Theory
Urysohn's Lemma establishes the ability to construct continuous functions separating closed sets in normal topological spaces, which is fundamental for embedding these spaces into function spaces. The Stone-Weierstrass theorem generalizes the classical Weierstrass approximation theorem, enabling uniform approximation of continuous functions by algebraic subalgebras, thereby advancing functional analysis and approximation theory. Together, these results play a critical role in modern mathematical theory by linking topology, functional analysis, and algebraic structures, facilitating developments in areas such as C*-algebras and spectral theory.
Urysohn's Lemma Infographic
 libterm.com
libterm.com