Product topology is the topology on a product of topological spaces where the open sets are generated by the Cartesian product of open sets from each factor space. This construction preserves continuity of projection maps and is fundamental in understanding convergence, compactness, and connectedness in product spaces. Explore further to see how product topology plays a crucial role in modern topology and its applications.
Table of Comparison
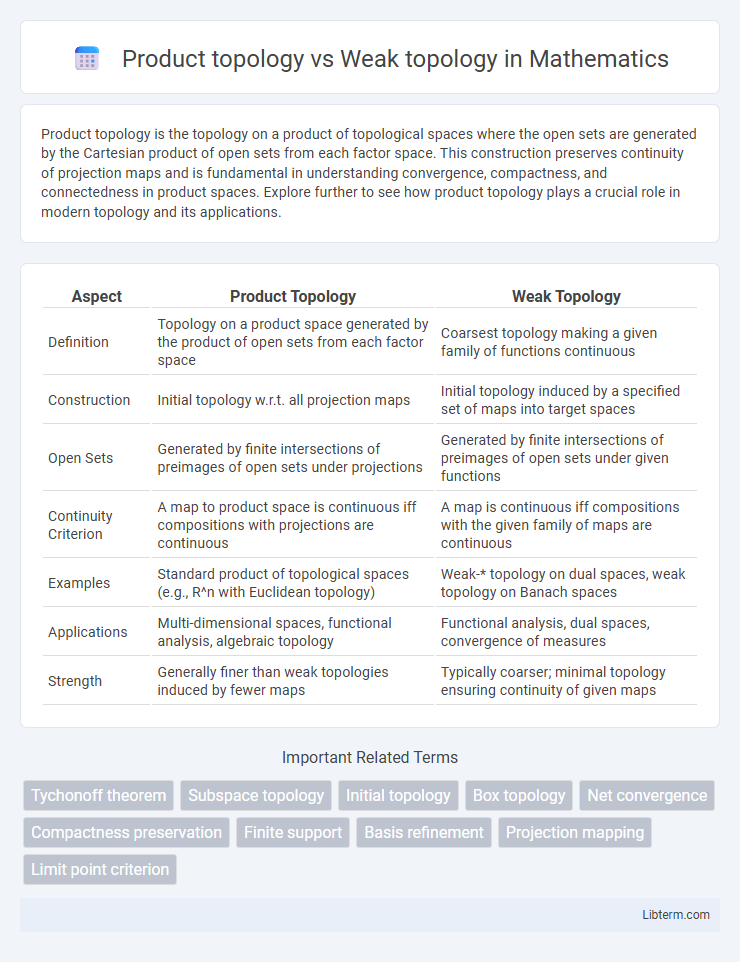
| Aspect | Product Topology | Weak Topology |
|---|---|---|
| Definition | Topology on a product space generated by the product of open sets from each factor space | Coarsest topology making a given family of functions continuous |
| Construction | Initial topology w.r.t. all projection maps | Initial topology induced by a specified set of maps into target spaces |
| Open Sets | Generated by finite intersections of preimages of open sets under projections | Generated by finite intersections of preimages of open sets under given functions |
| Continuity Criterion | A map to product space is continuous iff compositions with projections are continuous | A map is continuous iff compositions with the given family of maps are continuous |
| Examples | Standard product of topological spaces (e.g., R^n with Euclidean topology) | Weak-* topology on dual spaces, weak topology on Banach spaces |
| Applications | Multi-dimensional spaces, functional analysis, algebraic topology | Functional analysis, dual spaces, convergence of measures |
| Strength | Generally finer than weak topologies induced by fewer maps | Typically coarser; minimal topology ensuring continuity of given maps |
Introduction to Product and Weak Topologies
Product topology on a set arises from the Cartesian product of topological spaces, where the open sets are generated by the product of open sets in each factor space, ensuring continuity of projection maps. Weak topology, also called initial topology, is defined by the coarsest topology making a given family of functions continuous, often used to embed complex spaces into simpler ones. Both topologies facilitate analysis in functional analysis and topology by structuring spaces through either coordinate-wise openness (product) or function-induced continuity constraints (weak).
Fundamental Concepts in Topological Spaces
Product topology is formed by the Cartesian product of topological spaces, where the basis consists of products of open sets from each factor space, providing the coarsest topology making all projection maps continuous. Weak topology, also called initial topology, is defined relative to a family of functions from a set into topological spaces, generating the coarsest topology that makes all these functions continuous. Both topologies emphasize continuity and openness, with product topology focusing on coordinate-wise structure while weak topology depends on continuity of mapped functions.
Defining the Product Topology
The product topology on a Cartesian product of topological spaces is defined as the coarsest topology making all projection maps continuous, generated by the basis consisting of all products of open sets where only finitely many factors differ from the entire space. In contrast, the weak topology on a set induced by a family of functions is the coarsest topology making all those functions continuous, generally defined by sub-basis elements formed by inverse images of open sets in the codomain. The product topology emphasizes continuity of projections and opens in each coordinate, ensuring convergence and topological properties are preserved component-wise.
Understanding the Weak Topology
The weak topology on a set X induced by a family of functions {f_i} into topological spaces is the coarsest topology making all f_i continuous, contrasting with the product topology which is the standard topology on the Cartesian product of spaces. Understanding the weak topology involves analyzing how convergence and continuity are determined solely by the convergence of images under the functions f_i, often simplifying complex structures by reducing to pointwise behavior. This approach is essential in functional analysis and optimization, where weak topologies facilitate compactness and continuity arguments that the product topology may not support.
Key Differences Between Product and Weak Topologies
The product topology on a Cartesian product of topological spaces is generated by the basis consisting of all products of open sets from the factor spaces, ensuring that projections are continuous and the topology is the coarsest with this property. The weak topology, often defined via a family of maps into a topological space, is characterized as the coarsest topology making these maps continuous, typically resulting in fewer open sets than the product topology unless the family of maps is the full set of projections. Key differences include the product topology's construction directly from open sets in each component space versus the weak topology's dependence on arbitrary maps, influencing continuity and convergence in functional analysis and infinite-dimensional topology.
Basic Properties of Product Topology
Product topology is defined as the coarsest topology making all projection maps continuous from the product of topological spaces, ensuring each factor's open sets correspond to cylinder sets in the product. Its basis consists of finite intersections of open sets from the component spaces through projections, which guarantees Tychonoff's theorem and preservation of compactness under arbitrary products. Unlike weak topology, product topology has a universal property with respect to continuous maps into the product space, making it fundamental in analysis and topology.
Basic Properties of Weak Topology
Weak topology on a set X induced by a family of maps {f_i: X - Y_i} is the coarsest topology making all f_i continuous, contrasting with the product topology which is generated by the product of topologies from each Y_i. Basic properties of weak topology include initiality, meaning it is the initial topology with respect to the family {f_i}, ensuring continuity of any function g: Z - X if and only if all compositions f_i g are continuous. The weak topology is generally coarser than the product topology, leading to fewer open sets and often simpler convergence criteria.
Applications and Examples of Product and Weak Topologies
Product topology enables the study of spaces constructed from arbitrary Cartesian products of topological spaces, commonly applied in functional analysis and infinite-dimensional vector spaces to analyze convergence and continuity properties. Weak topology, often employed in Banach spaces and Hilbert spaces, provides a framework for examining convergence with respect to dual space functionals, crucial in optimization and variational problems. Examples include the product topology on infinite-dimensional cube spaces facilitating Tychonoff's theorem applications, and the weak topology on Lp spaces guiding compactness and convergence in measure theory.
Advantages and Limitations of Each Topology
Product topology enables the construction of a topological space that preserves continuity for all projections, making it ideal for handling infinite-dimensional spaces and ensuring that a function is continuous if and only if all its component functions are continuous. Its main limitation is the often complex and large basis, which can lead to challenges in practical computations and analysis. Weak topology, generated by a family of functions typically from a dual space, offers a coarser topology that simplifies convergence analysis and compactness arguments but lacks the finer separation properties found in product topologies, sometimes resulting in less intuitive geometric interpretations.
Conclusion: Choosing Between Product and Weak Topologies
Choosing between product topology and weak topology depends on the specific convergence and continuity requirements of a function space or a topological product. Product topology ensures convergence and continuity componentwise, making it suitable for analyzing multidimensional spaces with independent coordinate behavior. Weak topology, often defined by a family of functions or linear functionals, is preferred when minimal topology is desired for weak convergence, such as in functional analysis or when dealing with dual spaces.
Product topology Infographic
 libterm.com
libterm.com