The torsion submodule of a module consists of all elements annihilated by some nonzero scalar from the ring, revealing important structural properties about the module's behavior under scalar multiplication. Understanding this submodule helps in analyzing modules over integral domains, where torsion elements indicate dependencies affecting module decompositions. Explore the rest of the article to deepen your grasp of torsion submodules and their role in module theory.
Table of Comparison
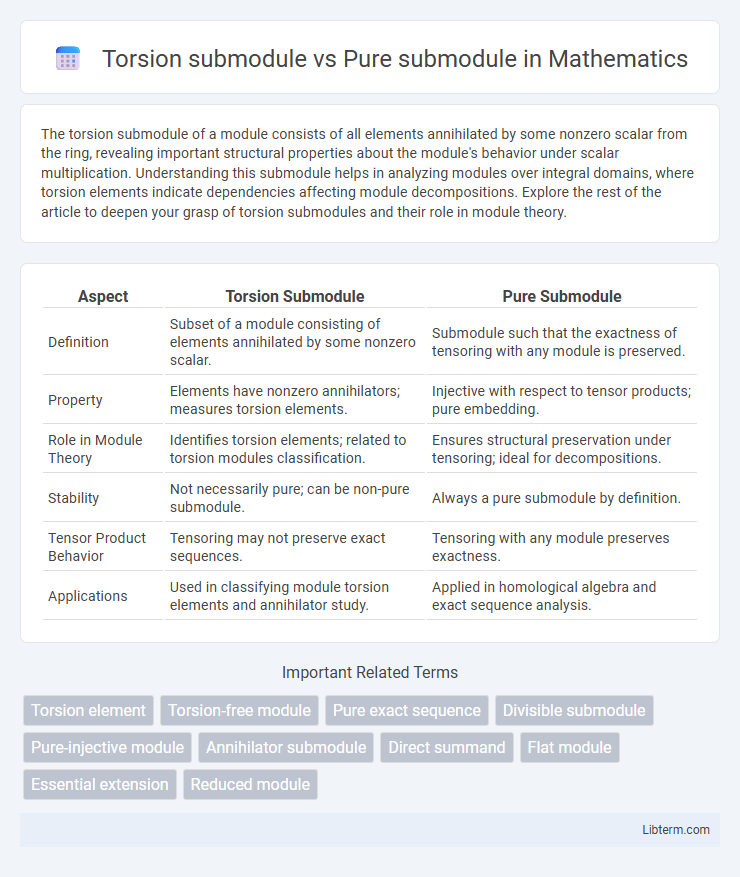
| Aspect | Torsion Submodule | Pure Submodule |
|---|---|---|
| Definition | Subset of a module consisting of elements annihilated by some nonzero scalar. | Submodule such that the exactness of tensoring with any module is preserved. |
| Property | Elements have nonzero annihilators; measures torsion elements. | Injective with respect to tensor products; pure embedding. |
| Role in Module Theory | Identifies torsion elements; related to torsion modules classification. | Ensures structural preservation under tensoring; ideal for decompositions. |
| Stability | Not necessarily pure; can be non-pure submodule. | Always a pure submodule by definition. |
| Tensor Product Behavior | Tensoring may not preserve exact sequences. | Tensoring with any module preserves exactness. |
| Applications | Used in classifying module torsion elements and annihilator study. | Applied in homological algebra and exact sequence analysis. |
Introduction to Modules in Algebra
A torsion submodule of a module M over a ring R consists of elements annihilated by nonzero elements of R, capturing the module's elements with finite order under multiplication. In contrast, a pure submodule N of M retains exact sequences upon tensoring with any R-module, reflecting a structural compatibility stronger than mere submodule inclusion. Understanding the distinction between torsion submodules, which generalize torsion elements in abelian groups, and pure submodules is fundamental in the study of module theory and homological algebra.
Defining Torsion Submodules
A torsion submodule of an R-module M consists of all elements annihilated by some nonzero element of the ring R, capturing those elements with torsion behavior relative to R. Pure submodules, by contrast, are submodules N of M for which the embedding N - M preserves all solution sets of linear equations over R, ensuring exact sequences remain pure. Defining torsion submodules involves identifying elements x in M such that there exists a nonzero r in R with r*x = 0, highlighting the fundamental nature of torsion in module theory.
Understanding Pure Submodules
A pure submodule N of a module M over a ring R is characterized by the property that the tensor product with any R-module preserves exact sequences, ensuring that the inclusion map N - M remains exact after tensoring. Unlike torsion submodules, which consist of elements annihilated by regular elements of R, pure submodules reflect structural compatibility with M and maintain solvability of linear equations within N as they do in M. Understanding pure submodules is crucial for module theory and homological algebra because they facilitate decompositions and retain essential properties under base change and extension operations.
Key Differences Between Torsion and Pure Submodules
Torsion submodules consist of elements annihilated by some nonzero scalar, highlighting a restriction on module elements tied to torsion elements, while pure submodules maintain exactness in tensoring, preserving solution sets across module extensions. Torsion submodules are generally related to modules over integral domains, capturing elements with finite order, whereas pure submodules ensure that embeddings remain exact under any tensor product, reflecting a structural purity in the module category. The key difference lies in torsion submodules focusing on annihilation properties, while pure submodules emphasize preservation of module-theoretic and homological properties through purity conditions.
Examples Illustrating Torsion Submodules
Torsion submodules consist of elements annihilated by nonzero elements of the ring, such as the torsion subgroup of the abelian group \(\mathbb{Z}/n\mathbb{Z}\), where every element is torsion of order dividing \(n\). A classical example is the torsion submodule of \(\mathbb{Q}/\mathbb{Z}\), containing all elements of finite order, representing a divisible torsion group. By contrast, pure submodules preserve tensor exactness, exemplified by the submodule \(\mathbb{Z}\) inside \(\mathbb{Q}\), which is pure but torsion-free, highlighting the fundamental difference in structure and behavior between torsion and pure submodules.
Examples Demonstrating Pure Submodules
A pure submodule of a module \( M \) over a ring \( R \) is a submodule \( N \) such that for every finitely presented \( R \)-module \( F \), the induced map \( \mathrm{Hom}(F, N) \to \mathrm{Hom}(F, M) \) is injective. For example, in the abelian group \( \mathbb{Z} \), the subgroup \( 2\mathbb{Z} \subseteq \mathbb{Z} \) is pure because solving equations over \( \mathbb{Z} \) involving 2-divisibility remains consistent within \( 2\mathbb{Z} \). Contrasting torsion submodules, which contain elements annihilated by non-zero ring elements, pure submodules preserve exactness under tensor product functors, exemplified by the inclusion \( \mathbb{Z} \rightarrow \mathbb{Q} \) where \( \mathbb{Z} \) is a pure submodule of \( \mathbb{Q} \) but not torsion.
The Role of Torsion Submodules in Module Theory
Torsion submodules capture elements annihilated by nonzero elements of the ring, playing a crucial role in decomposing modules and analyzing their structure. They help identify the torsion part of a module, distinguishing it from torsion-free components and facilitating the classification over integral domains. Understanding torsion submodules is essential for studying purity, as pure submodules maintain exact sequences and can be torsion-free or contain torsion elements without disrupting module homomorphisms.
Applications and Importance of Pure Submodules
Pure submodules play a crucial role in module theory by preserving exact sequences under tensor products, which facilitates the analysis of module extensions and homological algebra. Unlike torsion submodules that capture elements annihilated by nonzero scalars, pure submodules maintain structural integrity, enabling applications in algebraic geometry and representation theory where flatness and base change properties are essential. The importance of pure submodules is evident in their use for constructing and characterizing flat modules, resolving purity conditions in rings, and advancing the study of decompositions in modules over integral domains.
Criteria for Identifying Torsion vs Pure Submodules
Torsion submodules consist of elements annihilated by nonzero elements of the ring, identified by the existence of a nonzero scalar multiplying the element to zero. Pure submodules are characterized by their preservation of exact sequences under tensoring, meaning a submodule \(N \subseteq M\) is pure if for every module \(X\), the induced map \(X \otimes N \to X \otimes M\) is injective. The key criterion distinguishing them is that torsion submodules capture elements with annihilators, while pure submodules ensure structural compatibility in exact sequences across tensor products.
Summary and Comparative Analysis
Torsion submodules consist of elements annihilated by some nonzero scalar, highlighting modules with locally finite annihilation properties, while pure submodules maintain exactness under tensoring, preserving structural embedding in larger modules. Torsion submodules primarily address element-specific annihilation, playing a crucial role in modules over integral domains, whereas pure submodules guarantee the preservation of algebraic relations, essential for module decomposition and extension problems. Comparative analysis reveals that torsion submodules identify intrinsic element limitations, whereas pure submodules emphasize homological and categorical stability within module theory frameworks.
Torsion submodule Infographic
 libterm.com
libterm.com