Deformation retract is a fundamental concept in topology where a space can be continuously shrunk to a subspace without changing its essential shape. This process preserves the homotopy type, enabling the study of complex spaces via simpler, more manageable ones. Explore the rest of the article to understand how deformation retracts reveal insights into the structure of topological spaces.
Table of Comparison
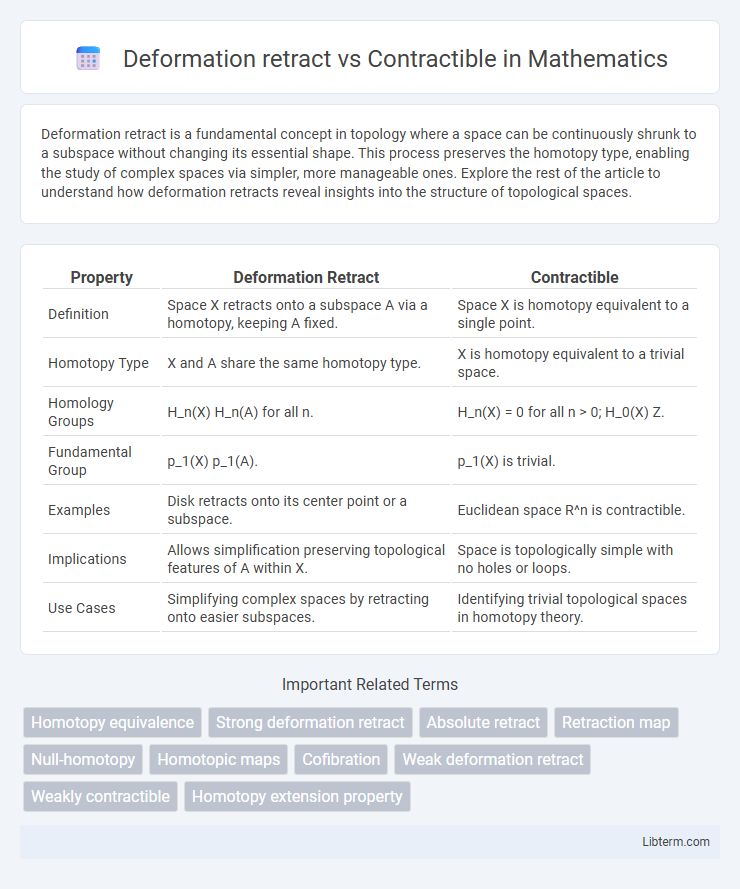
| Property | Deformation Retract | Contractible |
|---|---|---|
| Definition | Space X retracts onto a subspace A via a homotopy, keeping A fixed. | Space X is homotopy equivalent to a single point. |
| Homotopy Type | X and A share the same homotopy type. | X is homotopy equivalent to a trivial space. |
| Homology Groups | H_n(X) H_n(A) for all n. | H_n(X) = 0 for all n > 0; H_0(X) Z. |
| Fundamental Group | p_1(X) p_1(A). | p_1(X) is trivial. |
| Examples | Disk retracts onto its center point or a subspace. | Euclidean space R^n is contractible. |
| Implications | Allows simplification preserving topological features of A within X. | Space is topologically simple with no holes or loops. |
| Use Cases | Simplifying complex spaces by retracting onto easier subspaces. | Identifying trivial topological spaces in homotopy theory. |
Introduction to Deformation Retracts and Contractibility
Deformation retracts are continuous maps in topology that shrink a space onto a subspace while preserving homotopy type, serving as a strong form of homotopy equivalence. Contractible spaces are those homotopy equivalent to a single point, meaning they can be continuously shrunk to a point within the space. Understanding deformation retracts enables the identification of contractible spaces by showing how complex spaces reduce to simpler, contractible subspaces through homotopy.
Fundamental Concepts in Topological Spaces
Deformation retracts are continuous maps that shrink a topological space into a subspace while preserving homotopy type, ensuring the space and subspace have the same fundamental group and homotopy invariants. Contractible spaces are those homotopy equivalent to a point, meaning they have trivial fundamental groups and all higher homotopy groups vanish. Understanding deformation retracts clarifies how complex spaces reduce to simpler homotopy types, whereas contractibility implies the entire space can be continuously shrunk to a single point without changing its topological properties.
Definition of Deformation Retract
A deformation retract is a continuous map from a space onto a subspace that continuously shrinks the original space into the subspace while keeping the subspace fixed throughout the deformation. This concept is central in algebraic topology for simplifying spaces while preserving their homotopy type. Unlike contractible spaces, which can be continuously shrunk to a point, a deformation retract targets a specific subspace rather than a single point.
Understanding Contractible Spaces
Contractible spaces are those that can be continuously shrunk to a single point within the space, making them topologically trivial and homotopy equivalent to a point. Deformation retracts involve a continuous mapping that retracts a space onto a subspace while preserving homotopy type, showing that the original space shares the same topological features as the subspace. Understanding contractible spaces through deformation retracts reveals their fundamental simplicity, as any contractible space deformation retracts onto a point.
Key Differences Between Deformation Retracts and Contractible Spaces
Deformation retracts involve a continuous homotopy between a space and a subspace, preserving the subspace as a fixed point throughout the transformation, while contractible spaces are those homotopy equivalent to a single point, meaning they can be continuously shrunk to a point within the space itself. Key differences include that every contractible space is homotopy equivalent to a point, but a deformation retract need not reduce the entire space to a single point, only to a subspace with retained topological features. Contractibility implies trivial fundamental group and higher homotopy groups, whereas deformation retracts maintain more complex homotopy structures dependent on the retract subspace.
Examples Illustrating Deformation Retracts
A deformation retract is a continuous map that gradually shrinks a space into a subspace while preserving the homotopy type, such as the circle S^1 deforming onto a point or an interval retracting onto a midpoint. Contractible spaces like a disk D^2 can be deformation retracted to a single point, showing that being contractible implies the existence of a deformation retract to a point. Examples illustrating deformation retracts include the annulus retracting onto its central circle and a solid torus retracting onto its core circle, highlighting the role of deformation retracts in simplifying complex topological structures.
Examples of Contractible Spaces
Contractible spaces include familiar examples such as Euclidean spaces \(\mathbb{R}^n\), convex subsets of \(\mathbb{R}^n\), and cones over any topological space, all of which can be continuously shrunk to a point within the space. Unlike deformation retracts, which require the original space to retract onto a subspace homotopically, contractible spaces are homotopy equivalent to a single point, making their fundamental group trivial. These properties ensure that spheres \(S^n\) are not contractible, while spaces like disks \(D^n\) serve as classical contractible examples.
Relationship and Implications in Algebraic Topology
Deformation retracts provide a strong homotopy equivalence between a space and a subspace, implying the larger space shares the homotopy type with the subspace, while contractible spaces are those homotopy equivalent to a point. If a space deformation retracts onto a contractible subspace, the space itself is contractible, indicating trivial fundamental group and higher homotopy groups. This relationship is fundamental in algebraic topology for simplifying spaces while preserving homotopy invariants and computing homotopy groups.
Applications in Homotopy Theory
Deformation retracts serve as a fundamental tool in homotopy theory by simplifying complex spaces while preserving their homotopy type, enabling computational efficiency in topological invariants. Contractible spaces, characterized by homotopy equivalence to a single point, provide trivial homotopy groups, thus acting as base cases for homotopical classification. The interplay between deformation retracts and contractible spaces is crucial for constructing homotopy equivalences and analyzing fiber bundles, CW complexes, and fundamental groups in algebraic topology.
Summary: Deformation Retract vs Contractible Spaces
Deformation retracts are subspaces that can be continuously shrunk onto while remaining within the larger space, preserving homotopy type and providing a strong deformation equivalence. Contractible spaces are those homotopy equivalent to a single point, implying trivial fundamental groups and higher homotopy groups. Every contraction defines a deformation retract, but not all deformation retracts imply the entire space is contractible.
Deformation retract Infographic
 libterm.com
libterm.com