A symmetric monoidal category is a mathematical structure in category theory where objects and morphisms are equipped with a tensor product that is associative, has a unit object, and is symmetric, meaning the tensor product operation is commutative up to a natural isomorphism. This framework generalizes concepts from algebra and topology, providing a foundation for studying processes and systems that can be composed in parallel with interchangeable order. Explore the rest of the article to understand how symmetric monoidal categories are applied in areas like quantum computing and theoretical physics.
Table of Comparison
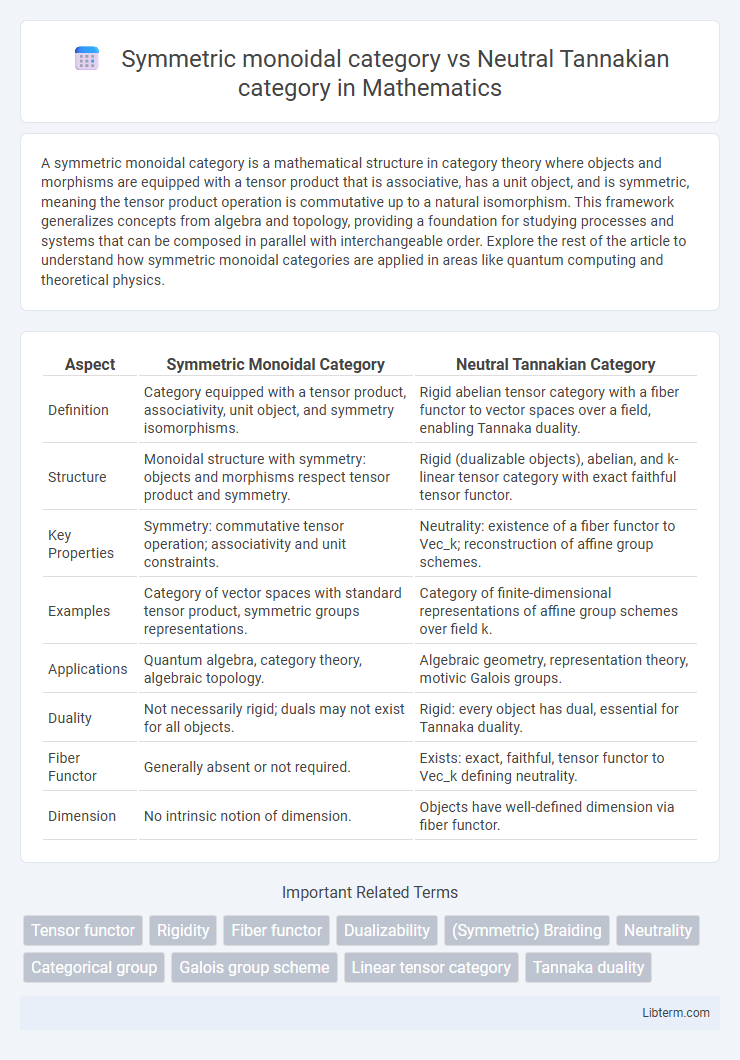
| Aspect | Symmetric Monoidal Category | Neutral Tannakian Category |
|---|---|---|
| Definition | Category equipped with a tensor product, associativity, unit object, and symmetry isomorphisms. | Rigid abelian tensor category with a fiber functor to vector spaces over a field, enabling Tannaka duality. |
| Structure | Monoidal structure with symmetry: objects and morphisms respect tensor product and symmetry. | Rigid (dualizable objects), abelian, and k-linear tensor category with exact faithful tensor functor. |
| Key Properties | Symmetry: commutative tensor operation; associativity and unit constraints. | Neutrality: existence of a fiber functor to Vec_k; reconstruction of affine group schemes. |
| Examples | Category of vector spaces with standard tensor product, symmetric groups representations. | Category of finite-dimensional representations of affine group schemes over field k. |
| Applications | Quantum algebra, category theory, algebraic topology. | Algebraic geometry, representation theory, motivic Galois groups. |
| Duality | Not necessarily rigid; duals may not exist for all objects. | Rigid: every object has dual, essential for Tannaka duality. |
| Fiber Functor | Generally absent or not required. | Exists: exact, faithful, tensor functor to Vec_k defining neutrality. |
| Dimension | No intrinsic notion of dimension. | Objects have well-defined dimension via fiber functor. |
Introduction to Symmetric Monoidal Categories
Symmetric monoidal categories are foundational structures in category theory characterized by a tensor product operation that is associative, unital, and symmetric up to natural isomorphism, allowing the interchange of objects without affecting the overall structure. These categories provide a framework to study algebraic and topological phenomena through functors preserving the monoidal structure, forming a basis for understanding neutral Tannakian categories. Neutral Tannakian categories further build upon symmetric monoidal categories by incorporating additional fiber functors and underlying field structures, enabling a powerful duality theory linking categories with affine group schemes.
Definition and Key Properties of Neutral Tannakian Categories
Neutral Tannakian categories are rigid abelian tensor categories equipped with a fiber functor to the category of finite-dimensional vector spaces over a field, allowing the reconstruction of affine group schemes via Tannaka duality. These categories are symmetric monoidal, meaning their tensor product is associative, commutative up to natural isomorphisms, and has a unit object, but they possess additional structures such as duals for every object and exactness properties essential for their Tannakian formalism. Unlike general symmetric monoidal categories, Neutral Tannakian categories enable an equivalence between the category and the representation category of a pro-algebraic group, capturing deep connections between category theory and algebraic geometry.
Core Differences: Structural Overview
A symmetric monoidal category is a category equipped with a tensor product, associativity, unit object, and symmetry natural isomorphisms satisfying coherence conditions, serving as a foundation for abstract tensor operations. A neutral Tannakian category is a rigid abelian symmetric monoidal category equipped with a fiber functor to vector spaces over a field, enabling reconstruction of affine group schemes via Tannaka duality. The core difference lies in the additional rigidity, abelian structure, and the existence of a fiber functor in neutral Tannakian categories, which links them to representation theory and group schemes, unlike the more general symmetric monoidal categories.
Symmetric Monoidal Categories: Examples and Applications
Symmetric monoidal categories provide a foundational framework in category theory where objects and morphisms can be tensored together with a symmetry constraint, enabling the modeling of commutative operations. Key examples include the category of vector spaces over a field with the tensor product and the category of sets with Cartesian product, which find applications in quantum computing, representation theory, and homotopy theory. These categories facilitate the study of structures with duals, traced monoidal categories, and symmetric operads, crucial for encoding algebraic and topological phenomena.
Neutral Tannakian Categories: Examples and Significance
Neutral Tannakian categories provide a powerful framework in category theory by facilitating the reconstruction of affine group schemes through tensor categories equipped with a fiber functor. Typical examples include the category of finite-dimensional representations of an affine group scheme over a field, which is symmetric monoidal, rigid, and abelian, satisfying additional exactness properties. Their significance lies in the Tannaka-Krein duality, enabling deep connections between algebraic geometry, representation theory, and category theory through explicit equivalences between neutral Tannakian categories and affine group schemes.
Functorial Perspectives: Fiber Functors in Tannakian Theory
Fiber functors in Neutral Tannakian categories serve as exact, faithful tensor functors to the category of finite-dimensional vector spaces, enabling the reconstruction of affine group schemes via their fiber functors. In contrast, symmetric monoidal categories broadly emphasize coherence conditions and tensor product structures without necessitating the existence of such fiber functors. The functorial perspective in Tannakian theory thus highlights how fiber functors provide a bridge between abstract categorical frameworks and concrete representation-theoretic objects.
Categorical Representations and Group Schemes
Symmetric monoidal categories provide a foundational framework for categorical representations by encoding tensor product structures compatible with symmetry constraints, enabling the study of monoidal functors and natural transformations. Neutral Tannakian categories, as rigid abelian symmetric monoidal categories equipped with a fiber functor to vector spaces, establish an equivalence with the category of representations of an affine group scheme over a field, thus linking categorical representations directly to group schemes. This correspondence enables reconstruction of the affine group scheme from the category itself, highlighting the deep interplay between categorical symmetries and group scheme structures in representation theory.
Role of Symmetry: Key Contrasts in Structure
Symmetric monoidal categories feature a braiding that satisfies a symmetry condition, meaning the tensor product commutes up to a natural isomorphism that is involutive. Neutral Tannakian categories, a special class of symmetric monoidal categories, possess additional structure characterized by fiber functors to vector spaces over a field, enabling a deep connection to affine group schemes via Tannakian duality. The role of symmetry in neutral Tannakian categories is pivotal for reconstructing the underlying group and ensuring compatibility with the associated tensor functor, contrasting with the more general and abstract symmetric braiding in ordinary symmetric monoidal categories.
Bridging Concepts: When is a Symmetric Monoidal Category Tannakian?
A symmetric monoidal category becomes Tannakian when it is abelian, rigid, and equipped with a fiber functor to the category of vector spaces over a field, satisfying exactness and compatibility with the tensor structure. This fiber functor enables reconstruction of an affine group scheme, linking the symmetric monoidal category to a neutral Tannakian category. The key bridging concept is the existence of a faithful, exact, k-linear tensor functor to vector spaces, ensuring the category is equivalent to the category of representations of an affine group scheme.
Applications and Implications in Modern Mathematics
Symmetric monoidal categories provide a foundational framework for tensorial structures in quantum algebra, topological quantum field theory, and category theory, enabling the abstraction of tensor products and symmetry constraints. Neutral Tannakian categories extend this framework by linking category theory to algebraic geometry and representation theory, allowing the reconstruction of affine group schemes from fiber functors and offering deep insights into the structure of motives and Galois groups. These categories have profound implications in modern mathematics by facilitating the study of symmetries in diverse algebraic and geometric settings, enabling the classification of algebraic groups through categorical methods, and advancing research in motives, non-abelian Hodge theory, and Langlands program.
Symmetric monoidal category Infographic
 libterm.com
libterm.com