Tangent space is a fundamental concept in differential geometry, representing the vector space that best approximates a manifold at a given point. It plays a crucial role in understanding the local behavior of curves and surfaces by capturing the directions in which one can tangentially pass through that point. Discover how tangent space influences various applications in mathematics and physics by exploring the rest of this article.
Table of Comparison
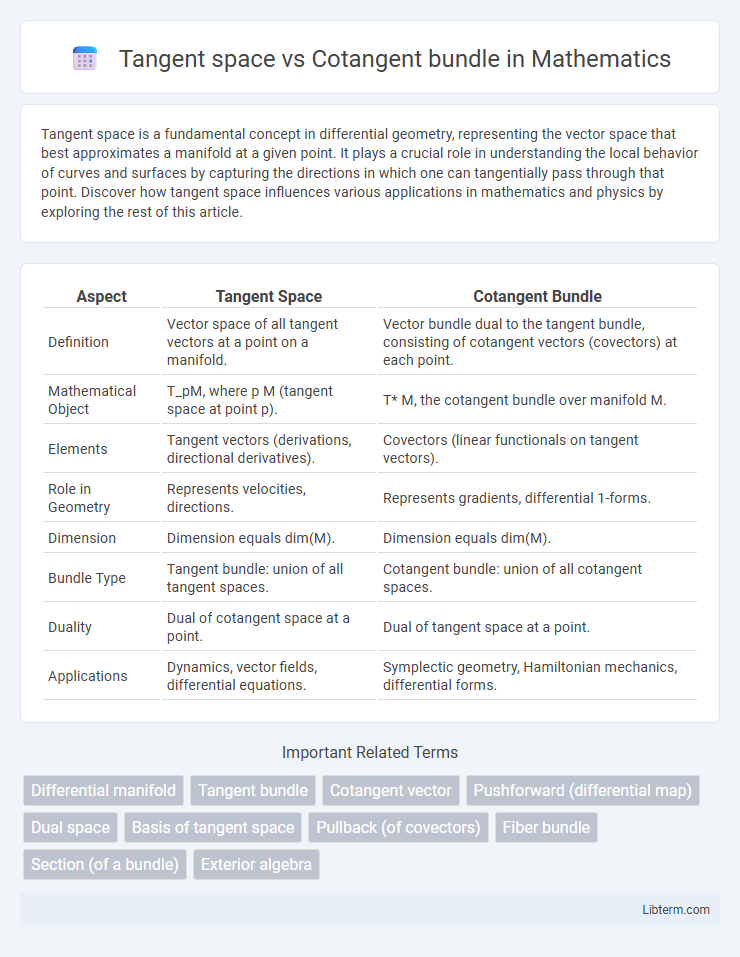
| Aspect | Tangent Space | Cotangent Bundle |
|---|---|---|
| Definition | Vector space of all tangent vectors at a point on a manifold. | Vector bundle dual to the tangent bundle, consisting of cotangent vectors (covectors) at each point. |
| Mathematical Object | T_pM, where p M (tangent space at point p). | T* M, the cotangent bundle over manifold M. |
| Elements | Tangent vectors (derivations, directional derivatives). | Covectors (linear functionals on tangent vectors). |
| Role in Geometry | Represents velocities, directions. | Represents gradients, differential 1-forms. |
| Dimension | Dimension equals dim(M). | Dimension equals dim(M). |
| Bundle Type | Tangent bundle: union of all tangent spaces. | Cotangent bundle: union of all cotangent spaces. |
| Duality | Dual of cotangent space at a point. | Dual of tangent space at a point. |
| Applications | Dynamics, vector fields, differential equations. | Symplectic geometry, Hamiltonian mechanics, differential forms. |
Introduction to Tangent Spaces and Cotangent Bundles
Tangent spaces at a point on a differentiable manifold consist of all possible directional derivatives, forming a vector space associated with that point. The cotangent bundle is the dual vector bundle composed of all cotangent spaces, which are linear functionals acting on tangent vectors. Understanding these structures is essential for differential geometry and provides the foundation for concepts such as differential forms and manifold integration.
Fundamental Concepts in Differential Geometry
The tangent space at a point on a smooth manifold consists of all possible velocity vectors of curves passing through that point, forming a vector space that captures directional derivatives. The cotangent bundle, dual to the tangent bundle, comprises all covectors or linear functionals acting on tangent vectors, essential for defining differential forms and integrating on manifolds. Understanding the interplay between tangent spaces and the cotangent bundle is fundamental in differential geometry, facilitating notions of gradients, differentials, and tensor fields.
Defining the Tangent Space at a Point
The tangent space at a point on a differentiable manifold is a vector space consisting of all possible directional derivatives at that point, representing velocities of curves passing through it. Its dual space, the cotangent space, consists of all linear functionals acting on these tangent vectors, critical for defining differential forms and gradients. Formal construction of the tangent space uses equivalence classes of curves or derivations, providing a local linear approximation to the manifold structure.
Visualizing the Tangent Space: Examples and Intuition
Tangent space at a point on a manifold consists of all possible velocity vectors of curves passing through that point, providing a linear approximation of the manifold near that point. Visualizing tangent spaces can be achieved through examples such as the tangent plane to a sphere, where each tangent vector represents a direction in which one can move infinitesimally from the point on the surface. Intuition is enhanced by imagining tangent vectors as arrows attached to a point, capturing local geometric information essential for fields like differential geometry and physics.
The Cotangent Bundle: Structure and Significance
The cotangent bundle is a fundamental geometric construct comprising all cotangent spaces at each point of a smooth manifold, forming a 2n-dimensional manifold for an n-dimensional base manifold. It serves as the natural domain for differential 1-forms and plays a central role in symplectic geometry and classical mechanics by providing the phase space structure crucial for Hamiltonian dynamics. This bundle's canonical symplectic form enables the translation of geometric problems into algebraic terms, facilitating advanced analysis in differential geometry and mathematical physics.
Algebraic Properties of Tangent Spaces vs. Cotangent Bundles
Tangent spaces at a point on a manifold form vector spaces that capture directional derivatives and support operations such as vector addition and scalar multiplication, reflecting their structure as modules over the real numbers. Cotangent bundles, composed of the dual spaces to tangent spaces, consist of covectors that act as linear functionals on tangent vectors and inherit an algebraic structure enabling differential forms and the exterior algebra construction. The duality between tangent spaces and cotangent bundles underpins many geometric constructions, with tangent spaces enabling differentiation of curves and cotangent bundles facilitating the definition of differential forms and symplectic geometry.
Applications in Physics: Velocity vs. Momentum Spaces
Tangent spaces represent velocity vectors at a point on a manifold, crucial for describing motion and kinematics in classical mechanics, while cotangent bundles model momentum spaces essential in Hamiltonian mechanics and symplectic geometry. The duality between tangent and cotangent spaces facilitates transformations between velocity and momentum, enabling canonical formulations of physical laws. Applications include phase space analysis, where cotangent bundles provide the natural framework for conserved quantities and symmetries in quantum and classical systems.
Mapping between Tangent and Cotangent Spaces
The tangent space at a point on a smooth manifold consists of directional derivatives representing velocities, while the cotangent space comprises linear functionals acting on these tangent vectors. The mapping between tangent and cotangent spaces is facilitated by the Riemannian metric, which establishes an isomorphism via the musical isomorphisms "flat" () and "sharp" (#) operators, converting vectors to covectors and vice versa. This duality is essential in differential geometry and physics, enabling operations such as raising and lowering indices in tensor calculus.
Role in Differential Forms and Calculus on Manifolds
The tangent space at a point on a manifold consists of all possible velocity vectors of curves passing through that point, serving as the domain for directional derivatives and vector fields in calculus on manifolds. The cotangent bundle, composed of all cotangent spaces, provides the natural setting for differential 1-forms and covectors, enabling integration and the formulation of exterior derivatives critical to differential forms theory. Together, these structures facilitate the duality between vectors and covectors, underpinning operations like pullbacks, pushforwards, and the general calculus of differential forms on smooth manifolds.
Key Differences and Summary Comparison
The tangent space at a point on a differentiable manifold consists of all possible velocity vectors of curves passing through that point, forming a vector space of directional derivatives. In contrast, the cotangent bundle is composed of all cotangent spaces, each being the dual space to the tangent space at a point, containing linear functionals that map tangent vectors to real numbers. The key difference lies in their roles: tangent spaces represent directions and velocities, while cotangent bundles consist of covectors or differential 1-forms that enable integration and define gradients.
Tangent space Infographic
 libterm.com
libterm.com