Reduced homology refines ordinary homology by adjusting the calculation of the zero-dimensional homology group, providing a more nuanced understanding of the topological structure of a space. This adjustment helps in distinguishing between connected components and the basepoint, making it essential for certain algebraic topology applications. Explore the rest of the article to gain a deeper insight into how reduced homology enhances topological analysis and its practical uses.
Table of Comparison
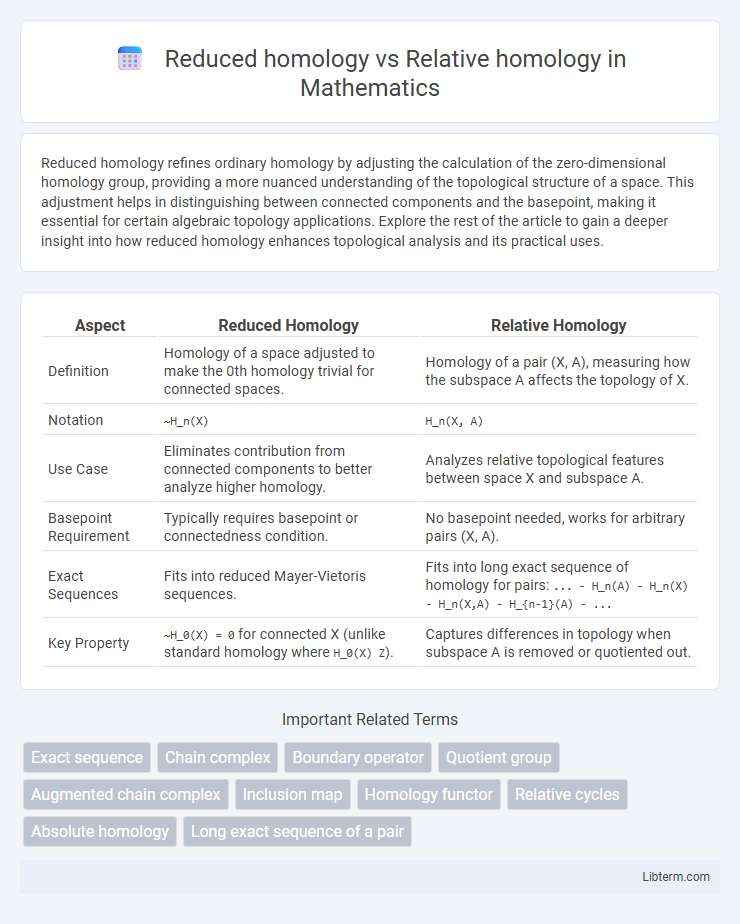
| Aspect | Reduced Homology | Relative Homology |
|---|---|---|
| Definition | Homology of a space adjusted to make the 0th homology trivial for connected spaces. | Homology of a pair (X, A), measuring how the subspace A affects the topology of X. |
| Notation | ~H_n(X) |
H_n(X, A) |
| Use Case | Eliminates contribution from connected components to better analyze higher homology. | Analyzes relative topological features between space X and subspace A. |
| Basepoint Requirement | Typically requires basepoint or connectedness condition. | No basepoint needed, works for arbitrary pairs (X, A). |
| Exact Sequences | Fits into reduced Mayer-Vietoris sequences. | Fits into long exact sequence of homology for pairs: ... - H_n(A) - H_n(X) - H_n(X,A) - H_{n-1}(A) - ... |
| Key Property | ~H_0(X) = 0 for connected X (unlike standard homology where H_0(X) Z). |
Captures differences in topology when subspace A is removed or quotiented out. |
Introduction to Homology in Topology
Reduced homology modifies the standard homology groups by adjusting the dimension-zero groups to better handle connected spaces, often ensuring that a single-point space has trivial reduced homology. Relative homology studies the homology of a pair of topological spaces \( (X, A) \), capturing how the space \( X \) changes when a subspace \( A \) is collapsed, leading to long exact sequences that link absolute and relative homology groups. Both concepts extend classical homology theory in algebraic topology, providing refined tools to analyze topological spaces' structure and relationships.
Overview of Reduced Homology
Reduced homology provides an adjustment to standard homology by modifying the 0th homology group to better handle the connectedness of spaces, often used to simplify calculations involving connected components. It differs from relative homology, which studies the homological features of a space relative to a subspace, focusing on the difference between them. By using reduced homology, topologists can more effectively distinguish between spaces that are simply connected and those that are not, particularly when analyzing pointed spaces or wedge sums.
Fundamentals of Relative Homology
Relative homology studies the homology groups of a topological space X relative to a subspace A, capturing how cycles in X behave modulo those in A, formally defined as H_n(X, A). This approach allows for analyzing the difference in homological features between X and A, providing crucial insights beyond absolute homology by examining pairs of spaces. Reduced homology, denoted \(\tilde{H}_n(X)\), modifies standard homology to adjust the homology of a point to zero, while relative homology generalizes this concept by relating the topology of two spaces simultaneously.
Key Differences Between Reduced and Relative Homology
Reduced homology modifies standard homology groups by adjusting the 0th homology group, ensuring a trivial group for a single point space, which simplifies calculations in connected spaces. Relative homology compares the homology of a space and its subspace, capturing features lost when passing from the larger space to the subspace by considering chain complexes modulo the subspace. Key differences include that reduced homology alters absolute homology groups for connectedness normalization, while relative homology encodes the relationship between a space and its subspace, providing insights into how subspaces influence overall topology.
Algebraic Definitions and Notations
Reduced homology \(\tilde{H}_n(X)\) differs from relative homology \(H_n(X,A)\) primarily in its algebraic construction and notation: reduced homology is derived by augmenting the chain complex with an extra boundary map to the integers \(\mathbb{Z}\), effectively adjusting the zeroth homology group to capture connectedness without basepoint dependence. Relative homology is defined from the quotient chain complex \(C_n(X)/C_n(A)\), where \(A \subseteq X\), forming the groups \(H_n(X,A) = H_n(C_*(X)/C_*(A))\) to measure cycles in \(X\) modulo those in \(A\). Notationally, reduced homology simplifies to \(\tilde{H}_n(X) \cong H_n(X, \{*\})\) when a basepoint \(*\) is chosen, bridging reduced and relative homology through exact sequences of the pair \((X, *)\).
Applications of Reduced Homology
Reduced homology refines standard homology by adjusting dimension-zero groups to better handle connected components, making it essential in topological data analysis for distinguishing shapes with a single connected component. Its applications extend to simplifying invariants in algebraic topology, facilitating computations in simplicial complexes, and improving persistence homology algorithms used in data classification and shape recognition. Reduced homology's ability to provide finer resolution in Betti number calculations enhances analysis in computational geometry and network topology.
Use Cases for Relative Homology
Relative homology is particularly useful for analyzing topological spaces with subspaces, enabling the study of how features in a space change when a subset is removed or identified, such as in the Mayer-Vietoris sequence or excision theorem. It is instrumental in solving problems involving pairs of spaces, like manifolds with boundary, allowing computations of invariants that capture boundary behavior or local properties around substructures. Reduced homology, by contrast, simplifies calculations for connected spaces by modifying the zeroth homology but lacks the nuanced context provided by pairs of spaces inherent in relative homology's applications.
Examples Illustrating Both Homology Types
Reduced homology for a space X modifies the 0th homology group, typically yielding \(\tilde{H}_0(X) = 0\) for connected spaces, such as \( \tilde{H}_0(S^1) = 0 \) for the circle. Relative homology \(H_*(X,A)\) measures the homology of a space X relative to a subspace A, exemplified by the pair \((D^2, S^1)\) where \(H_2(D^2, S^1) \cong \mathbb{Z}\) captures the two-dimensional hole filled by the disk. Reduced homology collapses the basepoint to zero, while relative homology tracks how attaching the subspace alters cycles and boundaries, crucial for understanding inclusion maps and excision in algebraic topology.
Advantages and Limitations
Reduced homology simplifies calculations by adjusting the homology groups of a space to account for its connected components, making it especially useful in distinguishing between contractible and non-contractible spaces; however, it is limited in handling pairs of spaces where relative topology plays a crucial role. Relative homology provides a framework for comparing a topological space with a subspace, capturing information about features that exist relative to that subspace, which makes it advantageous in studying inclusions and excisions but can lead to more complex computations and less intuitive interpretations than reduced homology. Both theories contribute valuable insights: reduced homology excels in simplifying absolute invariants, whereas relative homology is indispensable for analyzing topological relationships within pairs.
Conclusion and Further Reading
Reduced homology refines standard homology by adjusting the 0th homology group to better handle connected spaces, while relative homology studies pairs of spaces to capture features of a subspace within a larger space. Reduced homology often simplifies calculations in connected complexes, whereas relative homology provides critical insights into inclusion maps and excision properties. For deeper understanding, consult Allen Hatcher's "Algebraic Topology" and the relevant chapters on homology theories and exact sequences.
Reduced homology Infographic
 libterm.com
libterm.com