Upper triangular matrices have all elements below the main diagonal equal to zero, simplifying many matrix operations such as solving linear equations through back substitution. These matrices play a crucial role in numerical methods, including LU decomposition and matrix factorization, enhancing computational efficiency. Explore the rest of this article to understand how upper triangular matrices impact your calculations and algorithms.
Table of Comparison
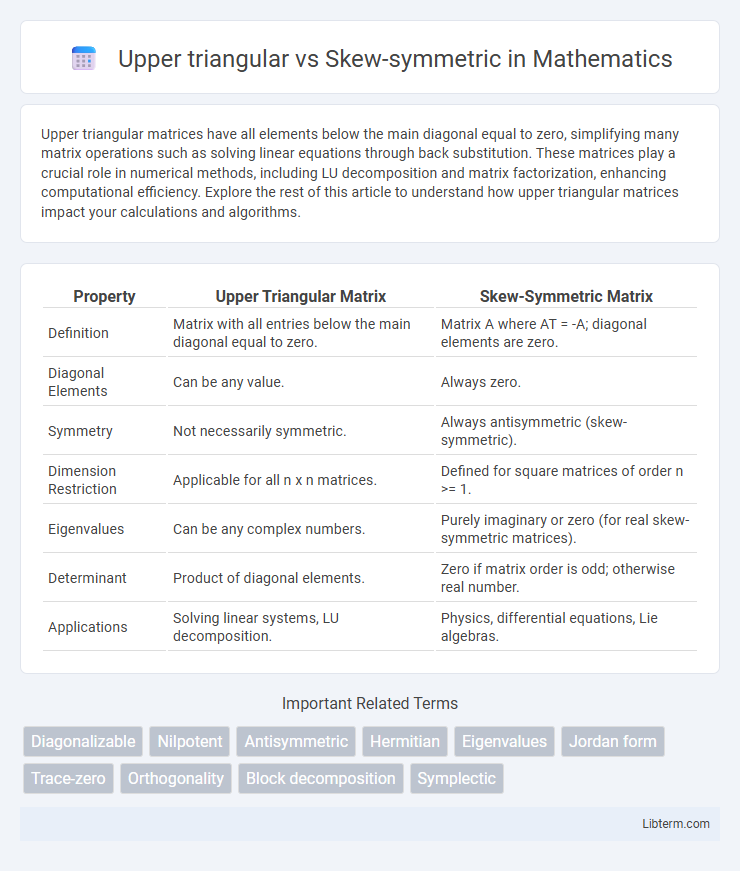
| Property | Upper Triangular Matrix | Skew-Symmetric Matrix |
|---|---|---|
| Definition | Matrix with all entries below the main diagonal equal to zero. | Matrix A where AT = -A; diagonal elements are zero. |
| Diagonal Elements | Can be any value. | Always zero. |
| Symmetry | Not necessarily symmetric. | Always antisymmetric (skew-symmetric). |
| Dimension Restriction | Applicable for all n x n matrices. | Defined for square matrices of order n >= 1. |
| Eigenvalues | Can be any complex numbers. | Purely imaginary or zero (for real skew-symmetric matrices). |
| Determinant | Product of diagonal elements. | Zero if matrix order is odd; otherwise real number. |
| Applications | Solving linear systems, LU decomposition. | Physics, differential equations, Lie algebras. |
Introduction to Matrix Types
Upper triangular matrices consist of elements above and including the main diagonal, with all entries below the diagonal equal to zero, commonly used in solving linear systems and matrix factorization. Skew-symmetric matrices satisfy the condition A^T = -A, meaning their diagonal elements are zero and they represent important structures in physics and geometry, especially in rotations and antisymmetric transformations. Both matrix types exhibit unique properties influencing their applications in matrix theory and computational algorithms.
Defining Upper Triangular Matrices
Upper triangular matrices are square matrices where all elements below the main diagonal are zero, meaning entries a_ij = 0 for all i > j. This structure simplifies matrix operations such as solving linear systems and computing determinants, as the determinant equals the product of the diagonal elements. In contrast, skew-symmetric matrices satisfy the property A^T = -A, typically having zero diagonal entries, distinguishing them fundamentally from upper triangular matrices by their antisymmetric behavior.
Understanding Skew-Symmetric Matrices
Skew-symmetric matrices are square matrices where the transpose equals the negative of the original matrix, meaning \(A^T = -A\) and all diagonal elements are zero. Unlike upper triangular matrices, which have all elements below the main diagonal equal to zero, skew-symmetric matrices exhibit antisymmetry, making them vital in fields like physics for representing rotational transformations. Understanding skew-symmetric matrices involves recognizing their unique structural properties, eigenvalues that are purely imaginary or zero, and their role in Lie algebra and matrix exponentiation.
Key Properties of Upper Triangular Matrices
Upper triangular matrices are square matrices where all entries below the main diagonal are zero, allowing for simplified matrix operations such as forward substitution in linear systems. They possess properties like easy determinant calculation as the product of diagonal elements and stability under matrix multiplication when multiplied by other upper triangular matrices. Unlike skew-symmetric matrices, which are defined by the property \( A^T = -A \) and have zero diagonal entries, upper triangular matrices do not necessarily have symmetric or antisymmetric characteristics.
Essential Properties of Skew-Symmetric Matrices
Skew-symmetric matrices have the essential property that the transpose of the matrix equals its negative, expressed as \(A^T = -A\), ensuring all diagonal elements are zero. Unlike upper triangular matrices, which have non-zero entries only above the main diagonal, skew-symmetric matrices exhibit antisymmetry, meaning \(a_{ij} = -a_{ji}\) for all \(i, j\). This property leads to eigenvalues that are either zero or purely imaginary, distinguishing skew-symmetric matrices in spectral analysis from the structure of upper triangular matrices.
Structural Differences: Upper Triangular vs Skew-Symmetric
Upper triangular matrices have all entries below the main diagonal equal to zero, with no specific symmetry constraints on the diagonal or above. Skew-symmetric matrices are square matrices where the transpose equals the negative of the original matrix, enforcing all diagonal elements to be zero and creating an antisymmetric structure across the diagonal. The fundamental structural difference lies in the pattern of zero elements: upper triangular zeros below the diagonal, skew-symmetric zeros on the diagonal with antisymmetry across it.
Applications in Mathematical Computations
Upper triangular matrices simplify solving linear systems through efficient back substitution methods, significantly reducing computational complexity in numerical linear algebra. Skew-symmetric matrices are essential in representing and analyzing rotational transformations and have applications in physics, particularly in describing angular velocities and antisymmetric bilinear forms. Both matrix types play crucial roles in optimizing algorithms for eigenvalue problems, stability analysis, and matrix factorizations in advanced mathematical computations.
Eigenvalues and Determinants Comparison
Upper triangular matrices have eigenvalues explicitly given by their diagonal entries, making determinant calculation straightforward as the product of these diagonal elements. Skew-symmetric matrices, characterized by A^T = -A, possess purely imaginary eigenvalues or zeros in the real case, and their determinants are nonnegative, often computed through Pfaffians in even dimensions. While upper triangular matrices may have complex or real eigenvalues, skew-symmetric matrices exhibit spectral properties reflecting their antisymmetry, leading to distinct eigenvalue distributions and determinant behaviors.
Real-World Examples and Use Cases
Upper triangular matrices are essential in numerical methods such as solving linear systems and matrix decompositions like LU and QR, widely used in engineering simulations and computer graphics transformations. Skew-symmetric matrices find applications in physics, representing rotational dynamics and angular velocity tensors in rigid body motion and robotics control systems. Both matrix types enable efficient computation and model complex real-world phenomena, with upper triangular matrices facilitating algorithmic stability and skew-symmetric matrices encoding antisymmetric relationships in vector calculus.
Conclusion: Choosing the Right Matrix Type
Upper triangular matrices are ideal for solving linear systems and simplifying matrix operations due to their zero elements below the diagonal, enhancing computational efficiency. Skew-symmetric matrices, defined by the property A^T = -A, are crucial in physics and engineering applications involving rotational dynamics and antisymmetric relations. Selecting between these matrix types depends on the problem context: use upper triangular matrices for algorithmic convenience in numerical methods, while skew-symmetric matrices suit modeling antisymmetric phenomena.
Upper triangular Infographic
 libterm.com
libterm.com