Uniforms play a crucial role in creating a cohesive and professional appearance that fosters team spirit and brand identity across organizations. They enhance security by making it easy to identify members of a group and reduce distractions caused by varied attire. Explore the full article to discover how uniforms can positively impact your workplace environment and culture.
Table of Comparison
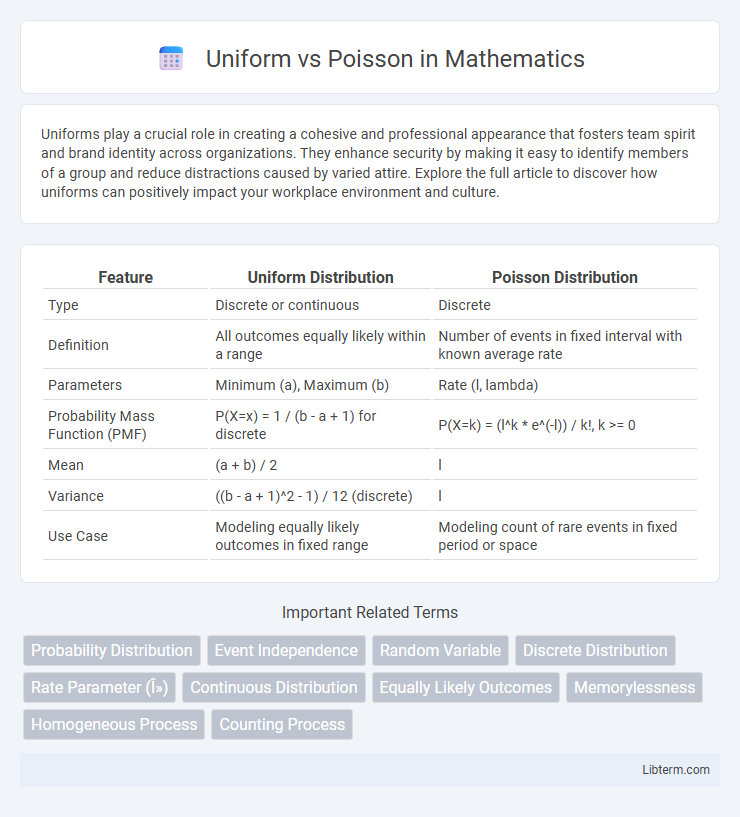
| Feature | Uniform Distribution | Poisson Distribution |
|---|---|---|
| Type | Discrete or continuous | Discrete |
| Definition | All outcomes equally likely within a range | Number of events in fixed interval with known average rate |
| Parameters | Minimum (a), Maximum (b) | Rate (l, lambda) |
| Probability Mass Function (PMF) | P(X=x) = 1 / (b - a + 1) for discrete | P(X=k) = (l^k * e^(-l)) / k!, k >= 0 |
| Mean | (a + b) / 2 | l |
| Variance | ((b - a + 1)^2 - 1) / 12 (discrete) | l |
| Use Case | Modeling equally likely outcomes in fixed range | Modeling count of rare events in fixed period or space |
Introduction to Probability Distributions
Uniform and Poisson distributions serve distinct roles in probability theory; the uniform distribution models equally likely outcomes within a fixed range, whereas the Poisson distribution describes the probability of a given number of events occurring in a fixed interval of time or space. The uniform distribution is continuous or discrete with constant probability density or mass, making it ideal for scenarios requiring equal likelihood, such as random sampling. Conversely, the Poisson distribution, characterized by its rate parameter l (lambda), is discrete and often applied to count events, such as arrival rates in queueing theory or number of mutations in genetics.
Overview of Uniform Distribution
The uniform distribution, also known as the rectangular distribution, is a continuous probability distribution where all outcomes are equally likely within a defined range [a, b]. Its probability density function (PDF) is constant, calculated as 1/(b-a), reflecting equal probability for every value in the interval. The uniform distribution is widely used in simulations, random sampling, and scenarios requiring unbiased variability over a specified domain.
Overview of Poisson Distribution
Poisson distribution models the probability of a given number of events occurring in a fixed interval of time or space, assuming the events happen independently at a constant average rate. It is characterized by the parameter l (lambda), representing the expected number of occurrences within the interval. Unlike the uniform distribution, which assumes equal probability across outcomes, Poisson distribution is skewed and discrete, often used in fields like telecommunications, traffic flow analysis, and queuing theory.
Key Differences: Uniform vs Poisson
The Uniform distribution assigns equal probability to all outcomes within a specific range, making it ideal for modeling events with consistent chances. In contrast, the Poisson distribution models the probability of a given number of events occurring within a fixed interval of time or space, particularly useful for rare or random occurrences. Key differences include the Uniform distribution's constant probability density versus the Poisson's discrete probabilities based on event rates, and Uniform being continuous or discrete, whereas Poisson is strictly discrete.
Applications of Uniform Distribution
Uniform distribution is widely applied in scenarios requiring equal probability outcomes, such as random number generation, cryptographic key selection, and simulation modeling. It supports unbiased sampling in statistical experiments and quality control processes by providing a consistent likelihood across all intervals within a dataset. Uniform distribution also plays a crucial role in computer graphics for texture mapping and in algorithms requiring randomized inputs with no preferential weighting.
Applications of Poisson Distribution
Poisson distribution is widely used in fields such as telecommunications, traffic engineering, and natural disaster modeling to predict the number of events occurring within a fixed interval of time or space. It accurately models rare events like the number of phone calls received by a call center per minute or the count of radioactive particle emissions detected in a given period. This distribution is especially useful when the events occur independently and at a constant average rate, distinguishing it from uniform distribution which assumes equally likely occurrences across an interval.
Mathematical Formulation and Properties
The uniform distribution is defined by a constant probability density function \( f(x) = \frac{1}{b-a} \) for \( x \) in the interval \([a, b]\), characterized by equal likelihood over a finite range, with mean \( \mu = \frac{a+b}{2} \) and variance \( \sigma^2 = \frac{(b-a)^2}{12} \). The Poisson distribution models discrete event counts occurring independently within a fixed interval, with probability mass function \( P(k; \lambda) = \frac{\lambda^k e^{-\lambda}}{k!} \), where \( \lambda \) is the average event rate, and both mean and variance equal \( \lambda \). Uniform distribution exhibits continuous and bounded behavior with zero skewness, while Poisson is discrete, unbounded on the non-negative integers, and skewed for smaller \( \lambda \), converging to normality as \( \lambda \) increases.
Real-World Examples and Use Cases
Uniform distribution models scenarios with equal probability outcomes, such as rolling a fair die or selecting a random lottery number, making it useful in simulations and randomized algorithms. Poisson distribution applies to events occurring independently over a fixed interval, exemplified by modeling the number of emails received per hour or traffic flow at a toll booth, aiding in queue management and reliability testing. Businesses leverage uniform distribution for fair sampling techniques while utilizing Poisson distribution to predict occurrences in fields like telecommunications, healthcare, and risk assessment.
Choosing the Right Distribution for Data Modeling
Choosing the right distribution for data modeling depends on the nature and characteristics of the dataset; Uniform distribution suits scenarios with equally likely outcomes over a continuous range, ideal for random sampling or simulation when all events have the same probability. Poisson distribution effectively models the number of events occurring within a fixed interval of time or space, especially for rare events or count data where occurrences are independent and happen at a constant average rate. Understanding the data pattern--whether it is continuous with equal likelihood or discrete event counts--is crucial for selecting between Uniform and Poisson distributions to ensure accurate modeling and predictive analysis.
Conclusion: Comparing Uniform and Poisson
The Uniform distribution models data with equal probability across a fixed range, making it ideal for scenarios with limited variability and fixed outcomes. The Poisson distribution effectively captures the frequency of rare events occurring independently within a fixed interval, suited for count data and event occurrence modeling. Comparing both, Uniform is best for continuous, evenly spread data, whereas Poisson excels in discrete, event-based contexts with variable event rates.
Uniform Infographic
 libterm.com
libterm.com