Recursively Enumerable Languages are a fundamental concept in computational theory, representing languages for which a Turing machine can enumerate all valid strings, though it may not halt on invalid inputs. These languages capture the idea of semi-decidability, where membership can be confirmed but not always rejected conclusively. Explore the rest of the article to understand how Recursively Enumerable Languages influence computational limits and automata theory.
Table of Comparison
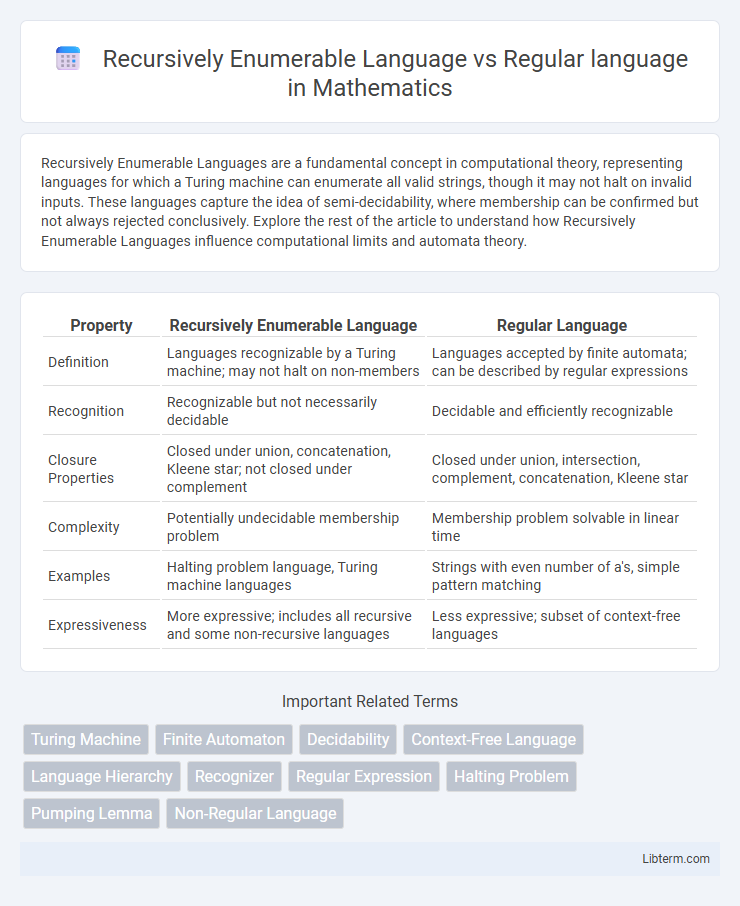
| Property | Recursively Enumerable Language | Regular Language |
|---|---|---|
| Definition | Languages recognizable by a Turing machine; may not halt on non-members | Languages accepted by finite automata; can be described by regular expressions |
| Recognition | Recognizable but not necessarily decidable | Decidable and efficiently recognizable |
| Closure Properties | Closed under union, concatenation, Kleene star; not closed under complement | Closed under union, intersection, complement, concatenation, Kleene star |
| Complexity | Potentially undecidable membership problem | Membership problem solvable in linear time |
| Examples | Halting problem language, Turing machine languages | Strings with even number of a's, simple pattern matching |
| Expressiveness | More expressive; includes all recursive and some non-recursive languages | Less expressive; subset of context-free languages |
Introduction to Formal Languages
Recursively enumerable languages encompass all languages recognizable by a Turing machine, including those that are not decidable, while regular languages represent the simplest class of formal languages recognizable by finite automata. In formal language theory, regular languages are defined by regular expressions and have closure under union, concatenation, and Kleene star operations, whereas recursively enumerable languages require more powerful computational models for recognition. Understanding the distinction between these language classes is fundamental in automata theory and computational complexity, highlighting varying levels of language decidability and recognizability.
Overview of Regular Languages
Regular languages are a fundamental class of formal languages characterized by their simplicity and efficient recognizability using finite automata. They can be described by regular expressions and generated by regular grammars, making them suitable for pattern matching and lexical analysis. Despite their expressive limitations compared to recursively enumerable languages, regular languages offer decidable membership problems and can be processed in linear time.
Exploring Recursively Enumerable Languages
Recursively enumerable languages represent a broader class of languages than regular languages, characterized by their recognition through Turing machines that may not halt on all inputs. Unlike regular languages, which are defined and accepted by finite automata with decidable membership, recursively enumerable languages encompass problems where membership can be semi-decided but not always conclusively determined. Exploring recursively enumerable languages involves understanding their relation to Turing machine computability, the Halting Problem, and their pivotal role in formal language theory and computational complexity.
Defining Characteristics and Differences
Recursively enumerable languages are defined by Turing machines that accept strings by eventually halting on members, allowing recognition of a broader class of languages than regular languages, which are recognized by finite automata with limited memory. Regular languages have strict structural limitations and can be described using regular expressions or deterministic finite automata, making them decidable and efficiently recognizable. The key difference lies in computational power and decidability: all regular languages are decidable and a subset of recursively enumerable languages, whereas recursively enumerable languages may be undecidable and encompass more complex patterns beyond the capabilities of finite automata.
Recognizers: Finite Automata vs Turing Machines
Regular languages are recognized by finite automata, which operate with limited memory and process input strings in linear time, making them efficient but unable to handle complex computations. Recursively enumerable languages are recognized by Turing machines, which possess unlimited memory and can simulate any algorithm, allowing them to accept a broader class of languages including those beyond regular or context-free languages. Finite automata provide quick recognition for simple patterns, whereas Turing machines serve as powerful recognizers capable of deciding membership for languages requiring unbounded computational resources.
Language Closure Properties Comparison
Recursively enumerable languages exhibit closure under union, concatenation, and Kleene star but are not closed under complementation, whereas regular languages maintain closure under union, concatenation, Kleene star, complementation, and intersection. The closure properties of regular languages are supported by finite automata and regular expressions, enabling efficient language operations. Recursively enumerable languages rely on Turing machines, which impact their closure properties, particularly the lack of closure under complementation due to undecidability.
Decidability and Computability Aspects
Recursively enumerable languages are recognized by Turing machines but are not necessarily decidable, meaning there is no guaranteed algorithm to halt on all inputs; regular languages, recognized by finite automata, are always decidable and have efficient algorithms for membership testing. Decidability in regular languages is straightforward due to their closure properties and simple structure, while recursively enumerable languages can encode complex computations where halting may be undecidable. Computability in regularly languages is limited to patterns definable by regular expressions, contrasting with the broader, more computationally powerful scope of recursively enumerable languages.
Examples of Regular and Recursively Enumerable Languages
Regular languages include examples such as the set of all strings over {a, b} containing an even number of a's and the language consisting of all strings that start with the symbol '0.' Recursively enumerable languages extend beyond regular languages, including more complex sets like the language of all Turing machines that halt on a given input and the classic Halting problem language. While regular languages are recognized by finite automata, recursively enumerable languages are recognized by Turing machines, enabling them to capture a broader range of computational problems.
Practical Applications and Implications
Regular languages enable efficient parsing and pattern matching in tools like lexical analyzers and text editors, ensuring fast and predictable computation with finite automata. Recursively enumerable languages support broader computational models such as Turing machines, facilitating applications in automated theorem proving, programming language semantics, and decision problems that require recognition of more complex structures. While regular languages excel in simplicity and speed for basic syntax analysis, recursively enumerable languages underpin advanced formal verification and language recognition tasks where undecidability and infinite computation may arise.
Summary Table: Regular vs Recursively Enumerable Languages
Regular languages are characterized by finite automata and can be recognized with deterministic or nondeterministic state machines, making them computationally simple and efficiently decidable. Recursively enumerable languages, recognized by Turing machines, encompass a broader class with the ability to represent all languages that a computer program can identify, though membership may be undecidable. The summary table highlights that regular languages are closed under union, intersection, and complement with guaranteed termination, whereas recursively enumerable languages are closed only under union and intersection but lack decidability in complement and membership problems.
Recursively Enumerable Language Infographic
 libterm.com
libterm.com