Hyperbolic language amplifies meaning by using exaggeration to emphasize emotions or ideas, making communication more vivid and engaging. This rhetorical device enhances persuasion and adds dramatic effect to both spoken and written content. Explore the rest of the article to understand how hyperbolic expressions can enrich your communication skills.
Table of Comparison
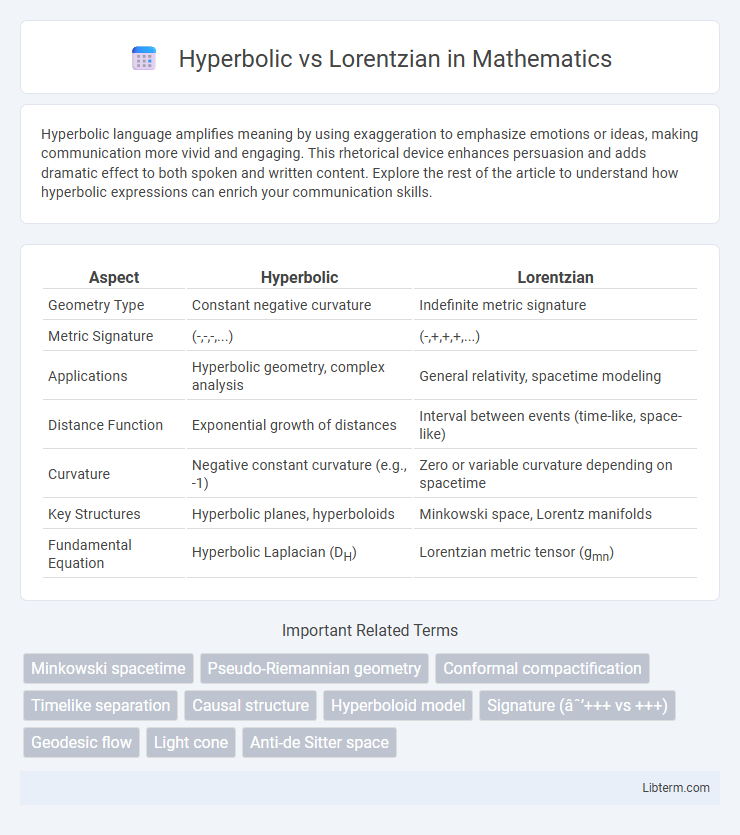
| Aspect | Hyperbolic | Lorentzian |
|---|---|---|
| Geometry Type | Constant negative curvature | Indefinite metric signature |
| Metric Signature | (-,-,-,...) | (-,+,+,+,...) |
| Applications | Hyperbolic geometry, complex analysis | General relativity, spacetime modeling |
| Distance Function | Exponential growth of distances | Interval between events (time-like, space-like) |
| Curvature | Negative constant curvature (e.g., -1) | Zero or variable curvature depending on spacetime |
| Key Structures | Hyperbolic planes, hyperboloids | Minkowski space, Lorentz manifolds |
| Fundamental Equation | Hyperbolic Laplacian (DH) | Lorentzian metric tensor (gmn) |
Introduction to Hyperbolic and Lorentzian Geometries
Hyperbolic geometry, characterized by a constant negative curvature, contrasts with Lorentzian geometry, which incorporates a metric of signature (-+++), essential in describing spacetime in general relativity. Hyperbolic spaces exhibit unique properties such as exponential growth of area with radius, while Lorentzian manifolds model causal structures and time-orientability in physics. Understanding these geometries provides critical insights into the behavior of curved spaces and the fundamental framework of the universe.
Mathematical Foundations of Hyperbolic Space
Hyperbolic space is modeled using a negative constant curvature metric, often represented by the hyperboloid model within Lorentzian manifolds. The Lorentzian metric, with signature (-,+,+,...), provides the mathematical foundation for hyperbolic geometry by defining distance and angle measures in a way that differs fundamentally from Euclidean space. This metric structure enables the rigorous study of hyperbolic geodesics, curvature, and isometries, establishing connections between hyperbolic and Lorentzian geometries in mathematical physics and differential geometry.
Key Properties of Lorentzian Geometry
Lorentzian geometry fundamentally differs from hyperbolic geometry by its metric signature of (-+++), enabling the modeling of spacetime in general relativity through time-like, space-like, and null intervals. Key properties of Lorentzian geometry include a causal structure defined by light cones, which distinguish events based on their potential causal relationships, and the existence of a non-degenerate, symmetric bilinear form that is not positive-definite. Unlike hyperbolic geometry's constant negative curvature, Lorentzian manifolds can have variable curvature dictated by Einstein's field equations, reflecting gravitational effects in a dynamic spacetime fabric.
Dimensional Differences and Structures
Hyperbolic geometry occurs in spaces with constant negative curvature, typically modeled in two or more dimensions using a hyperbolic metric that expands distances exponentially. Lorentzian geometry, fundamental in the theory of relativity, involves a metric with one time-like dimension and multiple space-like dimensions, defining a manifold with signature (-,+,+,+) for four-dimensional spacetime. While hyperbolic spaces emphasize curvature and distance relations in purely spatial dimensions, Lorentzian manifolds incorporate time as a key dimension, shaping causal structure and light-cone behavior distinct from hyperbolic metrics.
Metric Signatures: Hyperbolic vs Lorentzian
Hyperbolic geometry is characterized by a metric signature with all positive signs or all negative signs, commonly represented as ( + + ... + ) or ( - - ... - ), indicating a purely spatial structure without time-like dimensions. Lorentzian geometry employs a metric signature of the form ( - + + ... + ) or ( + - - ... - ), incorporating one time-like dimension alongside spatial dimensions, essential in the theory of relativity for modeling spacetime. The distinction in metric signatures fundamentally influences curvature properties, with hyperbolic spaces exhibiting constant negative curvature and Lorentzian manifolds allowing for the causal structure critical to relativistic physics.
Applications in Physics and Cosmology
Hyperbolic geometry models spacetime with constant negative curvature, playing a crucial role in theories of the universe's large-scale structure and in descriptions of accelerated expansion within cosmology. Lorentzian geometry underpins the mathematical framework of general relativity, characterizing spacetime with a metric signature that allows the distinction between time-like, space-like, and null intervals critical for understanding gravitational phenomena and black hole dynamics. Both geometries contribute to modern physics by providing essential tools for modeling diverse relativistic and cosmological scenarios, where hyperbolic spaces inform negative curvature effects and Lorentzian manifolds describe causal structure and time evolution.
Geodesics and Distance Calculations
Hyperbolic geometry features geodesics as curves minimizing distance in a space of constant negative curvature, where distance calculations involve hyperbolic trigonometric functions reflecting exponential growth. Lorentzian geometry, foundational in general relativity, uses geodesics representing paths of particles and light in a spacetime manifold with an indefinite metric signature, resulting in interval calculations based on the Minkowski metric. Differences in curvature and metric signature fundamentally impact the properties of geodesics and methods for measuring distances between points in these geometries.
Visualization and Model Representations
Hyperbolic geometry often utilizes the Poincare disk or hyperboloid models to visualize non-Euclidean spaces with constant negative curvature, emphasizing geodesics as arcs or curves within these models. Lorentzian geometry, central to the theory of relativity, employs Minkowski space representations that incorporate time-like and space-like intervals, visualized through light cones and worldlines to depict causality and spacetime structure. Visual models of hyperbolic spaces highlight infinite parallel lines and exponential growth of areas, whereas Lorentzian models focus on the metric signature (-+++), differentiating temporal and spatial dimensions for relativistic effects.
Transformations and Symmetry Groups
Hyperbolic geometry is governed by the hyperbolic group PSL(2, R), characterized by isometries preserving the hyperbolic metric and exhibiting non-Euclidean transformations like translations, rotations, and hyperbolic boosts. Lorentzian geometry, central in special relativity, involves the Lorentz group SO(1, n), with transformations preserving the Minkowski metric and encompassing rotations and Lorentz boosts that mix space and time coordinates. The fundamental difference lies in the metric signatures defining their symmetry groups: hyperbolic space relies on negative curvature with time-like and space-like separations, while Lorentzian manifolds emphasize invariant intervals under causal structure transformations.
Comparative Analysis: Strengths and Limitations
Hyperbolic geometry excels in modeling spaces with constant negative curvature, enabling efficient representations in network theory and complex data structures, whereas Lorentzian geometry underpins the mathematical framework of spacetime in general relativity, dealing with pseudo-Riemannian manifolds that combine time and space dimensions. Hyperbolic spaces provide strong tools for visualizing hierarchical and tree-like data but struggle with representing temporal phenomena, while Lorentzian manifolds effectively capture causal structures and time-oriented metrics but face challenges in purely spatial or purely hierarchical data representations. The choice between hyperbolic and Lorentzian geometries depends on the application's focus on spatial versus spatiotemporal modeling, balancing geometric intuitiveness and mathematical rigor.
Hyperbolic Infographic
 libterm.com
libterm.com