Primal space serves as the foundational setting in convex optimization where all variables are initially defined and constraints are applied. Understanding the geometry and structure of primal space is essential for solving optimization problems efficiently and accurately. Explore the rest of the article to deepen your grasp of primal space concepts and their practical applications.
Table of Comparison
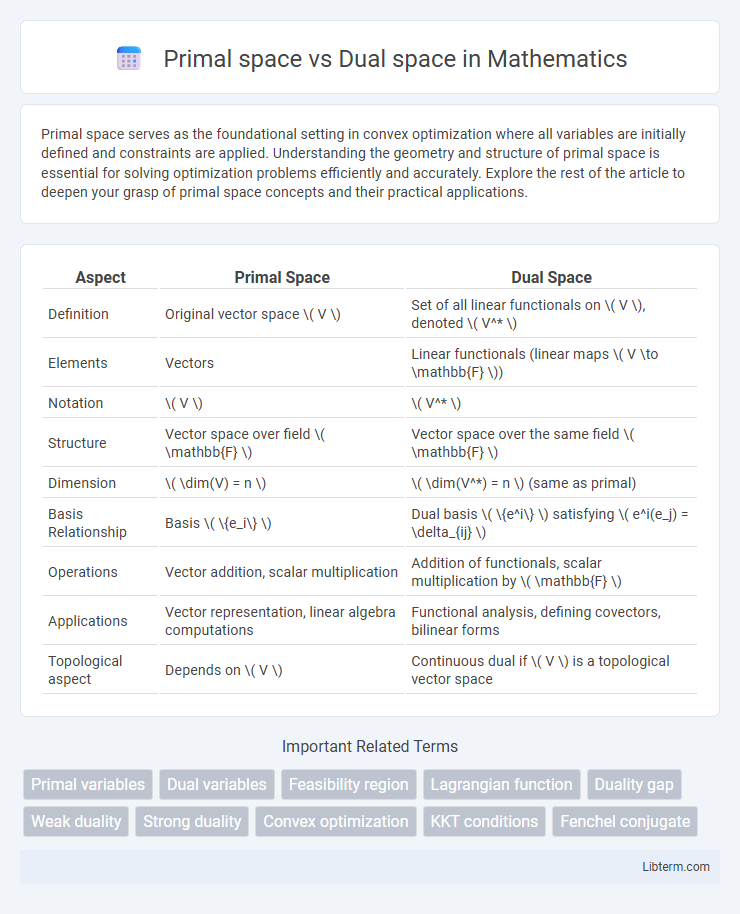
| Aspect | Primal Space | Dual Space |
|---|---|---|
| Definition | Original vector space \( V \) | Set of all linear functionals on \( V \), denoted \( V^* \) |
| Elements | Vectors | Linear functionals (linear maps \( V \to \mathbb{F} \)) |
| Notation | \( V \) | \( V^* \) |
| Structure | Vector space over field \( \mathbb{F} \) | Vector space over the same field \( \mathbb{F} \) |
| Dimension | \( \dim(V) = n \) | \( \dim(V^*) = n \) (same as primal) |
| Basis Relationship | Basis \( \{e_i\} \) | Dual basis \( \{e^i\} \) satisfying \( e^i(e_j) = \delta_{ij} \) |
| Operations | Vector addition, scalar multiplication | Addition of functionals, scalar multiplication by \( \mathbb{F} \) |
| Applications | Vector representation, linear algebra computations | Functional analysis, defining covectors, bilinear forms |
| Topological aspect | Depends on \( V \) | Continuous dual if \( V \) is a topological vector space |
Introduction to Primal and Dual Spaces
Primal space refers to the original vector space under consideration, where vectors are elements with specific algebraic structures. Dual space consists of all linear functionals mapping vectors from the primal space to the underlying field, typically real or complex numbers. Understanding the relationship between primal and dual spaces is fundamental in functional analysis, optimization, and linear algebra, as it facilitates the study of vector spaces through their linear mappings.
Fundamental Concepts: Vectors and Linear Functionals
Primal space consists of vectors, which are elements of a vector space characterized by operations of vector addition and scalar multiplication. Dual space is made up of linear functionals, which are linear maps from the primal space to its underlying field, assigning scalars to each vector. The fundamental relationship between these spaces is captured by the duality pairing, a bilinear form that evaluates a linear functional at a vector, establishing the connection between vectors and their corresponding linear functionals.
Mathematical Definitions: Primal vs Dual Space
The primal space in linear algebra refers to a vector space V over a field F, where vectors reside and linear operations are defined. The dual space V* consists of all linear functionals that map vectors from V to the field F, forming a vector space of linear maps. The dual space is mathematically defined as the set of all linear functionals f: V - F, providing a correspondence between each vector in the primal space and a scalar, crucial for understanding bidirectional mappings and functional analysis.
Geometric Interpretation of Primal and Dual Spaces
The primal space represents the original vector space where vectors are visualized as points or arrows, encapsulating directions and magnitudes in geometric form. The dual space consists of all linear functionals mapping vectors from the primal space to scalar values, interpreted geometrically as hyperplanes that evaluate or measure vectors in the primal space. The geometric interpretation links these spaces by viewing dual vectors as operators defining levels sets or contours in the primal vector space, illustrating a natural relationship between points (primal vectors) and hyperplanes (dual vectors).
Importance in Linear Algebra and Optimization
Primal space and dual space are fundamental concepts in linear algebra and optimization, representing vector spaces and their corresponding sets of linear functionals respectively. In optimization problems, the primal space encapsulates the original variables, while the dual space contains constraints and Lagrange multipliers, facilitating the analysis of optimality and sensitivity. Understanding the interplay between primal and dual spaces enables effective formulation of dual problems, strong duality conditions, and efficient algorithm design for convex optimization.
Basis Transformation: Primal and Dual Relationships
Basis transformation in primal space involves changing the coordinate system by applying an invertible matrix to the set of basis vectors, while in dual space, the transformation is characterized by applying the inverse transpose of that matrix to the dual basis vectors. The primal and dual bases satisfy the biorthogonality condition, ensuring that each functional in the dual basis extracts the corresponding coordinate from vectors in the primal basis. This framework facilitates seamless conversion between primal vectors and dual functionals, preserving linear structure and enabling efficient computations in linear algebra and functional analysis.
Key Differences Between Primal and Dual Spaces
Primal space refers to the original vector space where vectors and linear functions are defined, while dual space consists of all linear functionals mapping vectors from the primal space to the underlying field. Key differences include that the primal space contains vectors, and the dual space contains linear maps or covectors, with the dual space often having a different dimension only in infinite-dimensional settings. The dual space enables analysis of linear transformations and inner products through its correspondence with the primal space, highlighting its importance in fields like functional analysis and optimization.
Applications in Machine Learning and Data Science
Primal space and dual space concepts play a critical role in machine learning algorithms such as support vector machines (SVMs) where the primal space represents the original feature space, and the dual space enables the use of kernel functions to handle high-dimensional data efficiently. Optimization problems in linear and quadratic programming often leverage the dual formulation to achieve faster convergence and better scalability in training large datasets. Applications in data science include dimensionality reduction, feature selection, and designing robust predictive models by exploiting the relationships between primal-dual pairs for enhanced generalization and computational performance.
Examples Illustrating Primal and Dual Spaces
In linear algebra, the primal space typically refers to a vector space \(V\), such as \(\mathbb{R}^n\), where vectors represent points or directions, while the dual space \(V^*\) consists of all linear functionals mapping vectors from \(V\) to the underlying field, often \(\mathbb{R}\). For instance, in \(\mathbb{R}^3\), a vector \(\mathbf{v} = (v_1, v_2, v_3)\) belongs to the primal space, whereas a dual vector (covector) \(\mathbf{f}\) in the dual space might be defined as \(\mathbf{f}(\mathbf{v}) = a_1 v_1 + a_2 v_2 + a_3 v_3\), where \(a_i\) are scalars. This example illustrates how dual space elements act as linear maps taking vectors from the primal space and producing scalars, which is fundamental in fields like functional analysis and optimization.
Conclusion: Insights and Future Directions
Primal space and dual space concepts reveal fundamental relationships in optimization, highlighting how solutions in primal space correspond to constraints and variables in dual space, enabling more efficient problem-solving strategies. Insights from duality theory facilitate the development of advanced algorithms such as interior-point methods and support vector machines, which capitalize on these dual formulations for improved computational performance. Future research is expected to deepen understanding of non-convex dualities and explore their applications in machine learning, signal processing, and large-scale optimization problems.
Primal space Infographic
 libterm.com
libterm.com