Chaos often leads to unexpected opportunities and new perspectives that foster creativity and innovation. Embracing chaos can help you develop resilience and adaptability in both personal and professional life. Explore the rest of this article to discover how to harness the power of chaos for growth and success.
Table of Comparison
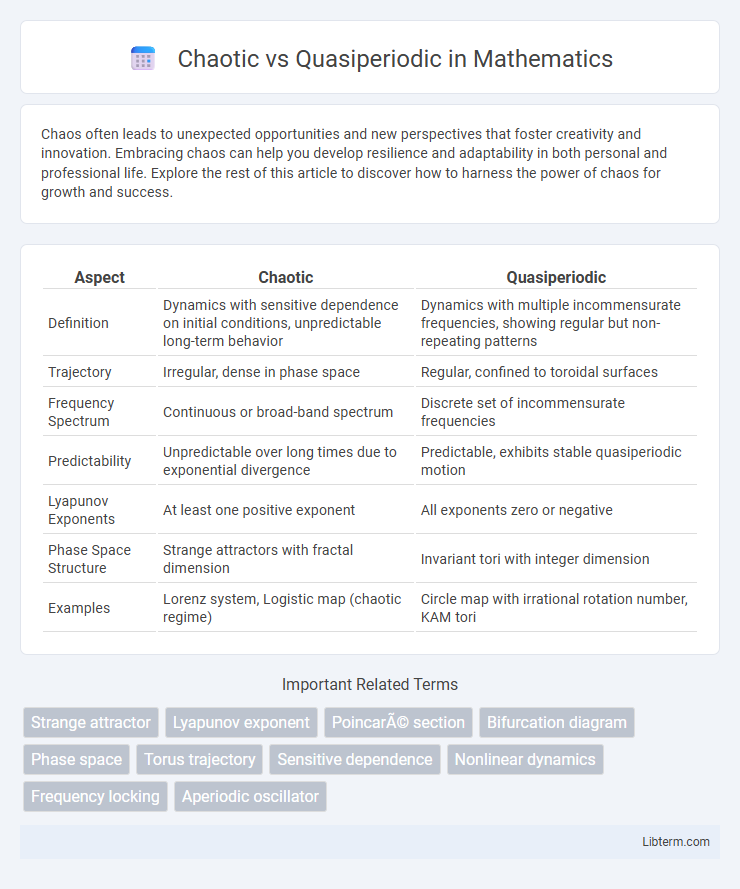
| Aspect | Chaotic | Quasiperiodic |
|---|---|---|
| Definition | Dynamics with sensitive dependence on initial conditions, unpredictable long-term behavior | Dynamics with multiple incommensurate frequencies, showing regular but non-repeating patterns |
| Trajectory | Irregular, dense in phase space | Regular, confined to toroidal surfaces |
| Frequency Spectrum | Continuous or broad-band spectrum | Discrete set of incommensurate frequencies |
| Predictability | Unpredictable over long times due to exponential divergence | Predictable, exhibits stable quasiperiodic motion |
| Lyapunov Exponents | At least one positive exponent | All exponents zero or negative |
| Phase Space Structure | Strange attractors with fractal dimension | Invariant tori with integer dimension |
| Examples | Lorenz system, Logistic map (chaotic regime) | Circle map with irrational rotation number, KAM tori |
Introduction to Chaotic and Quasiperiodic Systems
Chaotic systems exhibit sensitive dependence on initial conditions, leading to unpredictable and highly complex behavior over time, often characterized by strange attractors and fractal structures in phase space. Quasiperiodic systems, in contrast, display motion composed of two or more incommensurate frequencies, resulting in trajectories that densely fill tori in phase space without repeating exactly. Understanding the distinction between chaotic and quasiperiodic dynamics is crucial for analyzing nonlinear systems in fields such as physics, biology, and engineering.
Defining Chaos: Characteristics and Examples
Chaos is characterized by extreme sensitivity to initial conditions, deterministic unpredictability, and fractal structures in phase space, examples include weather systems and the double pendulum. Unlike quasiperiodic behavior, which features two or more incommensurate frequencies producing stable, non-repeating but predictable patterns, chaotic systems exhibit irregular, aperiodic trajectories. Key identifiers of chaos are strange attractors and positive Lyapunov exponents, quantifying the rate of divergence in system states over time.
Understanding Quasiperiodicity: Key Features
Quasiperiodicity is characterized by the superposition of two or more incommensurate frequencies, producing a non-repeating, yet structured pattern distinct from both periodic and chaotic behavior. Unlike chaos, quasiperiodic systems exhibit predictable trajectories on a torus-shaped phase space without sensitivity to initial conditions or exponential divergence. Key features include invariant tori, continuous frequency spectra with discrete peaks, and stability under small perturbations, making quasiperiodicity essential in areas such as celestial mechanics and nonlinear dynamics.
Mathematical Foundations: Equations and Models
Chaotic systems are governed by nonlinear differential equations such as the Lorenz system and logistic map, characterized by sensitive dependence on initial conditions and fractal attractors. Quasiperiodic behavior emerges from systems described by torus attractors and equations involving incommensurate frequencies, exemplified by the KAM (Kolmogorov-Arnold-Moser) theorem in Hamiltonian dynamics. Mathematical models for chaos use iterative maps and continuous-time dynamical systems, while quasiperiodicity relies on quasiperiodic functions and invariant tori to explain motion without exponential divergence.
Visualizing Behavior: Phase Space and Attractors
Chaotic systems exhibit sensitive dependence on initial conditions, producing strange attractors in phase space characterized by fractal structures and an aperiodic trajectory that never repeats. Quasiperiodic systems, in contrast, generate torus-shaped attractors with trajectories that densely fill the toroidal surface, showing multiple incommensurate frequencies without chaotic divergence. Visualizing these behaviors in phase space highlights the complexity of chaos through intricate, non-repeating patterns versus the smooth, nested loops of quasiperiodicity.
Real-World Applications: Where Chaos and Quasiperiodicity Occur
Chaos appears in weather systems, electrical circuits, and population dynamics, where unpredictable yet deterministic behavior affects forecasting and control. Quasiperiodicity arises in astrophysics, such as in the motion of celestial bodies and quasiperiodic crystals with unique structural properties used in material science. These phenomena influence fields from climate modeling to signal processing, highlighting the importance of understanding complex, non-repetitive patterns in real-world systems.
Distinguishing Chaos from Quasiperiodicity
Distinguishing chaos from quasiperiodicity involves analyzing the system's sensitivity to initial conditions and long-term predictability. Chaos exhibits exponential divergence of nearby trajectories and a positive Lyapunov exponent, while quasiperiodic systems display stable oscillations with incommensurate frequencies and zero Lyapunov exponent. Techniques such as phase space reconstruction and power spectral analysis help identify the irregular, aperiodic patterns of chaos versus the smooth, predictable frequency components of quasiperiodicity.
Methods for Analyzing System Dynamics
Methods for analyzing chaotic and quasiperiodic system dynamics include phase space reconstruction, Lyapunov exponents calculation, and frequency domain analysis. Phase space reconstruction visualizes trajectory patterns, distinguishing the irregularity of chaos from the structured cycles of quasiperiodicity. Lyapunov exponents quantify the rate of divergence in system states, with positive values indicating chaos, while spectral analysis identifies characteristic frequencies underpinning quasiperiodic oscillations.
Impacts on Prediction and Control
Chaotic systems exhibit sensitive dependence on initial conditions, leading to exponential divergence of trajectories and severe limitations in long-term prediction accuracy. Quasiperiodic systems, characterized by incommensurate frequencies, maintain structured yet non-repeating patterns, allowing for more reliable medium-term forecasting. Control strategies for chaotic dynamics require adaptive approaches to stabilize unstable periodic orbits, whereas quasiperiodic systems benefit from frequency-based control methods to manipulate phase relationships effectively.
Future Directions in Chaos and Quasiperiodicity Research
Future directions in chaos and quasiperiodicity research center on leveraging machine learning algorithms to identify hidden patterns and predict system behaviors in complex nonlinear systems. Advances in high-dimensional data analysis aim to deepen understanding of quasiperiodic attractors and their transition to chaos in physical and biological systems. Integration of experimental and computational methods promises to reveal novel applications ranging from secure communications to climate modeling by harnessing the interplay between chaotic dynamics and quasiperiodic structures.
Chaotic Infographic
 libterm.com
libterm.com