The fundamental group is a key concept in algebraic topology that captures the notion of loops in a topological space, revealing its essential shape characteristics. It assigns to each space a group consisting of equivalence classes of loops based at a point, providing a powerful tool for distinguishing spaces up to continuous deformation. Explore the rest of this article to deepen your understanding of how the fundamental group shapes the study of topology.
Table of Comparison
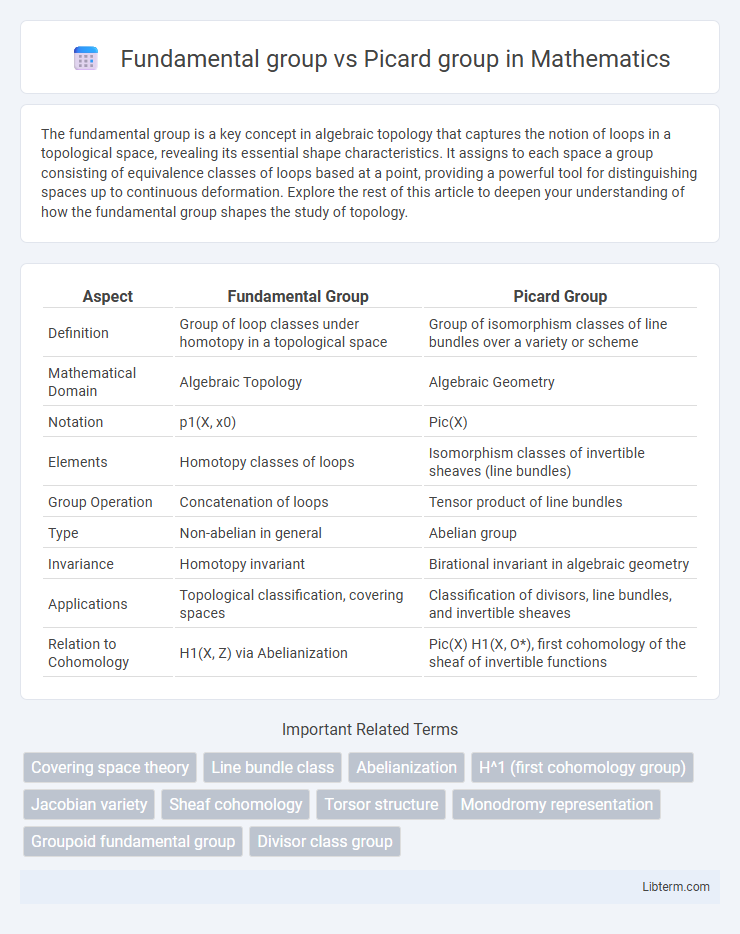
| Aspect | Fundamental Group | Picard Group |
|---|---|---|
| Definition | Group of loop classes under homotopy in a topological space | Group of isomorphism classes of line bundles over a variety or scheme |
| Mathematical Domain | Algebraic Topology | Algebraic Geometry |
| Notation | p1(X, x0) | Pic(X) |
| Elements | Homotopy classes of loops | Isomorphism classes of invertible sheaves (line bundles) |
| Group Operation | Concatenation of loops | Tensor product of line bundles |
| Type | Non-abelian in general | Abelian group |
| Invariance | Homotopy invariant | Birational invariant in algebraic geometry |
| Applications | Topological classification, covering spaces | Classification of divisors, line bundles, and invertible sheaves |
| Relation to Cohomology | H1(X, Z) via Abelianization | Pic(X) H1(X, O*), first cohomology of the sheaf of invertible functions |
Introduction to Fundamental Group and Picard Group
The fundamental group, denoted p1(X), captures the topological structure of a space X by classifying loops based at a point up to continuous deformation, revealing essential properties like connectedness and the presence of holes. The Picard group, Pic(X), arises in algebraic geometry and classifies isomorphism classes of line bundles or invertible sheaves on a variety X, encoding information about divisors and their linear equivalence. While the fundamental group is a homotopy-invariant topological tool, the Picard group reflects the algebraic and geometric structure of varieties, linking topology, sheaf theory, and divisor theory.
Basic Definitions: Fundamental Group
The fundamental group, denoted p1(X, x0), is the set of equivalence classes of loops based at a point x0 in a topological space X, with the group operation defined by loop concatenation. It captures the topological property of path-connectedness and encodes information about the space's holes and loops, providing a powerful invariant in algebraic topology. The fundamental group is a first homotopy group, reflecting the space's global shape and helping classify covering spaces.
Understanding the Picard Group
The Picard group classifies line bundles on a variety, encoding geometric and topological information through invertible sheaves, contrasting with the fundamental group which captures loop-based topological properties. Understanding the Picard group involves analyzing divisor classes and line bundle isomorphisms that reflect algebraic cycles and linear equivalence. This group plays a crucial role in algebraic geometry by linking cohomological data to geometric structures, particularly in describing the variety's moduli and deformation theory.
Algebraic and Topological Perspectives
The fundamental group captures the topological properties of a space by classifying its loops up to homotopy, serving as a key invariant in algebraic topology. In contrast, the Picard group arises in algebraic geometry, describing isomorphism classes of line bundles or divisor classes, thus encoding the algebraic structure of invertible sheaves on a variety. While the fundamental group reflects global topological connectivity, the Picard group provides deep insights into the variety's algebraic line bundles and their equivalence relations.
Fundamental Group: Key Properties and Examples
The fundamental group captures topological information by classifying loops in a space based on homotopy equivalence, serving as a crucial invariant in algebraic topology. Its key properties include being a topological invariant, having a group structure based on loop concatenation, and often reflecting the space's shape, such as p1(S^1) being isomorphic to the integers Z. Examples of fundamental groups include trivial groups for simply connected spaces like spheres S^n (n > 1) and free groups for wedge sums of circles, highlighting its role in distinguishing between different topological spaces.
Picard Group: Key Properties and Examples
The Picard group, denoted Pic(X), classifies isomorphism classes of line bundles on a variety or scheme X, serving as a crucial invariant in algebraic geometry. It encodes information about the divisor class group and the invertible sheaves, often providing insight into the geometric and arithmetic structure of X. Examples include the Picard group of a smooth projective curve, which is isomorphic to its Jacobian variety, and the Picard group of a projective space, isomorphic to the integers, generated by the class of the hyperplane bundle.
Connections and Differences Between Fundamental and Picard Groups
The fundamental group classifies loop-based topological structures of a space, capturing its homotopy classes of paths, while the Picard group classifies isomorphism classes of line bundles or invertible sheaves on algebraic varieties or complex manifolds, reflecting divisor and cohomology information. Both groups encode essential geometric and topological invariants but operate in distinct categorical frameworks: the fundamental group arises in algebraic topology, and the Picard group in algebraic geometry. Connections appear in the study of complex algebraic varieties where the fundamental group influences the structure of line bundles and the Picard group, especially through the first Chern class homomorphism relating line bundles to cohomology classes.
Applications in Algebraic Geometry
The fundamental group captures the topological structure of algebraic varieties by classifying their covering spaces, playing a crucial role in understanding monodromy and deformation theory. The Picard group, consisting of isomorphism classes of line bundles, is instrumental in studying divisors, linear systems, and the classification of algebraic varieties through their cohomological properties. Applications in algebraic geometry frequently involve using the fundamental group to analyze fiber bundles and the Picard group to explore moduli spaces, ampleness criteria, and the existence of global sections.
Importance in Topology and Classification Problems
The fundamental group captures essential information about the shape and connectivity of a topological space by classifying loops up to homotopy, making it a crucial tool in algebraic topology for distinguishing non-homeomorphic spaces. The Picard group, consisting of isomorphism classes of line bundles or invertible sheaves, plays a significant role in classifying complex varieties and algebraic surfaces by encoding geometric and arithmetic data. Both groups serve as powerful invariants in classification problems, with the fundamental group providing insight into homotopy types while the Picard group influences the study of divisors, line bundles, and deformation theory.
Conclusion: Comparative Insights
The fundamental group captures the topological properties of a space by classifying its loops up to homotopy, providing insights into its connectivity and covering spaces. The Picard group, on the other hand, classifies line bundles or divisors on algebraic varieties, reflecting geometric and algebraic structures related to invertible sheaves. Comparing both reveals that while the fundamental group is intrinsic to the space's topology, the Picard group encodes information about its line bundle geometry, making them complementary tools in algebraic geometry and topology.
Fundamental group Infographic
 libterm.com
libterm.com