Ordered data structures improve the efficiency of searching and sorting algorithms by maintaining elements in a specific sequence. This organization enhances your ability to quickly locate, insert, or delete items compared to unordered collections. Explore the rest of this article to understand how ordered structures can optimize your data management strategies.
Table of Comparison
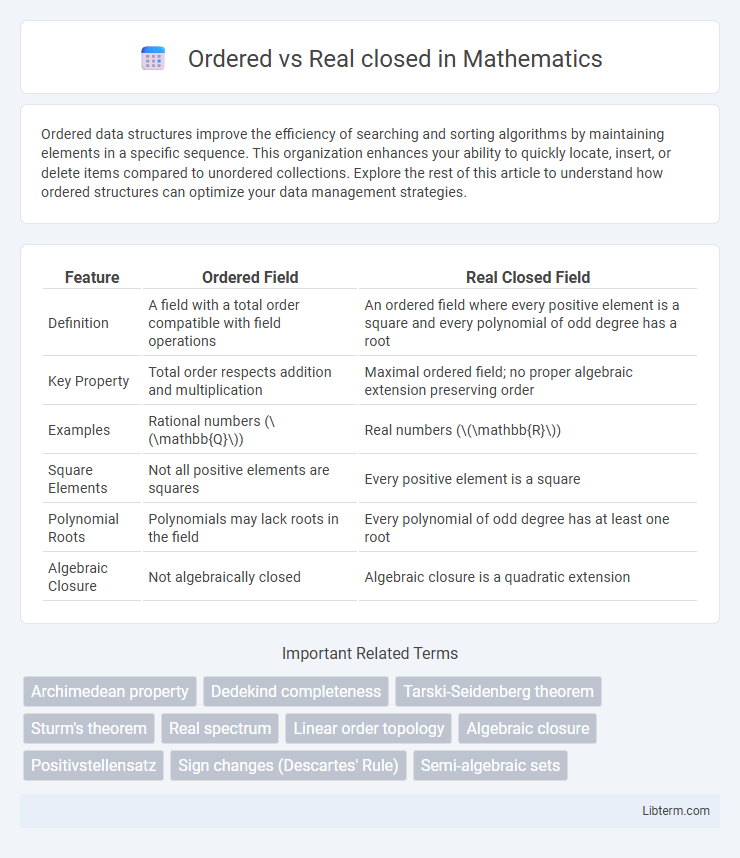
| Feature | Ordered Field | Real Closed Field |
|---|---|---|
| Definition | A field with a total order compatible with field operations | An ordered field where every positive element is a square and every polynomial of odd degree has a root |
| Key Property | Total order respects addition and multiplication | Maximal ordered field; no proper algebraic extension preserving order |
| Examples | Rational numbers (\(\mathbb{Q}\)) | Real numbers (\(\mathbb{R}\)) |
| Square Elements | Not all positive elements are squares | Every positive element is a square |
| Polynomial Roots | Polynomials may lack roots in the field | Every polynomial of odd degree has at least one root |
| Algebraic Closure | Not algebraically closed | Algebraic closure is a quadratic extension |
Introduction: Ordered Fields vs Real Closed Fields
Ordered fields are algebraic structures equipped with a total order compatible with field operations, ensuring positivity is well-defined and preserved under addition and multiplication. Real closed fields extend ordered fields by satisfying intermediate value properties analogous to the real numbers, including every positive element having a square root and every polynomial of odd degree having a root. The distinction lies in real closed fields being maximal ordered fields where no proper algebraic extension preserves the ordering, enabling a deeper connection to real algebraic geometry and model theory.
Definitions: What is an Ordered Field?
An ordered field is a field equipped with a total order compatible with the field operations, meaning the order respects addition and multiplication. This structure allows comparison of any two elements while preserving algebraic properties, ensuring if a <= b then a + c <= b + c and if 0 <= a and 0 <= b, then 0 <= a*b. Ordered fields serve as foundational frameworks for real number systems and analysis, supporting notions of positivity and order-based continuity.
Definitions: What is a Real Closed Field?
A real closed field is an ordered field that lacks any proper algebraic extension maintaining the order, meaning it is maximal with respect to its order-compatible algebraic extensions. It possesses the intermediate value property for polynomials, ensuring every positive element has a square root and every polynomial of odd degree has a root within the field. This contrasts with general ordered fields, which may lack such completeness properties and roots for all odd degree polynomials.
Key Properties of Ordered Fields
Ordered fields possess a total order compatible with field operations, ensuring that for any elements a and b, either a <= b or b <= a holds, and that addition and multiplication preserve order. These fields are formally equipped to handle inequalities, supporting a positive cone that defines the notion of positivity within the field. In contrast, real closed fields extend ordered fields by guaranteeing that every polynomial of odd degree has a root and enabling intermediate value properties, making them vital in real algebraic geometry.
Key Properties of Real Closed Fields
Real closed fields extend ordered fields by satisfying the intermediate value property for polynomials and ensuring every positive element has a square root, alongside the property that every polynomial of odd degree has a root within the field. These fields are formally real and admit a unique ordering compatible with their algebraic structure. Real closed fields serve as the algebraic closure of ordered fields under the ordering constraints, exemplified by the field of real numbers.
Examples: Ordered Fields in Practice
Ordered fields such as the rational numbers (\(\mathbb{Q}\)) provide a foundational example where addition, multiplication, and a total order coexist, enabling basic arithmetic and inequalities in algebra. Real closed fields, like the real numbers (\(\mathbb{R}\)), extend this structure with properties ensuring that every positive element is a square and every polynomial of odd degree has a root, supporting advanced calculus and real algebraic geometry. These distinctions highlight practical applications: ordered fields model rational approximations, while real closed fields underpin continuous phenomena and solution existence in real-world problems.
Examples: Real Closed Fields in Mathematics
Real closed fields, such as the field of real numbers \(\mathbb{R}\), are ordered fields where every positive element has a square root and every polynomial of odd degree has at least one root. Another example includes the field of real algebraic numbers, which is the real closure of the rational numbers \(\mathbb{Q}\). In contrast, ordered fields like the rational numbers \(\mathbb{Q}\) lack completeness and do not satisfy these root properties, illustrating key differences between ordered and real closed fields.
Major Differences: Ordered vs Real Closed
Ordered fields are algebraic structures where every element is comparable with a total order compatible with addition and multiplication, while real closed fields extend ordered fields by guaranteeing that every positive element has a square root and every polynomial of odd degree has a root. A key difference lies in real closed fields being algebraically closed within the class of ordered fields, meaning they cannot be properly extended without losing the order property. Real closed fields provide the foundation for real algebraic geometry and allow for solving polynomial equations fully ordered by their roots, unlike generic ordered fields.
Applications in Algebra and Analysis
Ordered fields provide a framework for algebraic structures where inequalities are well-defined, enabling the study of polynomial inequalities and real algebraic geometry. Real closed fields extend ordered fields by satisfying the intermediate value property, making them essential in model theory and decision problems within real algebraic geometry. Applications in analysis include using real closed fields to generalize properties of the real numbers, facilitating solutions to equations that are not tractable in arbitrary ordered fields.
Summary: Choosing Between Ordered and Real Closed Fields
Ordered fields provide a structure where elements maintain a total order compatible with field operations, essential for real analysis and constructive proofs. Real closed fields extend ordered fields by ensuring every positive element has a square root and every polynomial of odd degree has a root, enabling algebraic closure properties without losing order. Selecting between ordered and real closed fields depends on the need for solving polynomial equations algebraically while preserving an order structure, with real closed fields offering a more robust framework for advanced algebraic and geometric applications.
Ordered Infographic
 libterm.com
libterm.com