A torsion-free module is an algebraic structure where multiplying any nonzero element by a nonzero scalar never results in zero, ensuring the absence of elements with finite order. This property plays a crucial role in module theory and algebraic geometry, allowing for better structural analysis and classification of modules over integral domains. Explore this article to deepen your understanding of torsion-free modules and their significance in advanced mathematics.
Table of Comparison
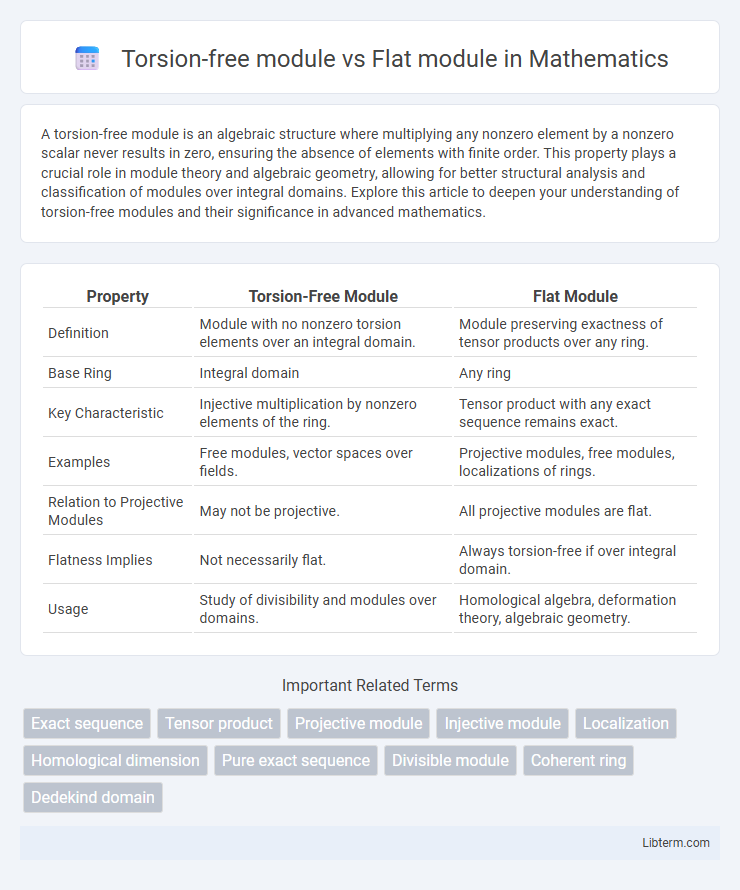
| Property | Torsion-Free Module | Flat Module |
|---|---|---|
| Definition | Module with no nonzero torsion elements over an integral domain. | Module preserving exactness of tensor products over any ring. |
| Base Ring | Integral domain | Any ring |
| Key Characteristic | Injective multiplication by nonzero elements of the ring. | Tensor product with any exact sequence remains exact. |
| Examples | Free modules, vector spaces over fields. | Projective modules, free modules, localizations of rings. |
| Relation to Projective Modules | May not be projective. | All projective modules are flat. |
| Flatness Implies | Not necessarily flat. | Always torsion-free if over integral domain. |
| Usage | Study of divisibility and modules over domains. | Homological algebra, deformation theory, algebraic geometry. |
Introduction to Torsion-Free and Flat Modules
Torsion-free modules are modules over a ring R in which no nonzero element is annihilated by a nonzero element of R, ensuring a stronger form of linear independence within the module. Flat modules are defined by the preservation of exact sequences under the tensor product, making them essential in homological algebra and algebraic geometry. Understanding torsion-free and flat modules clarifies their roles in module theory, with torsion-free modules emphasizing element-wise divisibility properties and flat modules ensuring exactness properties under base change.
Defining Torsion-Free Modules
Torsion-free modules over an integral domain are modules in which no nonzero element is annihilated by a nonzero element of the domain, ensuring the absence of torsion elements. Flat modules are characterized by the property that tensoring with them preserves exact sequences, making them a broader class that includes all torsion-free modules but can also contain modules with torsion. The distinction lies in torsion-free modules emphasizing the internal structure related to the domain's zero divisors, while flat modules emphasize the behavior of the module under tensor operations.
Defining Flat Modules
Flat modules are defined by their ability to preserve exact sequences under the tensor product operation, ensuring that tensoring with a flat module maintains the exactness of any short exact sequence of modules. Unlike torsion-free modules, which primarily restrict the presence of elements annihilated by non-zero divisors, flat modules guarantee that the tensor functor is exact, making flatness a stronger and more algebraically robust property. This distinction highlights the importance of flat modules in homological algebra and module theory for retaining structural integrity during tensor product operations.
Key Properties of Torsion-Free Modules
Torsion-free modules over an integral domain ensure that no nonzero element is annihilated by a nonzero scalar, preserving injectivity in scalar multiplication. These modules embed naturally into their field of fractions, maintaining structural rigidity without introducing torsion elements. Unlike flat modules, which guarantee exactness under tensor products, torsion-free modules specifically exclude elements of finite order, highlighting their distinct algebraic purity.
Fundamental Properties of Flat Modules
Flat modules are characterized by the preservation of exact sequences under the tensor product functor, ensuring that tensoring with a flat module does not introduce torsion or distort module structure. Every flat module is torsion-free, but the converse does not hold; torsion-free modules may fail to maintain exactness when tensored. Fundamental properties of flat modules include closure under direct limits and extensions, making them essential in homological algebra and algebraic geometry for constructing and analyzing well-behaved module categories.
Relationships Between Torsion-Free and Flat Modules
Torsion-free modules over integral domains exhibit a strong connection to flat modules, as every flat module is torsion-free, but the converse does not always hold. In particular, over principal ideal domains (PIDs), torsion-free modules coincide with flat modules, illustrating their equivalence in these contexts. This relationship highlights the importance of ring structure in determining when torsion-freeness implies flatness, especially in algebraic and homological algebra settings.
Examples Illustrating Torsion-Free and Flat Modules
A torsion-free module over an integral domain, such as the module \(\mathbb{Z}\) over itself, contains no elements annihilated by nonzero ring elements, exemplified by \(\mathbb{Z}^n\) being torsion-free but not necessarily flat. Flat modules include free modules like \(\mathbb{Q}\) over \(\mathbb{Z}\), which are torsion-free and preserve exact sequences under tensoring. The \(\mathbb{Z}\)-module \(\mathbb{Q}/\mathbb{Z}\) is neither torsion-free nor flat, illustrating that torsion-freeness and flatness are distinct properties with some overlap.
Major Differences: Torsion-Free vs Flat
Torsion-free modules over an integral domain contain no nonzero elements annihilated by nonzero scalars, emphasizing the absence of torsion elements. Flat modules preserve exact sequences under tensor products, ensuring exactness is maintained when tensoring with any module. The major difference lies in torsion-free modules focusing on non-annihilation properties, while flat modules are characterized by exactness preservation in tensor operations.
Applications in Algebra and Module Theory
Torsion-free modules are fundamental in algebra for studying modules over integral domains, ensuring elements are not annihilated by nonzero scalars and facilitating the analysis of divisibility properties. Flat modules play a crucial role in homological algebra and algebraic geometry by preserving exact sequences under tensor products, which is essential for understanding base change, localization, and deformation theory. Both torsion-free and flat modules enable deeper insights into module behavior, with torsion-free modules emphasizing structural integrity and flat modules supporting exactness conditions in module theory.
Summary and Comparative Insights
Torsion-free modules are modules over integral domains where no nonzero element is annihilated by a nonzero scalar, emphasizing the absence of torsion elements, while flat modules maintain exactness under tensor products, ensuring the preservation of exact sequences. All flat modules are torsion-free over integral domains, but the converse is not true, as torsion-free modules may fail to preserve exactness during tensoring. Flatness is a stronger condition related to the homological behavior and exactness properties, whereas torsion-freeness is a more straightforward structural property concerning element annihilation.
Torsion-free module Infographic
 libterm.com
libterm.com