The greatest lower bound, also known as the infimum, is the highest value that is less than or equal to every element in a given set. It plays a crucial role in mathematical analysis and optimization by providing the most accurate measure of the lowest achievable limit within a range. Discover how understanding the greatest lower bound can enhance your mathematical reasoning in the rest of this article.
Table of Comparison
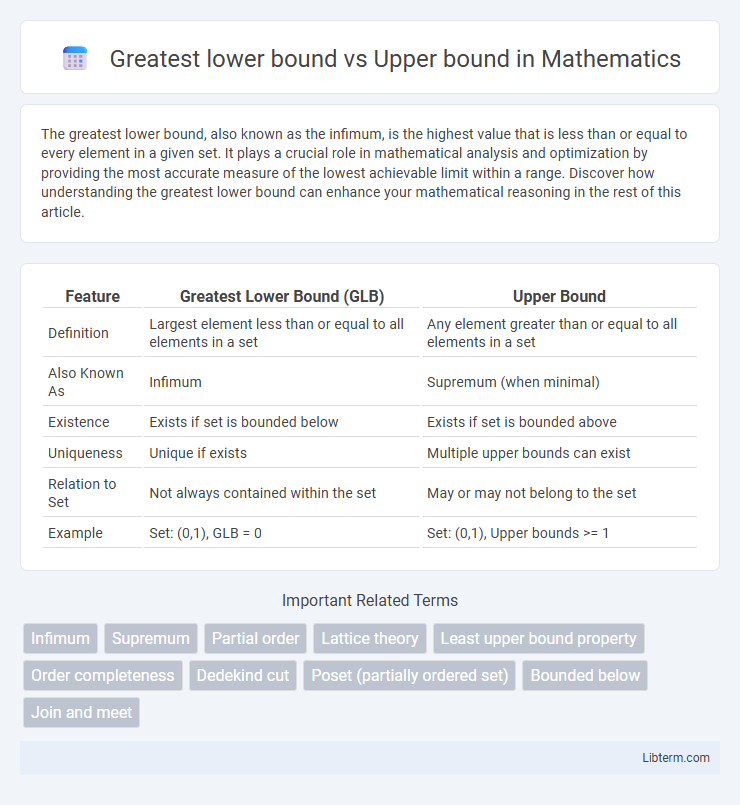
| Feature | Greatest Lower Bound (GLB) | Upper Bound |
|---|---|---|
| Definition | Largest element less than or equal to all elements in a set | Any element greater than or equal to all elements in a set |
| Also Known As | Infimum | Supremum (when minimal) |
| Existence | Exists if set is bounded below | Exists if set is bounded above |
| Uniqueness | Unique if exists | Multiple upper bounds can exist |
| Relation to Set | Not always contained within the set | May or may not belong to the set |
| Example | Set: (0,1), GLB = 0 | Set: (0,1), Upper bounds >= 1 |
Understanding Greatest Lower Bound and Upper Bound
The greatest lower bound (GLB), also known as the infimum, is the highest value that is less than or equal to every element in a given set, serving as the most precise lower limit. The upper bound is any value that is greater than or equal to every element in the set, providing an upper limit that contains the set within its boundary. Understanding the difference involves recognizing that the greatest lower bound is the largest among all possible lower bounds, ensuring the set does not have any lower bound greater than it, whereas an upper bound may not be the least upper limit unless specified as the supremum.
Definitions: What Is a Lower Bound?
A lower bound of a set in mathematics is a value that is less than or equal to every element within that set, serving as a minimum limit that no elements fall below. In ordered sets, the greatest lower bound, or infimum, is the highest value among all lower bounds, providing the closest boundary not exceeded by the set elements. Upper bounds contrast by being values greater than or equal to every set element, with the least upper bound or supremum as the smallest such value that still bounds the set from above.
Definitions: What Is an Upper Bound?
An upper bound of a set in a partially ordered set is an element greater than or equal to every element of that set. The concept is crucial in analysis and order theory for defining limits and bounds within ordered structures. Unlike the greatest lower bound, which is the maximal element less than or equal to all elements, the upper bound need not be unique or minimal.
Differences Between Lower Bound and Upper Bound
Greatest lower bound (GLB) is the highest value that is less than or equal to all elements in a set, while the upper bound is any value greater than or equal to all elements within the set. The GLB, also known as the infimum, is the maximal element among all lower bounds, whereas the minimal element among all upper bounds is called the least upper bound or supremum. Unlike upper bounds, which can be multiple and not necessarily minimal, the greatest lower bound is uniquely defined when it exists.
Mathematical Notation and Representation
The greatest lower bound (glb), denoted as \( \inf S \), represents the highest value that is less than or equal to every element in a set \( S \subseteq \mathbb{R} \), while the upper bound, denoted as \( \sup S \), is the smallest value greater than or equal to every element in \( S \). Formally, \( m = \inf S \) satisfies \( m \leq s \) for all \( s \in S \) and for any \( \varepsilon > 0 \), there exists \( s \in S \) such that \( s < m + \varepsilon \), whereas \( M = \sup S \) satisfies \( M \geq s \) for all \( s \in S \) and for any \( \varepsilon > 0 \), there exists \( s \in S \) such that \( s > M - \varepsilon \). Both bounds serve as critical concepts in analysis and order theory and are expressed through inequalities and limit conditions related to the elements of \( S \).
Real-World Applications of Bounds
Greatest lower bound (infimum) and upper bound (supremum) play crucial roles in optimization problems, such as determining the minimum resource allocation or maximum allowable stress in engineering designs. In economics, these bounds help define price floors and ceilings to stabilize markets and prevent extreme fluctuations. Signal processing relies on bounds to ensure error rates stay within acceptable limits, enhancing communication reliability and system performance.
Greatest Lower Bound (Infimum) Explained
The Greatest Lower Bound, or Infimum, refers to the highest value that is less than or equal to every element in a subset of a partially ordered set, ensuring no larger lower bound exists. It plays a crucial role in analysis and order theory by providing a precise limit from below, even if the set lacks a minimum element. This concept underpins the completeness property of real numbers and is fundamental in defining integrals, limits, and bounds in mathematical optimization.
Least Upper Bound (Supremum) Explained
The least upper bound, or supremum, of a set is the smallest value that is greater than or equal to every element in that set, ensuring no smaller upper bound exists. It is a crucial concept in real analysis, particularly in the study of bounded sets and their limits. Understanding the supremum helps determine the precise boundary values and supports proofs involving convergence and completeness in ordered sets.
Visualizing Bounds on the Number Line
Greatest lower bound (infimum) and upper bound (supremum) can be visualized on a number line by identifying the smallest value that is greater than or equal to every element of a set and the largest value that is less than or equal to every element of a set, respectively. The greatest lower bound marks the furthest point to the right that still lies below all points in the set, while the upper bound is the furthest left point that is above all points in the set. Visualizing these bounds helps clarify containment and limit concepts, especially when sets are intervals or collections of real numbers.
Importance of Bounds in Mathematical Analysis
Greatest lower bound (infimum) and upper bound (supremum) are critical in mathematical analysis for defining the exact limits of sets and functions within ordered structures. They ensure precision in characterizing convergence, continuity, and optimization problems by bounding values tightly from below and above. The concept of bounds underpins the rigorous development of calculus and real analysis, facilitating error estimation and the formulation of well-defined limits.
Greatest lower bound Infographic
 libterm.com
libterm.com