K-theory spectrum captures intricate algebraic and topological properties through stable homotopy types, offering deep insights into vector bundles and generalized cohomology theories. Researchers use it to study the classification of complex structures and probe stable phenomena in algebraic topology. Explore the full article to understand how the K-theory spectrum shapes modern mathematical frameworks and applications.
Table of Comparison
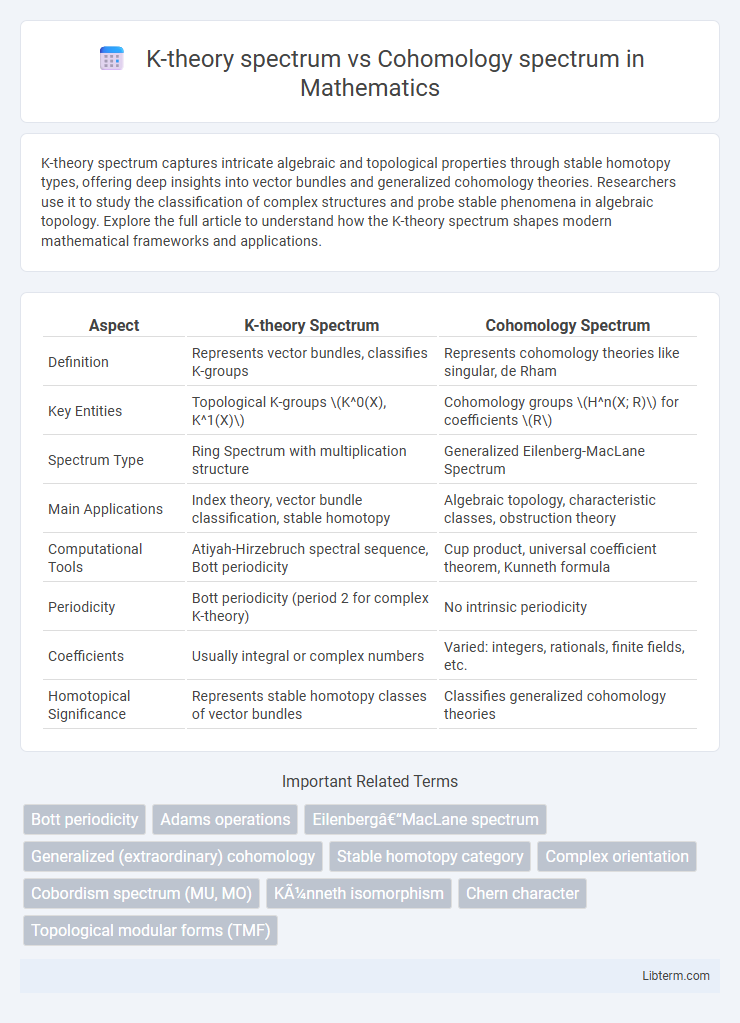
| Aspect | K-theory Spectrum | Cohomology Spectrum |
|---|---|---|
| Definition | Represents vector bundles, classifies K-groups | Represents cohomology theories like singular, de Rham |
| Key Entities | Topological K-groups \(K^0(X), K^1(X)\) | Cohomology groups \(H^n(X; R)\) for coefficients \(R\) |
| Spectrum Type | Ring Spectrum with multiplication structure | Generalized Eilenberg-MacLane Spectrum |
| Main Applications | Index theory, vector bundle classification, stable homotopy | Algebraic topology, characteristic classes, obstruction theory |
| Computational Tools | Atiyah-Hirzebruch spectral sequence, Bott periodicity | Cup product, universal coefficient theorem, Kunneth formula |
| Periodicity | Bott periodicity (period 2 for complex K-theory) | No intrinsic periodicity |
| Coefficients | Usually integral or complex numbers | Varied: integers, rationals, finite fields, etc. |
| Homotopical Significance | Represents stable homotopy classes of vector bundles | Classifies generalized cohomology theories |
Introduction to K-Theory and Cohomology Spectra
K-theory spectrum represents a foundational tool in algebraic topology capturing vector bundle information over topological spaces, encoding stable isomorphism classes via a spectrum constructed from classifying spaces of unitary groups. Cohomology spectra generalize classical cohomology theories by assigning a sequence of spaces whose homotopy groups define generalized cohomology theories, often arising from Eilenberg-MacLane spaces representing singular cohomology. The interplay between K-theory and cohomology spectra reveals deep structural insights, as K-theory spectra provide refined invariants that enrich the information obtained from ordinary cohomology spectra, establishing connections through spectral sequences and Chern character maps.
Historical Background and Motivations
The development of the K-theory spectrum originated in the 1950s with Alexander Grothendieck's introduction of K-groups to classify vector bundles, providing a homotopy-theoretic framework for algebraic topology and functional analysis. In contrast, the cohomology spectrum emerged from the classical cohomology theories, formalized through the Eilenberg-MacLane spaces to capture generalized cohomology theories in stable homotopy theory. Motivations for K-theory spectrum focused on understanding vector bundle classification and operator algebras, while cohomology spectra aimed to unify various cohomological invariants under a homotopical and categorical formalism.
Spectrum: Definition and Role in Algebraic Topology
The K-theory spectrum is a structured sequence of spaces representing complex vector bundles, providing a generalized cohomology theory capturing stable phenomena in algebraic topology. The cohomology spectrum, often associated with ordinary cohomology theories like singular or de Rham cohomology, encodes information about topological spaces through homotopy-invariant algebraic invariants. Both spectra serve as fundamental tools in stable homotopy theory, enabling computations of homotopy groups and facilitating the study of manifold invariants, index theorems, and characteristic classes.
Construction of the K-Theory Spectrum
The K-theory spectrum is constructed through a sequence of classifying spaces associated with exact categories or topological vector bundles, capturing stable homotopy-theoretic information about vector bundles. Unlike the cohomology spectrum, which is derived from generalized cohomology theories based on Eilenberg-MacLane spaces or complex orientations, the K-theory spectrum encodes algebraic and geometric properties of modules or bundles via infinite loop spaces and Quillen's Q-construction. This stable homotopy approach allows the K-theory spectrum to link algebraic geometry, operator algebras, and topological spaces through structured ring spectra and Bott periodicity phenomena.
Construction of the Cohomology Spectrum
The cohomology spectrum is constructed using Eilenberg-MacLane spaces that represent ordinary cohomology theories, forming an Omega-spectrum where each space corresponds to a specific cohomological dimension. In contrast, the K-theory spectrum arises from classifying spaces of vector bundles, capturing topological K-theory via Bott periodicity. This construction enables stable homotopy theoretic analysis of cohomology operations and facilitates comparison between generalized cohomology theories.
Key Differences between K-Theory and Cohomology Spectra
K-theory spectra classify vector bundles over a topological space, capturing information about stable equivalence classes of vector bundles and their tensor product structures, while cohomology spectra represent generalized cohomology theories derived from homotopy classes of maps into Eilenberg-MacLane spaces or other spectra. The K-theory spectrum is multiplicative and more refined, encoding richer algebraic structures such as ring spectra, whereas cohomology spectra typically reflect additive invariants and can be simpler to compute using cup products. Moreover, K-theory captures information related to bundle theory and index theorems, whereas cohomology spectra are oriented towards classifying characteristic classes and homotopy-invariant properties.
Applications in Stable Homotopy Theory
K-theory spectrum and cohomology spectrum serve as fundamental tools in stable homotopy theory, providing frameworks to analyze vector bundles and generalized cohomology theories respectively. The K-theory spectrum captures information about vector bundles and their classes, enabling computations of stable homotopy groups with connections to index theory and fixed point theorems. Cohomology spectra, such as Eilenberg-MacLane spectra, facilitate understanding of generalized cohomology theories, enabling the classification of stable homotopy types and detecting subtle invariants beyond ordinary cohomology.
Computational Aspects of K-Theory vs Cohomology
K-theory spectra facilitate computations involving vector bundles and stable homotopy classes, leveraging exact sequences and Bott periodicity to simplify calculations, particularly in topological contexts. Cohomology spectra provide algebraic invariants via Eilenberg-MacLane spaces, enabling straightforward chain-level computations and cup product structures that are amenable to spectral sequences such as the Atiyah-Hirzebruch spectral sequence. Computational challenges in K-theory often arise from handling complex vector bundle data and nontrivial differentials, whereas cohomology spectra benefit from more accessible algebraic frameworks and established computational tools in homological algebra.
Interactions and Generalizations in Modern Mathematics
K-theory spectrum and cohomology spectrum interact through their roles in generalized cohomology theories, providing deep insights into topological and algebraic structures. Their generalizations lead to structured ring spectra and equivariant cohomology theories, which unify various invariants via stable homotopy theory frameworks. These interactions facilitate advanced applications in areas such as index theory, motivic homotopy theory, and the study of characteristic classes.
Future Directions and Open Problems
Exploring the interplay between K-theory spectra and cohomology spectra reveals emerging challenges in understanding their computational complexity and potential unifying frameworks in stable homotopy theory. Future research targets refining the chromatic filtration and enhancing spectral sequence convergence to unravel deeper algebraic structures within these spectra. Addressing open problems involves developing novel categorical models and extending equivariant and motivic contexts to better capture the intricacies of generalized cohomology theories.
K-theory spectrum Infographic
 libterm.com
libterm.com