Optimizing your website for search engines involves strategic keyword placement, engaging content creation, and improving site performance to enhance visibility and user experience. Effective SEO practices also include quality backlink building and mobile-friendly design to boost your rankings. Explore the rest of this article to discover actionable tips for elevating your online presence.
Table of Comparison
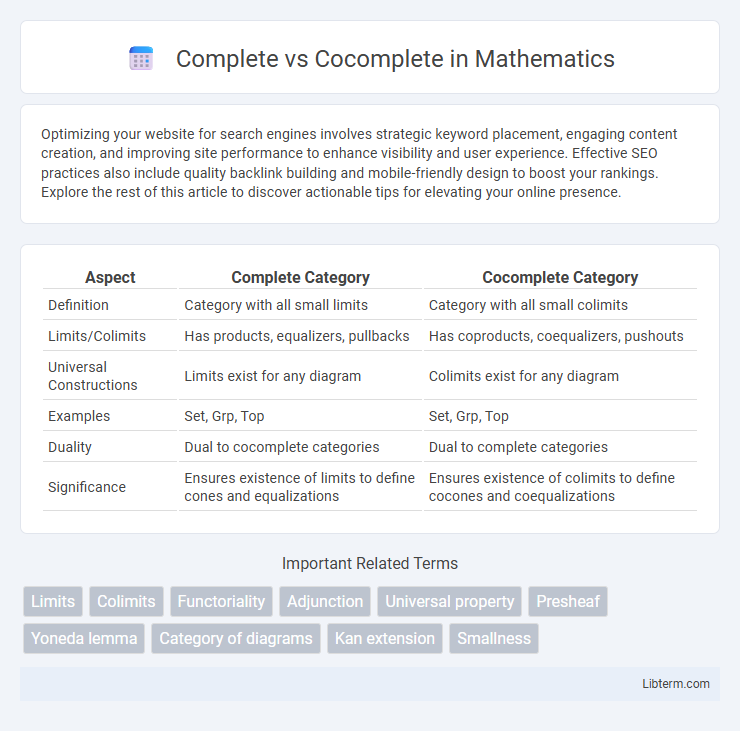
| Aspect | Complete Category | Cocomplete Category |
|---|---|---|
| Definition | Category with all small limits | Category with all small colimits |
| Limits/Colimits | Has products, equalizers, pullbacks | Has coproducts, coequalizers, pushouts |
| Universal Constructions | Limits exist for any diagram | Colimits exist for any diagram |
| Examples | Set, Grp, Top | Set, Grp, Top |
| Duality | Dual to cocomplete categories | Dual to complete categories |
| Significance | Ensures existence of limits to define cones and equalizations | Ensures existence of colimits to define cocones and coequalizations |
Understanding Completeness and Coccompleteness
Completeness in category theory indicates that a category has all small limits, enabling constructions like products and equalizers, while cocompleteness requires all small colimits, supporting coproducts and coequalizers. Understanding completeness allows mathematicians to work with structured data aggregations, whereas cocompleteness facilitates the combination and identification processes within categories. Categories such as Set and Vect are both complete and cocomplete, exemplifying their foundational role in algebra and topology.
Key Definitions: Complete and Cocomplete Categories
Complete categories have all small limits, including products, equalizers, and pullbacks, enabling the definition of universal cones. Cocomplete categories possess all small colimits, such as coproducts, coequalizers, and pushouts, facilitating the construction of universal cocones. Understanding these key distinctions is essential in category theory for analyzing the availability of limits and colimits within different categorical structures.
Limits: Foundations of Completeness
Complete categories contain all small limits, including products, equalizers, and pullbacks, providing a foundation for constructing universal cones. Cocomplete categories possess all small colimits such as coproducts, coequalizers, and pushouts, essential for universal co-cones. Understanding limits and colimits as fundamental concepts distinguishes completeness and cocompleteness in categorical structures.
Colimits: The Basis of Cocompleteness
Colimits serve as the foundational structure in cocomplete categories, where all small colimits exist by definition, enabling the construction of objects from diagrams via universal cocone properties. Complete categories contrast by focusing on limits, with completeness defined by the existence of all small limits, while cocompleteness emphasizes closure under colimits such as coproducts, coequalizers, and pushouts. Understanding colimits as the basis of cocompleteness clarifies how categories manage universal constructions that generalize operations like unions and quotient objects.
Practical Examples of Complete Categories
Complete categories possess all small limits, such as products and equalizers, enabling the construction of pullbacks and terminal objects in practical applications. For example, the category of sets is complete because it supports arbitrary products and equalizers, allowing the formation of subset intersections and function spaces. In contrast, cocomplete categories have all small colimits, including coproducts and coequalizers, essential for practical constructions like quotients and disjoint unions.
Real-World Cases of Cocomplete Categories
Cocomplete categories appear in real-world cases such as database schema design, where colimits represent the merging of datasets or views, facilitating query optimization and data integration. In programming, cocomplete categories model systems with universal constructions like pushouts, enabling the consistent combination of state spaces or type systems in software development. These applications highlight the practical importance of cocompleteness for ensuring the existence of all colimits necessary for unifying diverse structures in complex systems.
Comparing Complete and Cocomplete Structures
Complete structures feature all small limits, ensuring the existence of all pullbacks and products, while cocomplete structures have all small colimits, guaranteeing all pushouts and coproducts. In category theory, completeness allows for the construction of objects through limiting processes, whereas cocompleteness enables object formation via colimiting processes. Comparing these concepts highlights their duality, with completeness focusing on universal cones and cocompleteness on universal co-cones.
Importance in Category Theory
Complete categories possess all small limits, enabling the construction of products, equalizers, and pullbacks essential for defining universal properties in category theory. Cocomplete categories, characterized by having all small colimits, facilitate the formation of coproducts, coequalizers, and pushouts, crucial for constructing quotients and direct limits. The interplay between completeness and cocompleteness underpins the versatility of categorical constructions, supporting advanced concepts like adjoint functors and Kan extensions in mathematical and computational frameworks.
Applications in Mathematics and Computer Science
Complete categories, which have all small limits, are essential in mathematical contexts like topology and algebra for structuring objects with consistent universal properties, enabling constructions such as products, equalizers, and pullbacks. Cocomplete categories possess all small colimits, facilitating data aggregation, quotient structures, and free constructions, crucial in computer science for modeling state transitions, type theories, and functional programming semantics. Both concepts underpin domain theory and categorical logic, supporting fixed-point computations and recursive definitions fundamental to programming language semantics and formal verification.
Summary: Choosing Between Complete and Cocomplete
Complete categories feature all limits, enabling the construction of universal objects such as products and equalizers, essential in defining structured diagrams and preserving existing patterns. Cocomplete categories incorporate all colimits, facilitating the formation of co-products and coequalizers, important for extending structures and modeling processes involving sums and identifications. Choosing between complete and cocomplete depends on whether the focus is on preserving limit-based structures or enabling flexible constructions through colimits, often determined by the specific requirements of the mathematical framework or application domain.
Complete Infographic
 libterm.com
libterm.com