Betti cohomology provides a powerful tool for analyzing the topological properties of complex varieties through singular cohomology groups with rational coefficients. This approach links geometry and algebra, revealing important invariants such as Betti numbers that classify spaces based on their holes and cycles. Explore the rest of the article to deepen your understanding of how Betti cohomology impacts modern mathematical research.
Table of Comparison
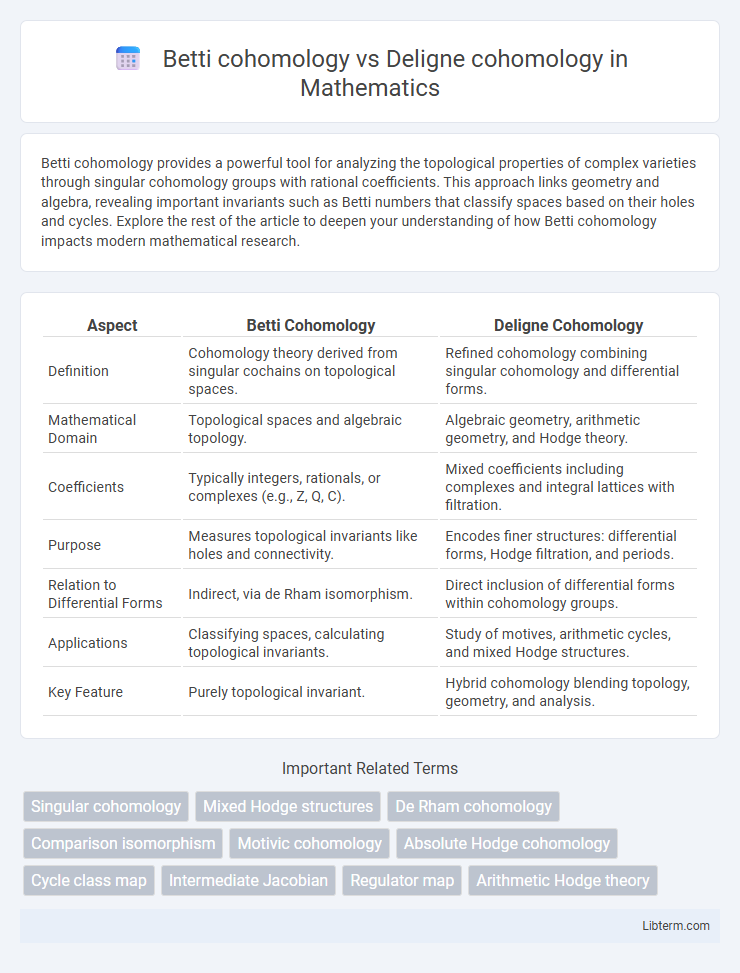
| Aspect | Betti Cohomology | Deligne Cohomology |
|---|---|---|
| Definition | Cohomology theory derived from singular cochains on topological spaces. | Refined cohomology combining singular cohomology and differential forms. |
| Mathematical Domain | Topological spaces and algebraic topology. | Algebraic geometry, arithmetic geometry, and Hodge theory. |
| Coefficients | Typically integers, rationals, or complexes (e.g., Z, Q, C). | Mixed coefficients including complexes and integral lattices with filtration. |
| Purpose | Measures topological invariants like holes and connectivity. | Encodes finer structures: differential forms, Hodge filtration, and periods. |
| Relation to Differential Forms | Indirect, via de Rham isomorphism. | Direct inclusion of differential forms within cohomology groups. |
| Applications | Classifying spaces, calculating topological invariants. | Study of motives, arithmetic cycles, and mixed Hodge structures. |
| Key Feature | Purely topological invariant. | Hybrid cohomology blending topology, geometry, and analysis. |
Introduction to Cohomology Theories
Betti cohomology provides topological invariants by computing singular cohomology groups with constant coefficients, capturing the shape and connectivity of complex algebraic varieties. Deligne cohomology refines this by incorporating both differential forms and integral cohomology, serving as a bridge between algebraic and analytic information through its mixed Hodge structure. These cohomology theories offer complementary tools for understanding the geometry and arithmetic of varieties, with Betti cohomology emphasizing topological aspects and Deligne cohomology encoding finer arithmetic and geometric data.
Overview of Betti Cohomology
Betti cohomology provides a topological invariant derived from the singular cohomology groups of a topological space, capturing information about the number and types of holes or cycles. It is computed using singular chains and cochains with coefficients often in a ring such as the integers, allowing classification of spaces up to homotopy equivalence. Betti cohomology contrasts with Deligne cohomology by focusing on purely topological aspects rather than incorporating additional geometric or arithmetic structures.
Fundamentals of Deligne Cohomology
Deligne cohomology combines singular Betti cohomology with sheaf cohomology and differential forms, providing a refined framework for classifying geometric objects with additional differential structure. It integrates topological information from Betti cohomology with the analytic data of differential forms, producing a cohomology theory well-suited for studying characteristic classes and arithmetic geometry. The fundamental aspect of Deligne cohomology lies in its ability to represent classes via smooth differential forms modulo integral periods, bridging topological invariants and Hodge theory.
Historical Development and Motivation
Betti cohomology originated from singular cohomology theory developed in the early 20th century to study topological spaces using continuous mappings and simplicial complexes. Deligne cohomology emerged in the 1970s as a refinement incorporating both differential forms and integral classes, motivated by the need to bridge algebraic geometry, Hodge theory, and arithmetic geometry. The historical interplay between these two theories reflects the evolution from purely topological invariants to more intricate structures capturing mixed Hodge and arithmetical information.
Key Differences: Betti vs Deligne Cohomology
Betti cohomology captures topological invariants of complex algebraic varieties using singular cohomology with integer or real coefficients, providing purely topological information. Deligne cohomology refines this by integrating both topological data and holomorphic differential forms, enabling a bridge between Hodge theory and algebraic cycles through the use of differential characters. This key difference allows Deligne cohomology to encode mixed Hodge structures and arithmetic information beyond the reach of classical Betti cohomology.
Algebraic and Topological Contexts
Betti cohomology provides topological invariants by associating singular cohomology groups with coefficients in a fixed ring, capturing the underlying space's homotopy type. Deligne cohomology refines this by incorporating both algebraic and differential structures, combining singular cohomology with sheaf-theoretic methods to classify geometric objects such as line bundles with connection in algebraic geometry. While Betti cohomology is purely topological and suited for complex analytic varieties, Deligne cohomology offers a bridge between algebraic cycles and differential forms, playing a crucial role in the study of mixed Hodge structures and arithmetic geometry.
Applications in Algebraic Geometry
Betti cohomology provides topological invariants for complex algebraic varieties, essential for understanding their continuous structure and singularities. Deligne cohomology refines this by integrating Hodge theory and differential forms, enabling classification of mixed Hodge structures and arithmetic cycles. Applications in algebraic geometry include the study of regulator maps, intermediate Jacobians, and the examination of motivic phenomena through these cohomology theories.
Relationship with Hodge Theory
Betti cohomology provides topological invariants of complex algebraic varieties by computing singular cohomology with integer or rational coefficients, capturing the space's underlying topology. Deligne cohomology refines this by incorporating differential forms and Hodge filtration, linking topological data with the complex structure through intermediate objects that interpolate between singular cohomology and the Hodge decomposition. The relationship with Hodge theory is central, as Deligne cohomology encodes mixed Hodge structures allowing the examination of variations in Hodge filtration within algebraic geometry and arithmetic contexts.
Computational Aspects and Challenges
Betti cohomology computes topological invariants of complex algebraic varieties using singular cohomology with integer coefficients, enabling relatively straightforward algorithmic implementations based on simplicial or cellular decompositions. Deligne cohomology, incorporating both topological information from Betti cohomology and differential form data, presents significant computational challenges due to the need to handle complex analytic and Hodge-theoretic structures simultaneously. Efficient algorithms for Deligne cohomology must manage the complexity of mixed Hodge structures and differential geometric inputs, making the computational process more intricate compared to the primarily combinatorial nature of Betti cohomology.
Future Directions and Open Problems
Betti cohomology, rooted in topological invariants, contrasts with Deligne cohomology's hybrid algebraic and analytic framework, posing challenges in unifying these perspectives for complex algebraic varieties. Future research aims to refine computational techniques to explicitly relate Betti and Deligne classes, enhancing understanding of arithmetic and Hodge theoretic structures. Open problems include characterizing the extension groups in Deligne cohomology that correspond to motivic phenomena and developing categorical frameworks that bridge differential forms with singular cohomology representations.
Betti cohomology Infographic
 libterm.com
libterm.com