The Delta complex is a topological space constructed by gluing together simplices along their faces, providing a fundamental framework in algebraic topology to study shapes and their properties. Understanding the structure and applications of Delta complexes can enhance your grasp of homology and other key concepts in mathematical topology. Explore the rest of the article to delve deeper into the definitions, examples, and significance of Delta complexes.
Table of Comparison
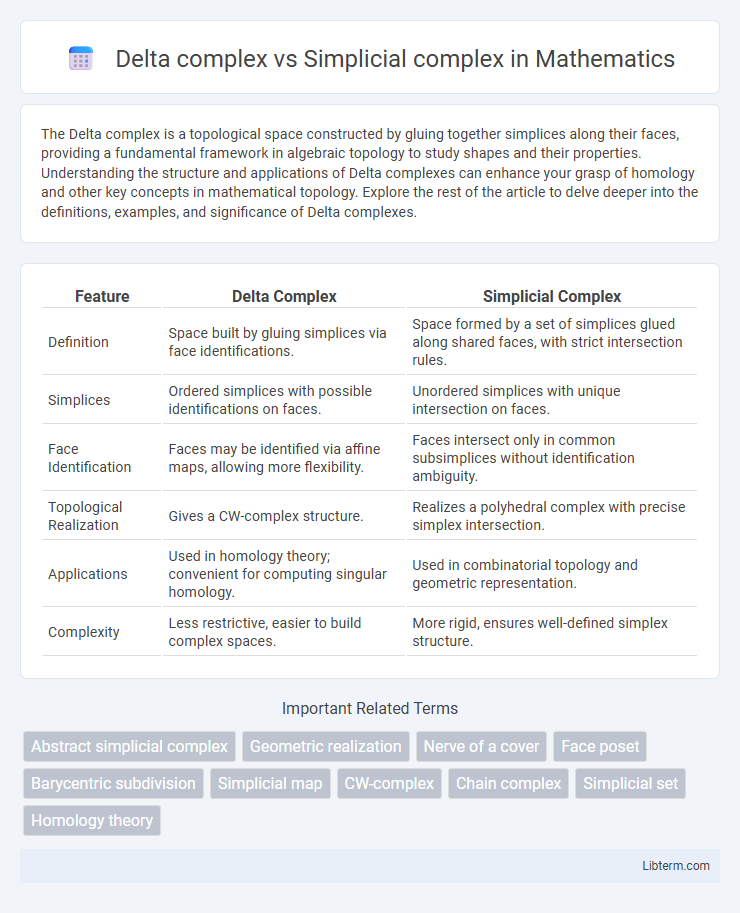
| Feature | Delta Complex | Simplicial Complex |
|---|---|---|
| Definition | Space built by gluing simplices via face identifications. | Space formed by a set of simplices glued along shared faces, with strict intersection rules. |
| Simplices | Ordered simplices with possible identifications on faces. | Unordered simplices with unique intersection on faces. |
| Face Identification | Faces may be identified via affine maps, allowing more flexibility. | Faces intersect only in common subsimplices without identification ambiguity. |
| Topological Realization | Gives a CW-complex structure. | Realizes a polyhedral complex with precise simplex intersection. |
| Applications | Used in homology theory; convenient for computing singular homology. | Used in combinatorial topology and geometric representation. |
| Complexity | Less restrictive, easier to build complex spaces. | More rigid, ensures well-defined simplex structure. |
Introduction to Complexes in Topology
Delta complexes generalize simplicial complexes by allowing simplices to be glued together along faces with identifications that are more flexible, facilitating the study of topological spaces with fewer restrictions on intersection patterns. In topology, simplicial complexes are built from simplices glued only along entire faces, making them ideal for combinatorial analysis and homology computations, while Delta complexes permit multiple face identifications, enhancing their applicability to spaces with more complex local structures. Both complexes serve as fundamental tools for decomposing spaces into manageable pieces, but Delta complexes enable a broader representation of CW complexes and more intricate cell attachments.
Defining Delta Complexes
Delta complexes are defined as a generalization of simplicial complexes where simplices are glued together along their faces without requiring the strict embeddings of simplicial complexes. Unlike simplicial complexes, delta complexes allow identification of simplices along faces that may not be injective, facilitating a more flexible combinatorial structure. This definition enables delta complexes to model topological spaces with fewer restrictions while preserving the essential properties needed for algebraic topology computations.
Understanding Simplicial Complexes
Simplicial complexes are combinatorial structures made up of vertices, edges, triangles, and their higher-dimensional counterparts, used to study topological spaces through discrete building blocks. Understanding simplicial complexes involves grasping the concept of simplices glued together along common faces, enabling the computation of topological invariants and homology groups. Unlike Delta complexes, which allow more flexible face identifications, simplicial complexes require strict adherence to simplices joining along entire faces, ensuring a well-defined combinatorial topology suitable for algebraic topology analysis.
Key Differences Between Delta and Simplicial Complexes
Delta complexes generalize simplicial complexes by allowing simplices to be glued together via affine identifications on faces, resulting in more flexible but less rigid combinatorial structures. Unlike simplicial complexes, where simplices intersect precisely along common faces, delta complexes permit face identifications that can create loops or multiple identifications, capturing spaces with more complex topologies. This flexibility in face gluings makes delta complexes particularly useful in algebraic topology for modeling spaces where strict simplicial complex conditions are too restrictive.
Construction Methods of Delta Complexes
Delta complexes are constructed by gluing simplices along their faces using face maps that preserve the order of vertices, allowing for a combinatorial structure with less rigidity than simplicial complexes. Unlike simplicial complexes, which require simplices to intersect only at shared faces with full simplex inclusion, delta complexes permit identifications that relax these constraints, enabling more flexible cell attachments. This construction method facilitates modeling spaces with quotient identifications that simplicial complexes cannot represent, making delta complexes a powerful tool in algebraic topology for representing topological spaces with singularities or non-manifold structures.
Construction Methods of Simplicial Complexes
Delta complexes construct spaces by gluing simplices along faces using face maps, allowing for identifications that maintain combinatorial structure but with less strict requirements than simplicial complexes. Simplicial complexes are built by assembling simplices so that each face of a simplex is included and the intersection of any two simplices is a face of both, ensuring a well-defined geometric realization. The construction method of simplicial complexes emphasizes strict adherence to combinatorial and topological rules that guarantee a triangulation suitable for algebraic topology applications.
Applications of Delta Complexes
Delta complexes provide a flexible framework for modeling topological spaces that accommodate non-simplicial identifications, making them especially useful in algebraic topology and geometric group theory. They enable efficient computation of homology and fundamental groups in complex spaces such as orbifolds and quotient spaces arising from group actions. Practical applications include analyzing cell structures in geometric group actions, studying moduli spaces, and simplifying constructions in category theory and homotopy theory.
Applications of Simplicial Complexes
Simplicial complexes are widely applied in topological data analysis, enabling efficient computation of homology groups to capture the shape of data in high-dimensional spaces. They provide a flexible framework for mesh generation in computer graphics and numerical simulations, facilitating the approximation of complex geometries. In contrast, Delta complexes offer a simplified combinatorial structure but are less commonly used in practical applications due to their limited flexibility in representing topological spaces.
Comparative Advantages and Limitations
Delta complexes offer a more flexible structure for modeling spaces with fewer combinatorial restrictions than simplicial complexes, enabling simpler representations of cell attachments in algebraic topology. Simplicial complexes provide stronger combinatorial properties with clearly defined vertices and simplices, facilitating more straightforward application of homology and cohomology theories. Limitations of Delta complexes include challenges in defining simplicial approximations, while simplicial complexes can suffer from combinatorial complexity and rigidity in modeling certain topologies.
Conclusion: Choosing the Right Complex for Topological Problems
Delta complexes provide a more flexible framework allowing identification of faces along arbitrary simplices, making them suitable for complex gluings and combinatorial topology problems. Simplicial complexes require strict simplices and face inclusions, offering clearer geometric intuition and simpler algebraic computations, ideal for applications needing rigid structure. Selecting between Delta and simplicial complexes depends on the balance between complexity of identifications and the need for computational tractability in topological analysis.
Delta complex Infographic
 libterm.com
libterm.com