Homotopy equivalence is a fundamental concept in algebraic topology that classifies spaces based on their continuous deformations. It captures when two spaces can be transformed into each other without tearing or gluing, preserving their essential topological features. Explore this article to understand how homotopy equivalence shapes the study of topological spaces and impacts mathematical research.
Table of Comparison
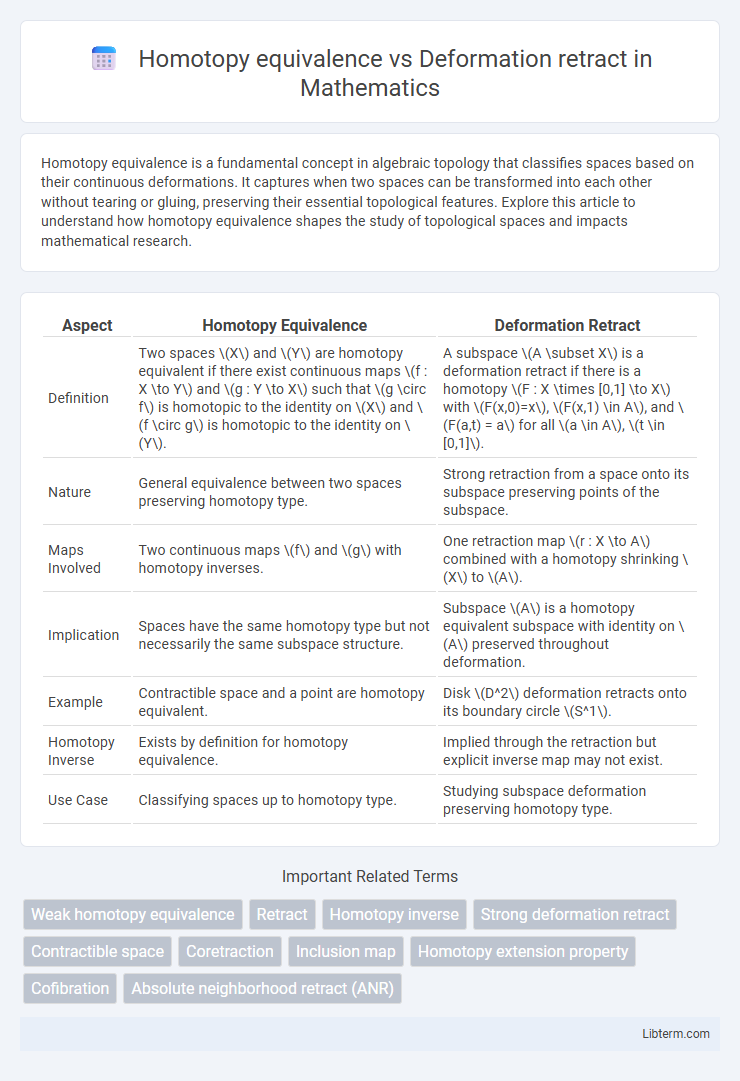
| Aspect | Homotopy Equivalence | Deformation Retract |
|---|---|---|
| Definition | Two spaces \(X\) and \(Y\) are homotopy equivalent if there exist continuous maps \(f : X \to Y\) and \(g : Y \to X\) such that \(g \circ f\) is homotopic to the identity on \(X\) and \(f \circ g\) is homotopic to the identity on \(Y\). | A subspace \(A \subset X\) is a deformation retract if there is a homotopy \(F : X \times [0,1] \to X\) with \(F(x,0)=x\), \(F(x,1) \in A\), and \(F(a,t) = a\) for all \(a \in A\), \(t \in [0,1]\). |
| Nature | General equivalence between two spaces preserving homotopy type. | Strong retraction from a space onto its subspace preserving points of the subspace. |
| Maps Involved | Two continuous maps \(f\) and \(g\) with homotopy inverses. | One retraction map \(r : X \to A\) combined with a homotopy shrinking \(X\) to \(A\). |
| Implication | Spaces have the same homotopy type but not necessarily the same subspace structure. | Subspace \(A\) is a homotopy equivalent subspace with identity on \(A\) preserved throughout deformation. |
| Example | Contractible space and a point are homotopy equivalent. | Disk \(D^2\) deformation retracts onto its boundary circle \(S^1\). |
| Homotopy Inverse | Exists by definition for homotopy equivalence. | Implied through the retraction but explicit inverse map may not exist. |
| Use Case | Classifying spaces up to homotopy type. | Studying subspace deformation preserving homotopy type. |
Introduction to Homotopy Equivalence
Homotopy equivalence is a fundamental concept in algebraic topology where two topological spaces are considered equivalent if there exist continuous maps between them whose compositions are homotopic to the identity maps. This relation preserves essential topological properties such as homotopy groups and homology groups, making it crucial in classifying spaces up to continuous deformation. A deformation retract is a stronger notion where a space can be continuously "retracted" onto a subspace while maintaining homotopy equivalence, but not all homotopy equivalences arise from deformation retracts.
Defining Deformation Retract
A deformation retract is a continuous map from a topological space onto a subspace that can be "retracted" by a homotopy, preserving the subspace identity throughout the deformation. It establishes a strong form of homotopy equivalence where the entire space is homotopically reduced to the subspace without disconnecting or altering its fundamental topological properties. This concept is central in algebraic topology for simplifying complex spaces while maintaining homotopy invariants.
Fundamental Concepts in Topology
Homotopy equivalence is a relation between topological spaces where two spaces can be continuously transformed into each other through maps that have inverses up to homotopy, preserving their essential topological properties. A deformation retract is a specific type of homotopy equivalence where a space is continuously shrunk onto a subspace, maintaining the subspace fixed during the homotopy. Both concepts play crucial roles in algebraic topology by helping classify spaces based on their homotopy type and fundamental group structures.
Homotopy Equivalence: Key Properties
Homotopy equivalence between two topological spaces X and Y implies the existence of continuous maps f: X - Y and g: Y - X where the compositions gf and fg are homotopic to the identity maps on X and Y, respectively. This relationship guarantees that X and Y share fundamental topological invariants such as homotopy groups, homology groups, and cohomology rings. Homotopy equivalence generalizes the notion of deformation retract by relaxing the requirement that one space must be a subspace of the other, focusing instead on their topological equivalence through continuous deformations.
Characterizing Deformation Retracts
A deformation retract is characterized by a homotopy between the identity map on a space X and a retraction onto a subspace A, maintaining each point of A fixed throughout the homotopy. This implies A is a strong deformation retract of X if there exists a continuous map F: X x [0,1] - X such that F(x,0) = x, F(x,1) A, and F(a,t) = a for all a in A and t in [0,1]. While homotopy equivalence ensures spaces have the same homotopy type, deformation retracts provide a stronger structure by explicitly retracting X onto A within the homotopy.
Relationship Between Homotopy Equivalence and Deformation Retracts
A deformation retract is a specific type of homotopy equivalence where a space X can be continuously contracted onto a subspace A such that A remains fixed throughout the homotopy, making A a strong deformation retract of X. Every deformation retract induces a homotopy equivalence between X and A, ensuring that their homotopy types are identical. However, homotopy equivalence is more general and does not require the fixed point condition or subspace inclusion inherent in deformation retracts.
Examples Illustrating Homotopy Equivalence
A classic example illustrating homotopy equivalence is the relationship between a solid disk and a single point, where the disk can be continuously shrunk to that point without cutting or gluing, showing they have the same homotopy type. In contrast, a deformation retract is exemplified by a circle as a deformation retract of an annulus, where the annulus can be continuously retracted onto the circle within itself, preserving the subspace structure. Homotopy equivalence encompasses deformation retracts but also includes spaces that can be stretched or compressed more flexibly, such as a coffee cup and a donut, which are homotopy equivalent but not deformation retracts of each other.
Examples of Deformation Retracts in Topology
Deformation retracts provide concrete examples in topology, such as the inclusion of a circle \( S^1 \) inside a disk \( D^2 \), where the disk can be continuously contracted onto the circle without tearing or gluing. Another classical example is the inclusion of a subspace like a wedge of spheres inside a CW complex, demonstrating that the complex deformation retracts onto the wedge, preserving homotopy type. These examples illustrate how deformation retracts serve as strong homotopy equivalences, providing explicit retractions and homotopies.
Distinctions: Homotopy Equivalence vs Deformation Retract
Homotopy equivalence between two spaces X and Y means there exist continuous maps f: X - Y and g: Y - X such that gf and fg are homotopic to the identity maps on X and Y, respectively, allowing both spaces to be deformed into each other up to homotopy. A deformation retract specifically refers to a subspace A of X with a retraction r: X - A homotopic to the identity on X that continuously shrinks X onto A while fixing A pointwise. The key distinction is that a deformation retract involves a strong deformation that fixes the subspace, making A a homotopy equivalent subspace of X, whereas homotopy equivalence does not require one space to be a subspace or the existence of a fixed-point homotopy.
Applications and Implications in Algebraic Topology
Homotopy equivalence and deformation retracts both serve as fundamental tools in algebraic topology for classifying spaces up to "shape." Deformation retracts provide a stronger condition ensuring that a subspace captures the essential topological features of the entire space, facilitating computations of homotopy groups and homology groups. Homotopy equivalence, being more general, allows for broader applications in simplifying complex spaces while preserving topological invariants crucial for tasks such as studying fiber bundles, classifying manifolds, and understanding fundamental groups.
Homotopy equivalence Infographic
 libterm.com
libterm.com