The valuative spectrum plays a crucial role in algebraic geometry by providing a topological space associated with a commutative ring that captures valuation-theoretic properties. It helps understand the structure of schemes and their local behaviors through valuations, serving as an essential tool in resolution of singularities and model theory. Explore the rest of the article to deepen your understanding of how the valuative spectrum informs modern mathematical frameworks.
Table of Comparison
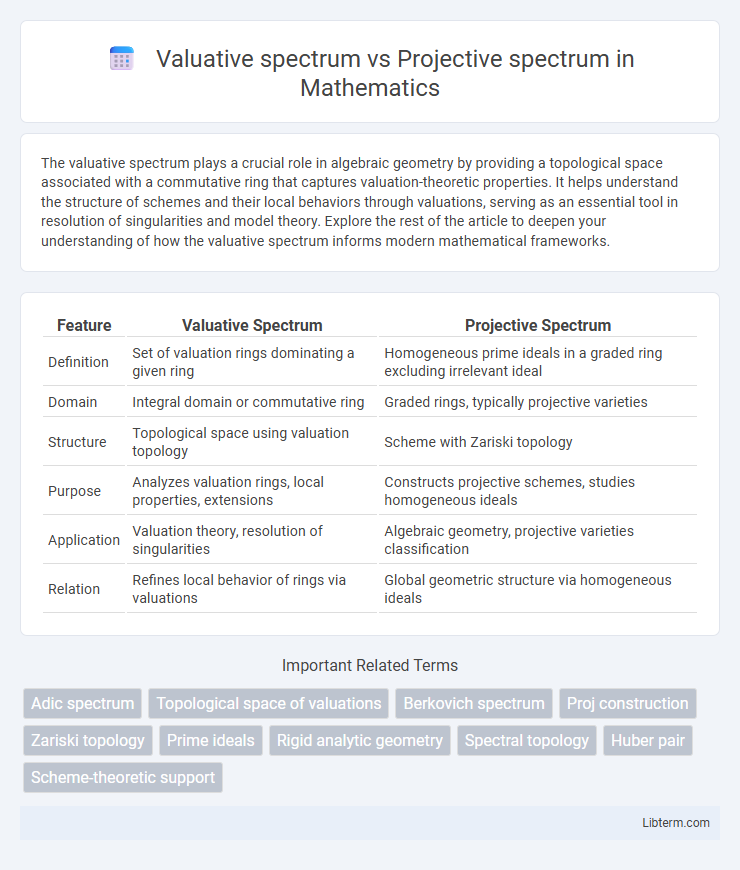
| Feature | Valuative Spectrum | Projective Spectrum |
|---|---|---|
| Definition | Set of valuation rings dominating a given ring | Homogeneous prime ideals in a graded ring excluding irrelevant ideal |
| Domain | Integral domain or commutative ring | Graded rings, typically projective varieties |
| Structure | Topological space using valuation topology | Scheme with Zariski topology |
| Purpose | Analyzes valuation rings, local properties, extensions | Constructs projective schemes, studies homogeneous ideals |
| Application | Valuation theory, resolution of singularities | Algebraic geometry, projective varieties classification |
| Relation | Refines local behavior of rings via valuations | Global geometric structure via homogeneous ideals |
Introduction to Spectrum Concepts in Algebraic Geometry
The valuative spectrum and projective spectrum are fundamental constructions in algebraic geometry that generalize the notion of spectrum associated with rings and graded rings, respectively. The valuative spectrum, denoted as Val(R), captures valuation rings dominating a given ring R, providing a finer structure related to valuations and heights. The projective spectrum, Proj(S), of a graded ring S encodes the geometric information of projective varieties by considering homogeneous prime ideals, establishing a bridge between algebraic properties and geometric objects.
Defining the Valuative Spectrum
The valuative spectrum of a ring is defined as the set of all valuation rings dominating the ring, equipped with a natural topology reflecting the inclusion relations among these valuation rings. Unlike the projective spectrum, which parameterizes homogeneous prime ideals of graded rings, the valuative spectrum captures valuations that measure the size or multiplicity of elements, offering a finer geometric insight into the ring's structure. This spectrum plays a critical role in non-archimedean geometry and valuation theory by encoding information about valuations that extend the ring's valuations in algebraic geometry.
Understanding the Projective Spectrum
The projective spectrum, denoted as Proj, is a fundamental construction in algebraic geometry that generalizes the notion of the spectrum of a ring by incorporating graded rings, enabling the study of projective varieties through homogeneous prime ideals. Unlike the valuative spectrum, which focuses on valuation rings and their associated valuation ideals to analyze local properties and value groups, the projective spectrum emphasizes graded structures and localization at homogeneous elements to understand sheaf-theoretic and geometric properties. Mastery of Proj involves comprehending its role in defining projective schemes, the use of homogeneous coordinate rings, and the formation of the associated sheaf, which together facilitate the rigorous study of projective algebraic varieties.
Key Differences Between Valuative and Projective Spectra
The valuative spectrum of a ring focuses on the set of valuation rings dominating the ring, emphasizing valuation-theoretic properties and integral extensions, while the projective spectrum (Proj) centers on homogeneous prime ideals in a graded ring, relating to algebraic geometry and projective varieties. Valuative spectra capture valuation-based local properties and are often used in valuation theory and model theory, whereas projective spectra provide a geometric object representing graded ring properties suitable for constructing projective schemes. Key differences include the valuative spectrum's valuation ring dominance criterion versus the projective spectrum's grading and prime ideal structure, influencing their roles in algebraic geometry versus valuation theory.
Structural Properties of Valuative Spectra
Valuative spectra exhibit a rich topological structure characterized by a spectral space topology, reflecting the hierarchy of valuation rings and their dominance relations. The patch topology on valuative spectra ensures compactness and spectrality, facilitating the analysis of specialization and generization among valuations. Unlike projective spectra, valuative spectra encode finer valuation-theoretic information through their structural sheaves, capturing the intrinsic valuation order and local uniformization properties.
Geometric Interpretation of Projective Spectrum
The geometric interpretation of the projective spectrum (Proj) involves associating a graded ring to a projective scheme, capturing the essence of projective varieties and their homogeneous coordinate rings. Unlike the valuative spectrum, which relates to valuation rings and local properties, Proj constructs a scheme by gluing spectra of degree-zero parts of localized rings, reflecting the geometry of projective space. This approach encodes the behavior of homogeneous ideals and their vanishing sets, providing a foundation for studying algebraic varieties in a projective context.
Applications in Algebraic Geometry
Valuative spectrum provides a tool for studying valuation rings and their extensions, playing a crucial role in the resolution of singularities and in understanding the behavior of morphisms between schemes. Projective spectrum, constructed from graded rings, is fundamental in the classification of projective varieties and the study of ampleness and line bundles in algebraic geometry. Both spectra facilitate deep insights into scheme theory, but while the valuative spectrum aids in local analysis and valuation theory, the projective spectrum focuses on global geometric properties and embedding projective schemes into projective space.
Examples Illustrating Both Spectra
The valuative spectrum of a ring R consists of all equivalence classes of valuation rings dominating R, exemplified by the valuation rings arising from discrete valuations on number fields like \(\mathbb{Q}\). The projective spectrum \(\text{Proj}(S)\) of a graded ring S, such as the polynomial ring \(\mathbb{C}[x,y]\) graded by degree, is illustrated by the projective variety \(\mathbb{P}^1\), encoding homogeneous prime ideals. Examples like the valuation ring of a discrete valuation field contrast with projective spectra of homogeneous coordinate rings, highlighting their distinct geometric and algebraic interpretations in algebraic geometry and valuation theory.
Advantages and Limitations of Each Spectrum
The valuative spectrum excels in capturing local valuation information and provides a refined topological structure sensitive to valuation rings, making it advantageous for studying local properties and integral closure. Its limitation lies in complexity and less intuitive geometric interpretation compared to classical schemes. The projective spectrum offers a more global geometric perspective through graded ring structures, facilitating the study of projective varieties and homogeneous coordinate rings, but it is less effective in analyzing detailed valuation-theoretic local data.
Conclusion: Choosing Between Valuative and Projective Spectra
Choosing between valuative and projective spectra depends on the geometric or algebraic context of the problem; valuative spectra offer a detailed local analysis by encoding valuation rings and their dominance relations, ideal for studying singularities and birational geometry. Projective spectra, constructed from graded rings, provide a global perspective facilitating the study of projective varieties and their morphisms through the Proj construction. For tasks emphasizing detailed valuation-theoretic information and local properties, valuative spectra are superior, whereas projective spectra excel in global, graded, and projective geometric contexts.
Valuative spectrum Infographic
 libterm.com
libterm.com