A strict partial order is a binary relation that is irreflexive and transitive, meaning no element relates to itself and if an element relates to a second, which relates to a third, then the first relates to the third. Common examples include the "less than" relation on numbers, where elements are ordered without ties, providing a framework for ordering without requiring comparability of every pair. Discover how strict partial orders impact structures and algorithms in the rest of the article.
Table of Comparison
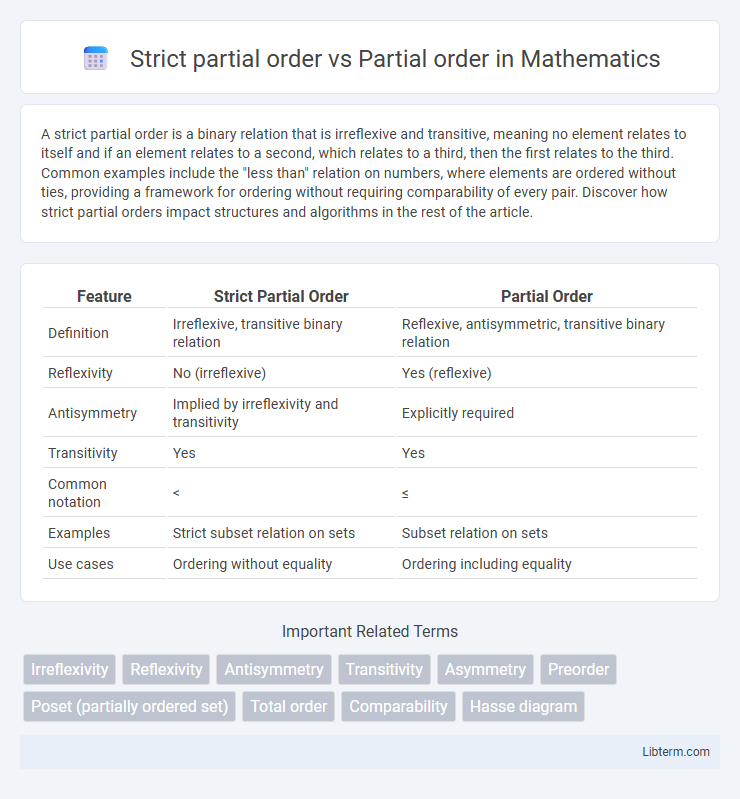
| Feature | Strict Partial Order | Partial Order |
|---|---|---|
| Definition | Irreflexive, transitive binary relation | Reflexive, antisymmetric, transitive binary relation |
| Reflexivity | No (irreflexive) | Yes (reflexive) |
| Antisymmetry | Implied by irreflexivity and transitivity | Explicitly required |
| Transitivity | Yes | Yes |
| Common notation | < | ≤ |
| Examples | Strict subset relation on sets | Subset relation on sets |
| Use cases | Ordering without equality | Ordering including equality |
Introduction to Order Relations
Partial orders define a binary relation on a set that is reflexive, antisymmetric, and transitive, establishing a hierarchy where elements may be comparable or incomparable. Strict partial orders omit reflexivity, being irreflexive, antisymmetric, and transitive, representing a "strictly less than" style relation without self-comparison. These order relations form foundational structures in mathematics and computer science for organizing data, modeling hierarchies, and enabling reasoning about precedence and dependency.
Defining Partial Order
A partial order is a binary relation over a set that is reflexive, antisymmetric, and transitive, meaning every element is related to itself, no two distinct elements precede each other mutually, and the relation follows a consistent ordering chain. Strict partial order differs by excluding reflexivity, being irreflexive, antisymmetric, and transitive, thereby imposing a "less than" style relation without equivalence to self. Defining partial order precisely requires confirming the presence of reflexivity alongside antisymmetry and transitivity to distinguish it from strict partial orders.
Understanding Strict Partial Order
A strict partial order is a binary relation that is irreflexive and transitive, meaning no element relates to itself and if an element a relates to b, and b relates to c, then a relates to c. Unlike a partial order, which allows for reflexivity where every element relates to itself, strict partial orders exclude equality in their relations. Understanding strict partial orders is essential in fields like computer science and mathematics for modeling hierarchies and precedence without equivalences.
Key Properties of Partial Orders
Partial orders are binary relations that are reflexive, antisymmetric, and transitive, ensuring every element is related to itself and no two distinct elements mutually relate, thus providing a structured hierarchy. Strict partial orders exclude reflexivity, being irreflexive and transitive, which means elements do not relate to themselves and cycles are avoided. The key properties of partial orders underpin applications in sorting algorithms, lattice theory, and data classification by establishing a clear ordering framework.
Characteristics of Strict Partial Orders
Strict partial orders are binary relations characterized by being irreflexive, transitive, and antisymmetric, meaning no element is related to itself and if an element relates to a second, which relates to a third, the first relates to the third. Unlike partial orders, strict partial orders exclude reflexivity and allow the comparison of elements without equality, emphasizing a hierarchy without self-loops. The antisymmetry in strict partial orders prevents cycle formation, ensuring a well-defined ordering structure distinct from weak or non-strict partial orders.
Differences Between Partial and Strict Partial Orders
Partial orders are binary relations on a set that are reflexive, antisymmetric, and transitive, allowing elements to relate to themselves. Strict partial orders lack reflexivity but are irreflexive, antisymmetric, and transitive, meaning no element relates to itself. The key difference lies in reflexivity: partial orders include it, enabling equality in comparisons, while strict partial orders exclude it, representing strictly less-than relationships.
Examples of Partial and Strict Partial Orders
A strict partial order is a binary relation that is irreflexive and transitive, exemplified by the "less than" relation (<) on real numbers, where no number is related to itself, and if a < b and b < c, then a < c. A partial order is reflexive, antisymmetric, and transitive, demonstrated by the "less than or equal to" relation (<=) on real numbers, where every element is related to itself, and if a <= b and b <= c, then a <= c. Strict partial orders exclude equality, while partial orders include it, making <= a common partial order and < a typical strict partial order in mathematics.
Applications in Mathematics and Computer Science
Strict partial orders, defined by irreflexivity and transitivity, are commonly applied in computer science for modeling precedence relations and scheduling problems where cycles and equality are disallowed. Partial orders, satisfying reflexivity, antisymmetry, and transitivity, are fundamental in mathematics for structuring sets with hierarchy, such as posets used in lattice theory, domain theory, and type systems. In applications like database theory, typing, and concurrency control, distinguishing between strict and non-strict relations optimizes reasoning about dependencies and state transitions.
Visualizing Partial vs Strict Partial Orders
Visualizing partial orders involves representing elements with reflexive, antisymmetric, and transitive relations, often shown using Hasse diagrams where loops indicate reflexivity. Strict partial orders omit reflexivity, illustrating only transitive and antisymmetric relations with directed edges pointing from lesser to greater elements, without loops or self-connections. This distinction allows clearer interpretation of hierarchical structures, where strict partial order diagrams emphasize strict precedence, while partial order diagrams reveal inclusive relationships.
Summary: Choosing the Appropriate Order Relation
Strict partial orders are irreflexive and transitive, ideal for modeling scenarios where no element relates to itself, such as "less than" relations. Partial orders are reflexive, antisymmetric, and transitive, suitable for hierarchical structures where elements can be comparable or equal, like subset relations. Selecting the appropriate order relation depends on whether self-comparison is meaningful and the nature of element comparability in the data or system being modeled.
Strict partial order Infographic
 libterm.com
libterm.com