Cofinal specializes in providing comprehensive financial services tailored to meet the unique needs of businesses seeking reliable funding solutions. Their expertise spans from loan acquisition to financial consulting, ensuring your company achieves sustainable growth and stability. Discover how Cofinal can transform your financial strategy by reading the full article.
Table of Comparison
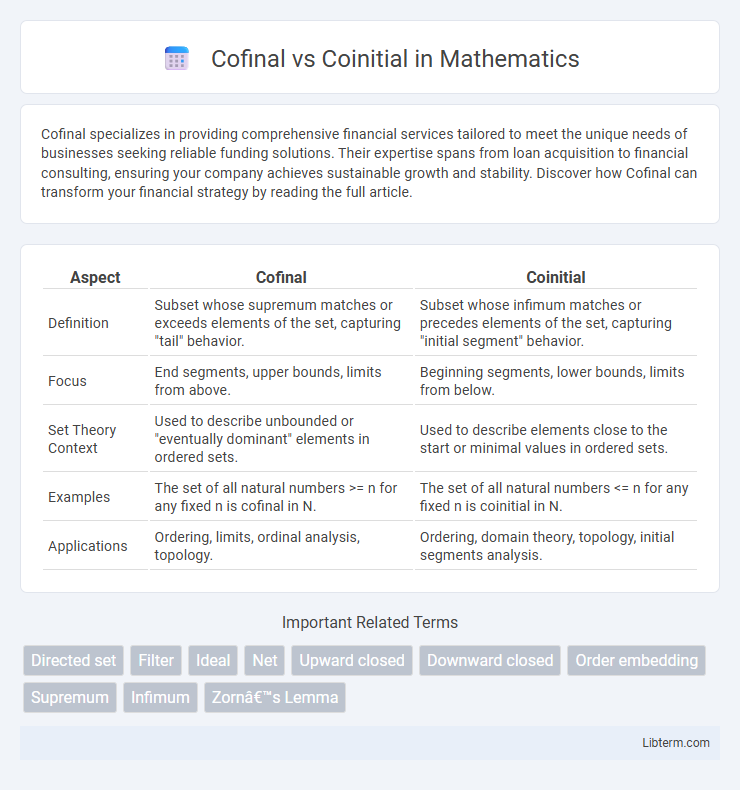
| Aspect | Cofinal | Coinitial |
|---|---|---|
| Definition | Subset whose supremum matches or exceeds elements of the set, capturing "tail" behavior. | Subset whose infimum matches or precedes elements of the set, capturing "initial segment" behavior. |
| Focus | End segments, upper bounds, limits from above. | Beginning segments, lower bounds, limits from below. |
| Set Theory Context | Used to describe unbounded or "eventually dominant" elements in ordered sets. | Used to describe elements close to the start or minimal values in ordered sets. |
| Examples | The set of all natural numbers >= n for any fixed n is cofinal in N. | The set of all natural numbers <= n for any fixed n is coinitial in N. |
| Applications | Ordering, limits, ordinal analysis, topology. | Ordering, domain theory, topology, initial segments analysis. |
Understanding Cofinal and Coinitial: Key Definitions
Cofinal and coinitial refer to properties of subsets within ordered sets, where a cofinal subset contains elements that eventually exceed any given element of the original set, ensuring it is unbounded above. A coinitial subset contains elements that are eventually smaller than any given element of the set, making it unbounded below. Understanding these definitions is fundamental for applications in order theory and topology, where they help characterize the structural behavior of ordered sets and their bounds.
The Mathematical Context of Cofinality and Coinitiality
Cofinality in order theory measures the smallest size of an unbounded subset within a partially ordered set, indicating the minimal cardinality needed to "reach" the entire set via upward-directedness. Coinitiality, or coinitial order type, is the dual concept describing the minimal cardinality of a downward unbounded subset, reflecting how the order type is approached from below. These concepts are fundamental in analyzing ordinal numbers, directed sets, and chain conditions in mathematical structures such as lattices and posets.
Differences Between Cofinal and Coinitial
Cofinal refers to a subset or sequence that eventually reaches or matches the supremum of a partially ordered set, while coinitial describes a subset or sequence that approaches the infimum. The primary difference lies in their directional focus: cofinal sequences move upward toward the greatest element, whereas coinitial sequences move downward toward the least element. In topology or order theory, identifying cofinal subsets helps analyze limits from above, whereas coinitial subsets are crucial for studying limits from below.
Cofinal Sets: Examples and Applications
Cofinal sets are subsets of a partially ordered set where every element in the entire set is less than or equal to some element in the cofinal subset, ensuring the subset is unbounded above. For example, in the set of natural numbers \(\mathbb{N}\), the set of all natural numbers greater than 100 is cofinal since every natural number is less than or equal to some number in this subset. Cofinal sets are crucial in order theory and topology, particularly in analyzing directed sets, filtering limits, and studying ordinal numbers.
Coinitial Sets: Examples and Applications
Coinitial sets are collections in order theory where every element has a common lower bound, meaning all elements lie above a specific element in the partially ordered set. Examples include the set of all real numbers greater than zero within the real number line, where zero serves as a coinitial element. Applications of coinitial sets appear in lattice theory and domain theory, aiding in fixed point computations and the study of convergence properties.
Cofinality in Order Theory
Cofinality is a fundamental concept in order theory describing the smallest cardinality of a subset needed to be unbounded in a partially ordered set, ensuring every element of the set is less than or equal to some element of this subset. Unlike coinitiality, which concerns the smallest subset unbounded below, cofinality captures the complexity of representing an order type through its "end segments." Understanding cofinality aids in analyzing ordinal numbers, cardinality, and the structure of infinite sets within set theory.
Coinitiality in Order Theory
Coinitiality in order theory refers to a subset of a partially ordered set that intersects every initial segment, ensuring that the subset is "co-final" in the dual order. Unlike cofinal subsets which meet every final segment, coinitial subsets are crucial for understanding the structure of ordered sets from below, helping characterize completeness and continuity properties. Studying coinitiality aids in analyzing order topology, filters, and ideals by providing insight into the foundational elements that define order convergence and density.
Cofinal vs Coinitial: Common Confusions
Cofinal and coinitial are terms used in order theory to describe elements related to sequences or sets. Cofinal refers to a subset of a partially ordered set whose elements are greater than or equal to every element in the original set, capturing the "tail" behavior, while coinitial describes subsets where elements are less than or equal to those in the original set, indicating the "initial" segment. Common confusions arise because both concepts deal with bounds and limits, but cofinality focuses on upper bounds whereas coinitiality emphasizes lower bounds.
Implications in Set Theory and Beyond
Cofinal and coinitial subsets play critical roles in understanding order types, cardinalities, and embeddings within set theory and beyond. Cofinal sets characterize unboundedness in partially ordered sets and are essential for defining limits, suprema, and completeness properties, while coinitial sets identify minimal initial segments crucial in dual notions and order duality. These concepts impact areas such as topology, model theory, and algebra by facilitating the study of convergence, ultrafilters, and morphisms in directed systems.
Summary: Comparing Cofinal and Coinitial Concepts
Cofinal and coinitial concepts describe the relationship between subsets within partially ordered sets, where a subset is cofinal if every element in the larger set is less than or equal to some element of the subset, and coinitial if every element in the larger set is greater than or equal to some element of the subset. In lattice theory and order theory, cofinal subsets help identify limits and bounds from above, while coinitial subsets relate to limits and bounds from below. Understanding these distinctions is essential for analyzing directed sets, nets, and filters in topology and algebra.
Cofinal Infographic
 libterm.com
libterm.com