Infinite concepts challenge our understanding of limits and boundlessness, spanning mathematics, philosophy, and cosmology. Exploring infinity reveals profound implications for the universe's structure and the nature of existence itself. Dive into the article to uncover the fascinating depths of infinite possibilities and their impact on Your perspective.
Table of Comparison
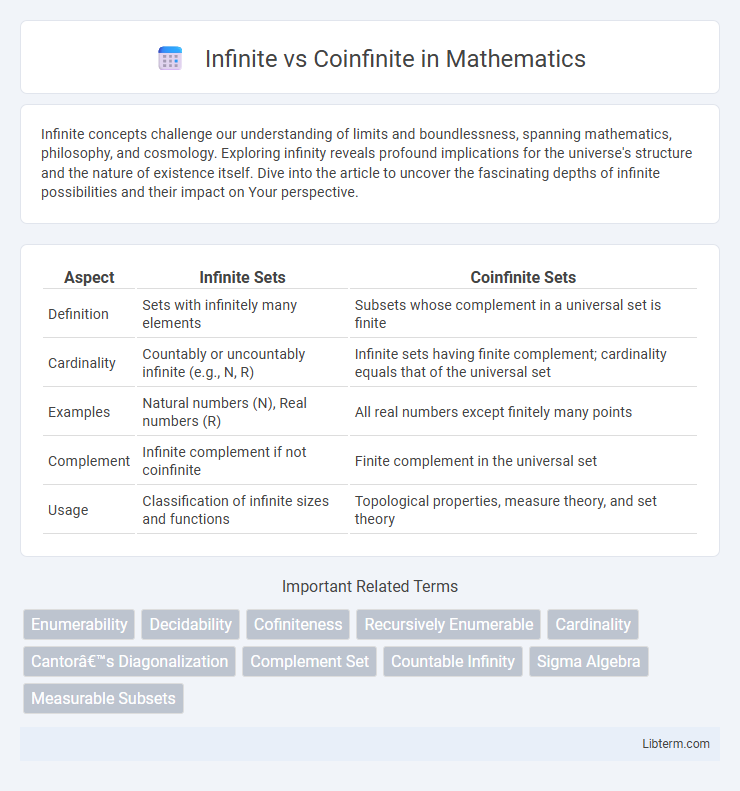
| Aspect | Infinite Sets | Coinfinite Sets |
|---|---|---|
| Definition | Sets with infinitely many elements | Subsets whose complement in a universal set is finite |
| Cardinality | Countably or uncountably infinite (e.g., N, R) | Infinite sets having finite complement; cardinality equals that of the universal set |
| Examples | Natural numbers (N), Real numbers (R) | All real numbers except finitely many points |
| Complement | Infinite complement if not coinfinite | Finite complement in the universal set |
| Usage | Classification of infinite sizes and functions | Topological properties, measure theory, and set theory |
Understanding Infinite and Coinfinite Sets
Infinite sets contain an unending number of elements, such as the set of natural numbers, illustrating that their size cannot be measured by finite means. Coinfinite sets are subsets whose complements within a larger infinite set are finite, meaning the original set almost entirely covers the infinite set except for a limited number of elements. Recognizing the difference between infinite and coinfinite sets is crucial for understanding their applications in set theory, topology, and computer science.
Key Differences Between Infinite and Coinfinite
Infinite refers to a set or quantity without any limit or end, often used in mathematics to describe unbounded values or sequences. Coinfinite, however, specifically denotes the complement of a finite set within an infinite universal set, meaning it includes all elements except a finite number. The key difference lies in infinite representing limitless size, while coinfinite relates to everything outside a finite subset within an infinite context.
Mathematical Definitions and Formalism
Infinite refers to a set or quantity without any finite bounds, characterized by its unending size or magnitude, often formalized in set theory using concepts like cardinality and ordinality. Coinfinite describes subsets of a larger infinite set whose complements are finite, meaning that the remaining elements outside the subset form a limited or finite set. In mathematical formalism, if \(A\) is a subset of an infinite set \(S\), then \(A\) is coinfinite if \(S \setminus A\) is finite, highlighting the duality between infinite and coinfinite properties in measure and topology contexts.
Infinite Sets: Examples and Properties
Infinite sets include examples such as natural numbers, integers, and real numbers, characterized by having no finite cardinality. Key properties involve their ability to be put into one-to-one correspondence with proper subsets, exemplified by the set of natural numbers and even numbers. Unlike finite sets, infinite sets demonstrate different types of infinity, notably countable and uncountable cardinalities, crucial for understanding set theory and mathematical analysis.
Coinfinite Sets: Examples and Characteristics
Coinfinite sets are subsets of a universal set whose complements are finite, meaning they contain all but finitely many elements of the universal set. For example, if the universal set is the natural numbers, the set of all natural numbers except for a finite number of values, such as all numbers except {1, 2, 3}, is coinfinite. Key characteristics of coinfinite sets include having infinite cardinality, being coextensive with almost the entire universal set, and typically appearing in set theory and topology when analyzing properties related to infinite complements and large subsets.
Infinite vs Coinfinite in Set Theory
Infinite sets are collections with an unbounded number of elements, exhibiting properties such as equivalence in cardinality with proper subsets, as demonstrated by Cantor's diagonal argument. Coinfinite sets are complements of finite sets within a universal set, meaning the remaining elements form a set whose size is infinite because only finitely many elements are excluded. The distinction between infinite and coinfinite sets is crucial in set theory for understanding cardinality, measure theory, and the behavior of infinite combinatorial structures.
Intersection and Union: Infinite and Coinfinite Sets
Infinite sets contain infinitely many elements, while coinfinite sets have complements that are infinite, making their union and intersection properties essential in set theory. The intersection of an infinite set and a coinfinite set can be finite, infinite, or even empty, depending on the specific elements they share. Their union typically results in a cofinite set if one is infinite and the other is coinfinite, showcasing fundamental relationships in infinite set operations.
Countable vs Uncountable: Infinite and Coinfinite Aspects
Infinite sets are countable when their elements can be bijectively mapped to the natural numbers, such as the set of integers, while uncountable infinite sets, like the real numbers, lack such mappings. Coinfinite sets in a given universe have complements that are finite, making them nearly complete within that domain, and this property is crucial in distinguishing countable and uncountable infinites. The interplay between infinite, countable, and coinfinite sets forms the foundation for understanding cardinalities and the structure of subsets in set theory.
Applications of Infinite and Coinfinite Sets
Infinite sets find broad applications in number theory, calculus, and computer science, particularly in defining concepts like infinite sequences, series, and algorithmic complexity. Coinfinite sets, those with finite complements in infinite sets, are crucial in topology and measure theory for characterizing dense subsets and measurable spaces. Their applications extend to ergodic theory and combinatorics, where understanding the structure of coinfinite sets aids in solving problems involving infinite configurations with finite exceptions.
Common Misconceptions About Infinite and Coinfinite
Infinite and coinfinite sets are often misunderstood as having similar properties due to their related definitions in set theory. A common misconception is that coinfinite sets must be finite complements of infinite sets, while in reality, coinfinite sets specifically have infinite complements that are not necessarily finite. Clarifying that infinite sets can have infinite or finite complements helps distinguish the nuanced roles of infinite and coinfinite in mathematical contexts.
Infinite Infographic
 libterm.com
libterm.com