Injective resolution plays a critical role in homological algebra by providing a method to study modules through injective modules. This construction allows for the computation of derived functors, such as Ext, by replacing a given module with an exact sequence of injective modules. Explore the rest of the article to deepen your understanding of injective resolutions and their applications in algebraic contexts.
Table of Comparison
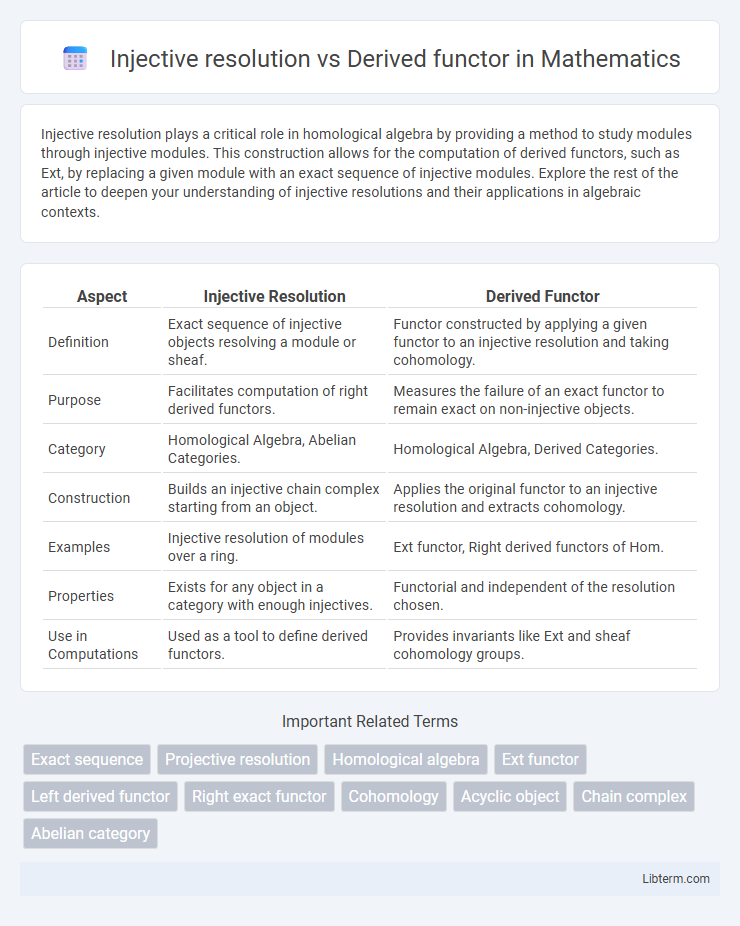
| Aspect | Injective Resolution | Derived Functor |
|---|---|---|
| Definition | Exact sequence of injective objects resolving a module or sheaf. | Functor constructed by applying a given functor to an injective resolution and taking cohomology. |
| Purpose | Facilitates computation of right derived functors. | Measures the failure of an exact functor to remain exact on non-injective objects. |
| Category | Homological Algebra, Abelian Categories. | Homological Algebra, Derived Categories. |
| Construction | Builds an injective chain complex starting from an object. | Applies the original functor to an injective resolution and extracts cohomology. |
| Examples | Injective resolution of modules over a ring. | Ext functor, Right derived functors of Hom. |
| Properties | Exists for any object in a category with enough injectives. | Functorial and independent of the resolution chosen. |
| Use in Computations | Used as a tool to define derived functors. | Provides invariants like Ext and sheaf cohomology groups. |
Introduction to Injective Resolutions and Derived Functors
Injective resolutions are exact sequences of injective modules used to compute derived functors, providing a framework to extend functorial properties beyond exactness. Derived functors, such as Ext and Tor, are constructed by applying a functor to an injective or projective resolution and taking homology, capturing deeper structural information of modules or sheaves. This approach links homological algebra concepts, facilitating computations in cohomology theories and other advanced algebraic contexts.
Foundations: Modules, Functors, and Homological Algebra
Injective resolutions serve as essential tools in homological algebra, providing exact sequences of injective modules that allow the computation of right derived functors, such as Ext and right derived Hom. Within the foundations of modules and functors, derived functors extend the classical functor concept by measuring the failure of exactness, systematically capturing higher-dimensional cohomological information. These constructions underpin advanced study in module categories by enabling the analysis of complex algebraic structures through their homological properties and exactness behavior.
What is an Injective Resolution?
An injective resolution is a chain complex of injective modules used to compute derived functors in homological algebra, serving as a tool to extend the domain of left exact functors. It replaces a given module with an exact sequence whose terms are injective modules, allowing the calculation of right derived functors such as Ext and right derived functors of Hom. The injective resolution ensures that homological invariants can be extracted from objects that may not be injective by construction, facilitating deeper analysis in module theory and algebraic geometry.
Understanding Derived Functors
Derived functors provide a systematic way to extend a given functor to compute homological invariants, typically by replacing objects with injective resolutions when working with right derived functors. Understanding derived functors involves recognizing that they measure the failure of exactness of the original functor and can be realized by applying the functor to an injective resolution and taking cohomology. Injective resolutions play a crucial role in constructing these derived functors, enabling computations of Ext and higher Tor groups in homological algebra.
Constructing Injective Resolutions: Step-by-Step
Constructing injective resolutions begins by embedding a given module into an injective module, ensuring the inclusion is a monomorphism. Subsequent steps involve iteratively defining cokernels and embedding these cokernels into injective modules, forming an exact sequence whose terms are injective. This resolution enables computing derived functors like Ext, as the process replaces complicated objects with well-understood injective ones facilitating homological algebra computations.
The Role of Injective Resolutions in Defining Derived Functors
Injective resolutions play a fundamental role in defining derived functors by providing a systematic method to extend functors from objects to complexes in homological algebra. They allow the computation of right derived functors, such as Ext and higher cohomology groups, by replacing modules with exact complexes of injective modules where the original functor remains exact. This approach ensures that the derived functor captures homological information beyond exact sequences, facilitating deeper analysis of module structures and morphisms.
Comparing Injective Resolutions and Derived Functors
Injective resolutions provide the foundational framework for defining derived functors by allowing exact sequences to be extended into injective objects, facilitating homological calculations. Derived functors systematically extract homological invariants from non-exact functors using these injective resolutions, ensuring the preservation of essential algebraic structures. Comparing injective resolutions and derived functors highlights how the former serves as a computational tool, while the latter generalizes and interprets the resulting homological information.
Examples: Ext and Tor via Injective and Projective Resolutions
Ext groups can be computed using injective resolutions by applying the Hom functor to an injective resolution of a module, revealing extensions between modules. Tor groups arise from applying the tensor product functor to a projective resolution of a module, measuring the non-flatness of modules. These constructions exemplify how derived functors of Hom and tensor product capture deeper homological properties through injective and projective resolutions, respectively.
Applications in Cohomology and Algebraic Geometry
Injective resolutions provide a foundational tool for computing derived functors, which are essential in extracting cohomological information from complex algebraic structures. In cohomology and algebraic geometry, derived functors such as Ext and Tor are typically computed via injective or projective resolutions, enabling the analysis of sheaf cohomology and local cohomology groups on schemes. The interplay between injective resolutions and derived functors facilitates the understanding of deeper geometric properties through spectral sequences and supports the formulation of duality theorems in algebraic geometry.
Summary: Key Differences and Practical Implications
Injective resolution involves constructing an exact sequence of injective modules to compute right derived functors, serving as a foundational tool in homological algebra. Derived functors generalize homology by measuring the failure of exactness of a functor, using injective resolutions to extend their domain beyond projective or free modules. Practically, injective resolutions enable explicit calculations of derived functors like Ext and right-derived Hom, crucial for applications in cohomology theories and sheaf theory.
Injective resolution Infographic
 libterm.com
libterm.com