Subadditive functions exhibit the property where the function's value at the sum of inputs is less than or equal to the sum of the function's values at each input individually, a key concept in mathematics and economics. This characteristic plays a crucial role in optimization problems, cost analysis, and risk assessment. Explore the rest of the article to understand how subadditivity impacts various fields and practical applications.
Table of Comparison
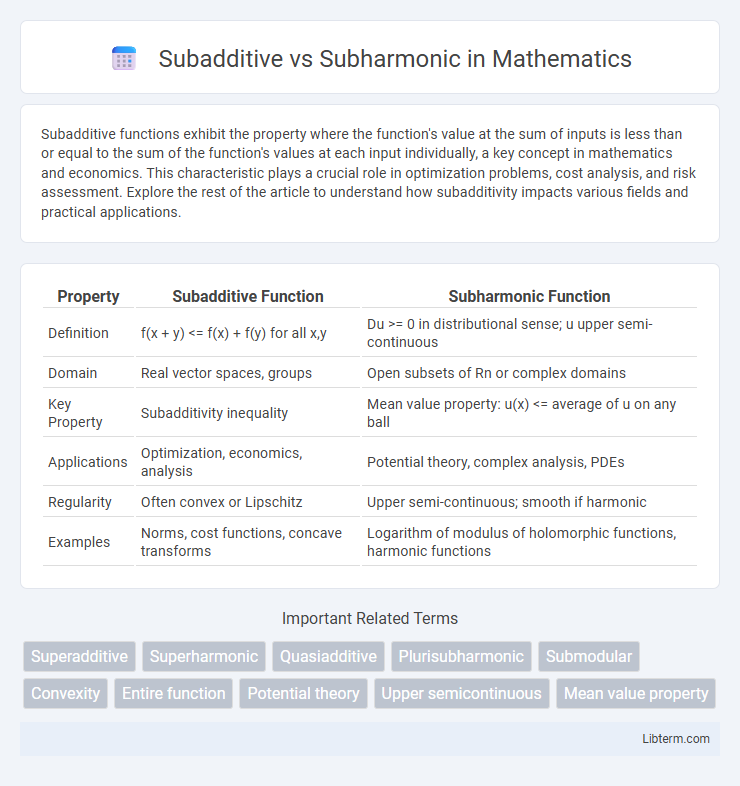
| Property | Subadditive Function | Subharmonic Function |
|---|---|---|
| Definition | f(x + y) <= f(x) + f(y) for all x,y | Du >= 0 in distributional sense; u upper semi-continuous |
| Domain | Real vector spaces, groups | Open subsets of Rn or complex domains |
| Key Property | Subadditivity inequality | Mean value property: u(x) <= average of u on any ball |
| Applications | Optimization, economics, analysis | Potential theory, complex analysis, PDEs |
| Regularity | Often convex or Lipschitz | Upper semi-continuous; smooth if harmonic |
| Examples | Norms, cost functions, concave transforms | Logarithm of modulus of holomorphic functions, harmonic functions |
Introduction to Subadditive and Subharmonic Functions
Subadditive functions satisfy the inequality f(x + y) <= f(x) + f(y) for all x, y in their domain, reflecting diminishing returns or aggregation properties. Subharmonic functions, defined on open subsets of Euclidean space, are upper semi-continuous and satisfy the mean value inequality involving Laplace operators, meaning their value at a point is less than or equal to the average over any surrounding sphere. Both function classes play crucial roles in analysis and potential theory, with subadditive functions often linked to optimization and economics, while subharmonic functions connect to complex analysis and partial differential equations.
Defining Subadditivity: Meaning and Examples
Subadditivity refers to a property of a function \( f \) where for all inputs \( x \) and \( y \), the inequality \( f(x + y) \leq f(x) + f(y) \) holds. This concept is commonly applied in areas such as probability theory, economics, and optimization, exemplified by cost functions where combining resources leads to less total cost than individual sums. Subharmonic functions, in contrast, relate to harmonic analysis and partial differential equations, representing functions whose value at any point is less than or equal to the average on any surrounding neighborhood, differing fundamentally from subadditive functions in both definition and application.
Understanding Subharmonicity: Core Concepts
Subharmonicity refers to functions that satisfy the subharmonic inequality, meaning their value at a point is less than or equal to the average value over any surrounding sphere, reflecting a generalized form of harmonic functions. Unlike subadditive functions, which exhibit the inequality f(x + y) <= f(x) + f(y) related to algebraic structures, subharmonic functions arise in potential theory and partial differential equations, emphasizing their analytical and geometric properties. Understanding subharmonicity involves exploring concepts like mean value properties, maximum principles, and the Laplace operator's role, which are fundamental to complex analysis and mathematical physics.
Key Differences Between Subadditive and Subharmonic
Subadditive functions satisfy the inequality f(x + y) <= f(x) + f(y) for all x, y in their domain, emphasizing additive properties in real analysis and optimization contexts. Subharmonic functions, crucial in complex analysis and potential theory, are upper semi-continuous functions that satisfy the mean value property where the value at a point is less than or equal to the average over any surrounding circle or sphere. The key difference lies in their definitions and applications: subadditivity relates to function growth constraints under addition, while subharmonicity involves harmonic function comparison and potential theoretic bounds in partial differential equations.
Mathematical Properties of Subadditive Functions
Subadditive functions f satisfy the inequality f(x + y) <= f(x) + f(y) for all x, y in their domain, reflecting a key property used in optimization and measure theory. These functions exhibit convex-like behavior without necessarily being convex, often enabling effective bounds in economics, probability, and functional analysis. Unlike subharmonic functions, which are linked to Laplace operators and harmonic functions, subadditive functions focus on additive inequalities that govern growth and aggregation in mathematical modeling.
Essential Properties of Subharmonic Functions
Subharmonic functions are upper semicontinuous and satisfy the mean value property, where their value at any point is less than or equal to the average over any surrounding sphere, ensuring they cannot attain a local maximum inside the domain unless they are constant. Unlike subadditive functions, which are defined by the inequality f(x + y) <= f(x) + f(y), subharmonic functions are closely related to harmonic functions and obey the Laplace inequality Du >= 0 in the distributional sense. Essential properties include their stability under taking maxima, limits of sequences, and convolution with smooth mollifiers, making them fundamental in potential theory and complex analysis.
Applications of Subadditive Functions in Optimization
Subadditive functions, characterized by the property f(x+y) <= f(x) + f(y), are crucial in optimization, especially in areas like cost minimization, resource allocation, and network design, where combining inputs leads to economies of scale or efficiency gains. Unlike subharmonic functions, which arise primarily in potential theory and partial differential equations, subadditive functions provide a structural framework for analyzing and solving large-scale optimization problems through techniques such as dynamic programming and convex analysis. The subadditivity property ensures stability and convergence in iterative optimization algorithms, making it essential in operations research and algorithmic design.
Subharmonic Functions in Complex Analysis and Potential Theory
Subharmonic functions in complex analysis are upper semicontinuous functions that satisfy the mean value property, where their value at a point is less than or equal to the average over any surrounding circle, playing a crucial role in potential theory and the study of harmonic and holomorphic functions. These functions are pivotal in understanding Laplace's equation, as every harmonic function is subharmonic, but not all subharmonic functions are harmonic, highlighting the broader class they form. Subharmonicity provides essential tools for analyzing growth properties, singularities, and boundary behaviors in complex and potential theory contexts.
Comparative Analysis: When to Use Subadditive vs Subharmonic
Subadditive functions, characterized by the inequality f(x + y) <= f(x) + f(y), are essential in optimization problems and economic models involving cost minimization or resource allocation. Subharmonic functions, defined through mean value properties and differential inequalities like Du >= 0, play a critical role in potential theory and complex analysis, helping to model phenomena such as heat distribution or electrostatics. Use subadditive functions when analyzing systems requiring aggregation or cumulative effects, whereas subharmonic functions are preferred for problems involving harmonicity, boundary behavior, and partial differential equations.
Conclusion: Practical Implications and Further Reading
Subadditive functions, characterized by f(x + y) <= f(x) + f(y), often appear in economics and optimization, emphasizing cost efficiency and resource allocation. Subharmonic functions, defined by the mean value inequality in potential theory, offer critical insights in complex analysis and partial differential equations. Exploring foundational texts such as "Classical Potential Theory" by Armitage and Gardiner alongside "Convex Analysis" by Rockafellar provides deeper understanding and practical applications in mathematical modeling and analysis.
Subadditive Infographic
 libterm.com
libterm.com