A metric space is a set equipped with a metric, a function that defines the distance between any two elements, satisfying specific properties like non-negativity, identity of indiscernibles, symmetry, and the triangle inequality. This concept forms the foundation for analyzing convergence, continuity, and compactness in mathematics. Dive deeper into this article to explore how metric spaces influence various branches of mathematical theory and applications.
Table of Comparison
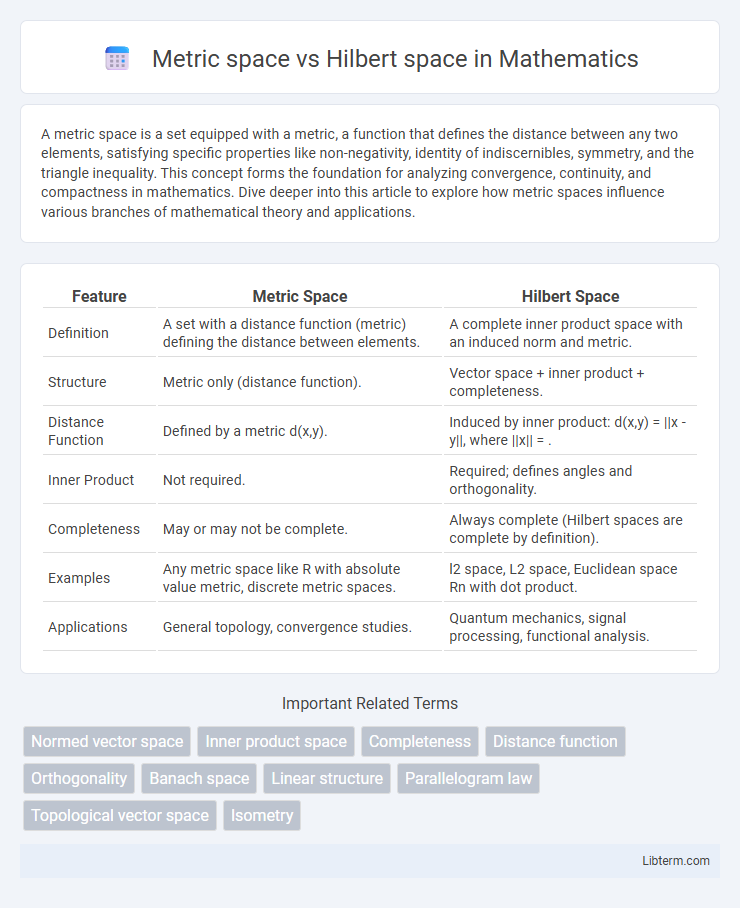
| Feature | Metric Space | Hilbert Space |
|---|---|---|
| Definition | A set with a distance function (metric) defining the distance between elements. | A complete inner product space with an induced norm and metric. |
| Structure | Metric only (distance function). | Vector space + inner product + completeness. |
| Distance Function | Defined by a metric d(x,y). | Induced by inner product: d(x,y) = ||x - y||, where ||x|| = |
| Inner Product | Not required. | Required; defines angles and orthogonality. |
| Completeness | May or may not be complete. | Always complete (Hilbert spaces are complete by definition). |
| Examples | Any metric space like R with absolute value metric, discrete metric spaces. | l2 space, L2 space, Euclidean space Rn with dot product. |
| Applications | General topology, convergence studies. | Quantum mechanics, signal processing, functional analysis. |
Introduction to Metric Spaces and Hilbert Spaces
Metric spaces provide a fundamental framework in topology by defining a set equipped with a distance function satisfying non-negativity, symmetry, and the triangle inequality, enabling analysis of convergence and continuity. Hilbert spaces extend this concept by incorporating an inner product structure that induces a metric, allowing the generalization of Euclidean geometry to infinite-dimensional spaces and facilitating techniques in functional analysis and quantum mechanics. Understanding the distinctions and applications of metric and Hilbert spaces is essential for advanced studies in mathematical analysis and related fields.
Defining Metric Spaces: Key Properties
Metric spaces are defined by a distance function (metric) satisfying non-negativity, identity of indiscernibles, symmetry, and the triangle inequality, providing a generalized notion of distance between elements. This structure enables analysis of convergence, continuity, and compactness without requiring linearity or inner products. Hilbert spaces extend metric spaces by incorporating an inner product that induces the metric, offering richer geometric and algebraic properties essential for advanced functional analysis.
Defining Hilbert Spaces: Core Concepts
Hilbert spaces are a special class of metric spaces characterized by an inner product that defines the norm and distance, enabling geometrical and analytical properties such as orthogonality and projection. Unlike general metric spaces that only require a distance function satisfying positivity, symmetry, and triangle inequality, Hilbert spaces must be complete with respect to the norm induced by the inner product. Key core concepts of Hilbert spaces include the inner product, completeness, orthonormal bases, and the ability to perform projections, making them fundamental in functional analysis and quantum mechanics.
Similarities Between Metric and Hilbert Spaces
Metric spaces and Hilbert spaces both provide a framework for measuring distances between elements, with metric spaces defining a general distance function and Hilbert spaces incorporating an inner product that induces this metric. Both spaces are complete with respect to their metrics when they are considered complete metric spaces and complete inner product spaces, respectively, allowing convergence of sequences within the space. They share foundational roles in analysis and topology, enabling rigorous treatment of notions like continuity, convergence, and compactness through their distance structures.
Key Differences: Metric Spaces vs Hilbert Spaces
Metric spaces are sets equipped with a distance function (metric) that defines the distance between any two points, ensuring properties like non-negativity, symmetry, and the triangle inequality. Hilbert spaces extend metric spaces by including an inner product that induces the metric, allowing notions of angle, orthogonality, and projection, crucial in functional analysis and quantum mechanics. Unlike general metric spaces, Hilbert spaces are complete inner product spaces, meaning every Cauchy sequence converges within the space, enabling advanced geometric and analytical techniques.
Geometric Interpretations in Each Space
Metric spaces provide a general framework for measuring distances between points using a defined metric, allowing geometric interpretations such as convergence, continuity, and the shape of sets through open and closed balls. Hilbert spaces extend these concepts by introducing an inner product that enables angles and orthogonality, facilitating more refined geometric structures like projections, orthonormal bases, and decomposition of vectors. The geometric intuition in Hilbert spaces closely resembles Euclidean geometry, enabling advanced tools in functional analysis and quantum mechanics.
Examples of Metric Spaces
Metric spaces include examples such as the Euclidean space \(\mathbb{R}^n\) with the standard distance metric, discrete metric spaces where the distance between distinct points is one, and function spaces equipped with metrics like the supremum metric. Unlike Hilbert spaces, metric spaces need not have an inner product or completeness with respect to it. This distinction is crucial since Hilbert spaces, a subclass of metric spaces, require an inner product that induces the metric and completeness under this inner product norm.
Examples of Hilbert Spaces
Hilbert spaces are complete inner product spaces that generalize Euclidean space to infinite dimensions, commonly exemplified by spaces like \( \ell^2 \), the set of square-summable sequences, and \( L^2(\mathbb{R}) \), the space of square-integrable functions over the real line. Unlike general metric spaces, which only require a distance function satisfying metric axioms, Hilbert spaces possess an inner product inducing the norm and metric, enabling geometric concepts such as orthogonality and projections. Classic examples include Sobolev spaces used in partial differential equations and Fourier analysis spaces crucial for signal processing and quantum mechanics.
Applications: Where to Use Metric or Hilbert Spaces
Metric spaces provide a versatile framework for analyzing distance and convergence in various fields such as computer science, optimization, and topology, making them ideal for problems involving general notions of distance without requiring an inner product. Hilbert spaces, equipped with an inner product, are essential in quantum mechanics, signal processing, and functional analysis due to their structure supporting orthogonality, projections, and Fourier transforms. Applications in machine learning and statistics often prefer Hilbert spaces like reproducing kernel Hilbert spaces (RKHS) for their rich geometric properties facilitating kernel methods and high-dimensional data analysis.
Summary: Choosing Between Metric and Hilbert Spaces
Metric spaces provide a broad framework characterized by a distance function satisfying positivity, symmetry, and the triangle inequality, suitable for general analysis and topology. Hilbert spaces, as complete inner product spaces, offer structure through inner products that enable geometric concepts like orthogonality and projections, essential for quantum mechanics and signal processing. The choice between metric and Hilbert spaces depends on the need for linear algebraic operations and geometric intuition versus more general topological properties.
Metric space Infographic
 libterm.com
libterm.com